3. Метод ітерацій для рішення рівнянь

Мова йтиме про відшукання корінь рівняння

(3.3.1) ,

т.е. таких чисел , що при підстановці в рівняння замість символу числа виходить тотожність. Саме собою зрозуміло, що тут, як і всюди в цьому курсі, мова йде тільки про речовинні числа.

Відокремити корінь рівняння (3.3.1) - це значить знайти такий інтервал (a,b), що, в перших, містить корінь рівняння (3.3.1) і, по-друге, містить тільки один корінь цього рівняння. Доводиться, що якщо на кінцях деякого інтервалу (a,b) функція має різні знаки, а усередині цього інтервалу похідна знак не міняє, то в інтервалі (a,b) корінь рівняння (3.3.1) є й, притім, тільки один.

Припустимо, що за допомогою тотожних перетворень це рівняння наведене до виду

(3.3.2)

Тоді для довільного числа можна побудувати послідовність чисел Можна довести, що якщо в околиці передбачуваного кореня рівняння (3.3.1), те ця послідовність сходиться саме до цього кореня. Метод ітерацій для рішення рівнянь типу (3.3.1) полягає в тому, що спочатку відділяється корінь рівняння, потім воно перетвориться до виду (3.3.2) із правою частиною, що має похідну по модулі меншу, чим 1, на всьому відрізку, що відокремлює корінь, після чого будується послідовність для довільного з відрізка, у якому відділений корінь.

Процес побудови послідовності треба перервати тоді, коли два рази підряд вийде те саме число із заданим ступенем точності.

Варто спеціально підкреслити, що перетворення рівняння (3.3.1) до виду (3.3.2) з дотриманням умови для похідної є самостійною складною задачею, що вирішують у кожному конкретному випадку заново.

4.4. Метод ітерацій для рішення систем нелінійних алгебраїчних і

трансцендентних рівнянь

Припустимо, що є система рівнянь виду:

.

Її рішення - це будь-який набір чисел такий, що при підстановці в систему c_i замість x_i , i=1,2,...,n, всі рівності стають тотожностями (тобто виходять вираження типу «0=0»). Вирішити систему - це значить знайти всі рішення. Ми це робили поки тільки для частки випадку - коли всі ліві частини - функції лінійні, тобто мають вигляд

причому - константи. Ми шукали рішення систем лінійних рівнянь різними способами, у тому числі - методом ітерацій. У загальному випадку схему ітерацій можна також відтворити. А саме, припустимо, що тотожними перетвореннями дану на початку цього пункту систему рівнянь удалося представити у вигляді:

Тоді, почавши з довільного набору , можна організувати ітерації де . У випадку лінійних систем рівнянь ми повідомляли умови, які повинні виконуватися для того, щоб зазначений процес ітерацій приводив саме до рішення даної системи рівнянь. У загальному випадку такі умови формулюються в істотно більше складних термінах - якобіанах.

Лекция 5 звернення матриць. Подвійність у лінійному програмуванні. Одночасне рішення пари двоїстих задач лінійного програмування.

Зворотна матриця

Нехай А и В - дві матриці наступного виду:

і ;

оборотний увага на те, що в першій з них стовпців стільки ж, скільки в другий з них - рядків. У цьому випадку можна побудувати нову матрицю З

,

називану добутком А на В (пишуть ІЗ=АВ), за правилом

,

де i=1,...,m і j=1,...,r. Серед матриць прийнято виділяти й позначати буквою E

наступну матрицю, називану одиничної, -

;

пояснимо: одинична матриця завжди квадратна, по її діагоналі коштує 1, а всі інші елементи - нулі, тобто якщо Е=(е_ij), i,j=1,...,n, те

.

Говорять, що квадратна матриця А и квадратна матриця В того ж розміру є зворотними по відношенню друг до друга, якщо виконано хоч одне з матричних рівностей - або АВ=Е або ВА=Е. Можна перевірити, що якщо одне із цих матричних рівностей виконується, то виконується й інше. Про всякий випадок пояснимо, що слова «матрична рівність» означають рівність заелементне, тобто якщо має місце рівність матриць U=V, те це означає, що в них рівні кількості рядків і рівні кількості стовпців і при цьому u_ij=v_ij для всіх i і j. Зокрема, система лінійних алгебраїчних рівнянь із п.3 Лекції 1 може бути записана у вигляді AX=B, де

,

а А и В мають той же змив, що й у п.3 Лекції 1.

Неважко помітити, що якщо для квадратної матриці А потрібно знайти зворотну матрицю В, те треба вирішити n систем лінійних алгебраїчних рівнянь із однієї й тої ж матрицею: запишемо матричну рівність АВ=Е поелементно (тут усього вийде n² рівностей), причому будемо послідовно дорівнювати стовпці - перший стовпець лівої частини до першого стовпця правої частини, другий стовпець лівої частини до другого стовпця правої частини й т.д. –

Із цього спостереження треба, що знайти зворотну матрицю можна вирішуючи одночасно n систем лінійних алгебраїчних рівнянь із однієї й тією же матрицею А.

Визначення пари двоїстих задач лінійного програмування.

Нагадаємо, що основна задача лінійного програмування - це задача пошуку максимуму лінійної функції

при обмеженнях

.

Припустимо тепер, що серед тільки що зазначених обмежень присутні точні рівності й для визначеності будемо вважати, що для мають місце неточні рівності, а для - рівності точні:

.

Ясно, що таке припущення не зменшує спільності задачі. Припустимо, далі (і це теж не зменшить спільність задачі), що є невільні невідомі й вільні .

Задачею, двоїстої до ОЗЛП, називається задача пошуку мінімуму лінійної функції

при обмеженнях:

,

,

а також при невільних невідомих , і вільних невідомих . Тут треба звернути увагу, що цільова функція двоїстої задачі виходить із коефіцієнтів, які дорівнюють правим частинам у вихідних обмеженнях, обмеження у двоїстій задачі відповідають стовпцям матриці коефіцієнтів вихідної ОЗЛП, причому обмеження-нерівності відповідають невільним невідомим, а обмеження - рівності відповідають вільним змінним; нарешті, невільні змінні у двоїстій задачі відповідають нерівностям вихідної ОЗЛП, а вільні змінні двоїстої задачі відповідають рівностям вихідної ОЗЛП.

Обидві сформульовані задачі називаються парою двоїстих задач. Про такі пари доводиться наступне принципове положення:

1) існує тоді й тільки тоді, коли існує й при цьому має

місце рівність: ;

2) якщо одна із задач суперечлива, те інша або теж суперечлива, або необмежена;

3) якщо одна із задач необмежена, те інша суперечлива.

Одночасне рішення пари двоїстих задач лінійного програмування.

Неважко помітити, що двоїста задача до основної задачі лінійного програмування сама є задачею лінійного програмування. Як показувалося вище, її можна привести до канонічного виду основної задачі лінійного програмування й, отже, вирішити симплекс-методом. Останній являє собою певні дії з конкретною числовою таблицею.

Якщо зрівняти числову таблицю, використовувану при симплекс-методі для основної задачі лінійного програмування, із числовою таблицею, використовуваної при симплекс-методі для двоїстої задачі, то виявиться, що рішення цих двох задач можна провести одночасно, маніпулюючи з однієї й тією же таблицею. Відтворимо цю таблицю:

		v1=	...	vj=	...	vn=	w=
		-x1	...	-xj	...	-xn	1
u1	y1=	a11	...	a1j	...	a1n	c1
...	...	...	...	...	...	...	...
ui	yi=	ai1	...	ai,j	...	ai,n	ci
...	...	...	...	...	...	...	...
um	ym=	am1	...	am,j	...	am,n	cm
1	z=	-p1	...	-pj	...	-pn	0

Можна помітити, що проведення симплекс-методу із цією таблицею у відношенні змінних x_j, y_i дає рішення й для двоїстої задачі, якщо на кожному кроці міняти місцями й відповідні u_i, v_j. Ми продемонструємо це нижче на конкретному прикладі.

Приклад одночасного рішення пари двоїстих задач лінійного програмування.

Отже, потрібно вирішити одночасно дві екстремальні задачі. Задача перша:

Перш, ніж записати другу задачу, сформуємо стандартну робочу таблицю для пари двоїстих задач, дотримуючись правила з попереднього пункту:

		v1=	v2=	v3=	v4=	w=
		-x1	-x2	-x3	-x4	1
u1	y1=	-3	1	4	1	1
u2	y2=	3	-2	2	-2	-9
u3	0	-2	1	1	3	2
u4	0	-3	2	-3	0	7
1	z=	-10	1	42	54

Тепер по таблиці нам легше буде записати умова двоїстої задачі. А саме:

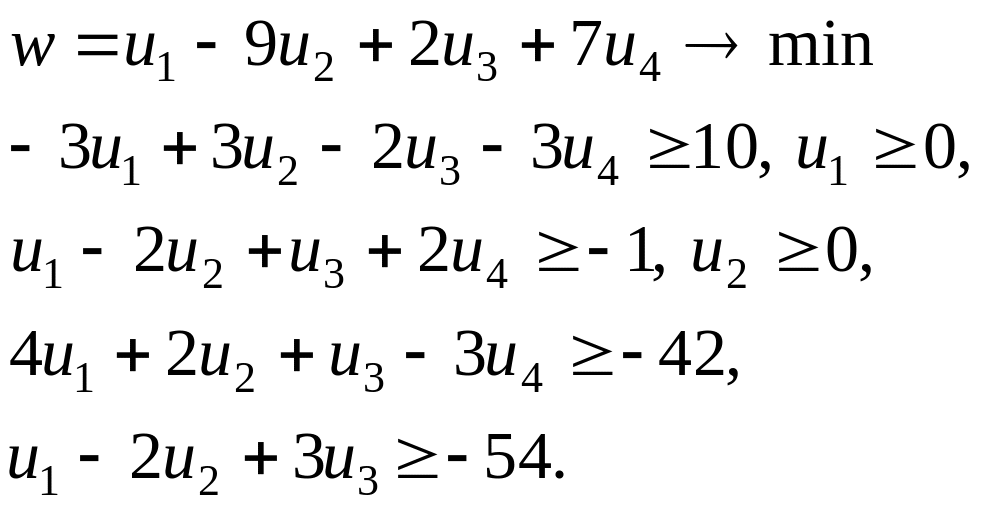
Таким чином, змінні u₃, u₄ - вільні. Алгоритм симплекс-методу нам уже відомий з попереднього викладу; тому будемо лише вказувати розв'язні елементи для чергових модифікованих жордановых виключень (як звичайно, що дозволяє елемент виділяється в таблиці сірим тлом):

		v1=	v2=	v3=	v4=	w=
		-x1	-x2	-x3	-x4	1
u1	y1=	-3	1	4	1	1
u2	y2=	3	-2	2	-2	-9
u3	0	-2	1	1	3	2
u4	0	-3	2	-3	0	7
1	z=	-10	1	42	54

От результат відповідного модифікованого жорданова виключення:

		v1=	u1=	v3=	v4=	w=
		-x1	-y1	-x3	-x4	1
v2	x2=	-3	1	4	1	1
u2	y2=	-3	2	10	0	-7
u3	0	1	-1	-3	2	1
u4	0	3	-2	-11	-2	5
1	z=	-7	-1	38	53	-1

Наступний розв'язний елемент:

		v1=	u1=	v3=	v4=	w=
		-x1	-y1	-x3	-x4	1
v2	x2=	-3	1	4	1	1
u2	y2=	-3	2	10	0	-7
u3	0	1	-1	-3	2	1
u4	0	3	-2	-11	-2	5
1	z=	-7	-1	38	53	-1

Проводимо відповідне модифіковане жорданово виключення:

		u3=	u1=	v3=	v4=	w=
		0	-y1	-x3	-x4	1
v2	x2=	3	-2	-5	7	4
u2	y2=	3	-1	1	6	-4
v1	x1	1	-1	-3	2	1
u4	0	-3	1	-2	-8	2
1	z=	7	-8	17	67	6

Черговий розв'язний елемент:

		u3=	u1=	v3=	v4=	w=
		0	-y1	-x3	-x4	1
v2	x2=	3	-2	-5	7	4
u2	y2=	3	-1	1	6	-4
v1	x1	1	-1	-3	2	1
u4	0	-3	1	-2	-8	2
1	z=	7	-8	17	67	6

Стовпець, що починається з нуля, ураховувати далі, мабуть, не має змісту. Черговий результат:

		u4=	v3=	v4=	w=
		0	-x3	-x4	1
v2	x2=	2	-9	-9	8
u2	y2=	1	-1	-2	-2
v1	x1	1	-5	-6	3
u1	y1=	1	-2	-8	2
1	z=	8	1	3	22

І знову стовпець під нулем не будемо далі враховувати; розв'язний елемент:

		v3=	v4=	w=
		-x3	-x4	1
v2	x2=	-9	-9	8
u2	y2=	-1	-2	-2
v1	x1	-5	-6	3
u1	y1=	-2	-8	2
1	z=	1	3	22

Результат відповідного модифікованого жорданова виключення:

		u2=	v4=	w=
		-y2	-x4	1
v2	x2=	-9	9	26
v3	x3=	-1	2	2
v1	x1	-5	4	13
u1	y1=	-2	-4	6
1	z=	1	1	20

Отже, висновки:

крапка екстремуму для z:

крапка екстремуму для w: