Лекция 2. Геометрическая интерпретация решения задач линейного программирования

План

1. Геометрический смысл задачи линейной оптимизации.

2. Алгоритм графического решения задач ЛП.

1. Пусть дана задача ЛП:

^{Z = c1 x1 + c2 x2 + ⋅⋅⋅ + cn xn → max , (1)}

+ a x + ⋅⋅⋅ + a x ≤ b

^{⎧a11 x1 + a12 x2 + ⋅⋅⋅ + a1n xn ≤ b1}

^⎪

_{⎪a21 x1 22 2 2 n n 2}

^⎨

^{⎪.......................................}

^{⎪⎩am1 x1 + am 2 x2 + ⋅⋅⋅ + amn xn ≤ bm}

(2)

^{x j ≥ 0 ( j = 1, n ). (3)}

^{Рассмотрим систему ограничений (2) с геометрической точки зрения. Ка-}

₂

ждое равенство

^a₁^x₁ ^{+ a}₂ ^x₂ ^{= b}

определяет прямую в пространстве

R . Эта пря-

_{мая делит координатную плоскость на две полуплоскости, определяемые нера-}

венствами

^a₁^x₁ ^{+ a}₂ ^x₂ ^{≤ b}

^{и a}₁^x₁ ^{+ a}₂ ^x₂ ^{≥ b . Данные полуплоскости содержат}

прямую в качестве границы.

₃

Равенство

^a₁^x₁ ^{+ a}₂ ^x₂ ^{+ a}₃ ^x₃ ^{= b}

представляет собой плоскость в

R . Эта

_{плоскость делит пространство на два полупространства, задаваемые неравенст-}

вами

^a₁^x₁ ^{+ a}₂ ^x₂ ^{+ a}₃ ^x₃ ^{≤ b и}

^a₁^x₁ ^{+ a}₂ ^x₂ ^{+ a}₃ ^x₃ ^{≥ b . Граница полупространств –}

_{данная плоскость – принадлежит им.}

По аналогии равенство

^a₁^x₁ ^{+ a}₂ ^x₂ ^{+ ... + a}_n ^x_n ^{= b}

называют гиперплоско-

_{стью в пространстве}

_Rⁿ _{. Это граничная гиперплоскость для полупространств,}

_{определяемых неравенствами. Т.о., система ограничений задачи ЛП (2) содер-}

_{жит m полупространств из пространства}

_Rⁿ _{. Если система совместна (имеет}

хотя бы одно решение), то она определяет выпуклый многогранник, который является геометрическим образом ОДР. Аналогично с трёхмерным пространст- вом будем считать, что угловыми точками выпуклого многогранника в n - мерном пространстве будут его вершины, образованные пересечением гиперп- лоскостей.

Любая внутренняя и граничная точка ОДР является допустимым решени-

ем задачи. Приравняем целевую функцию к нулю. Тогда уравнение

^c₁ ^x₁ ^{+ c}₂ ^x₂ ^{+ ⋅⋅⋅ + c}_n ^x_n ^{= 0}

_{определяет в}

_Rⁿ _{гиперплоскость, проходящую через начало координат и пер-}

пендикулярную вектору-градиенту

^{c = (с}₁^{, с}₂ ^{,..., c}_n ^{) . Направление вектора-}

градиента показывает направление возрастания функции (рис. 1).

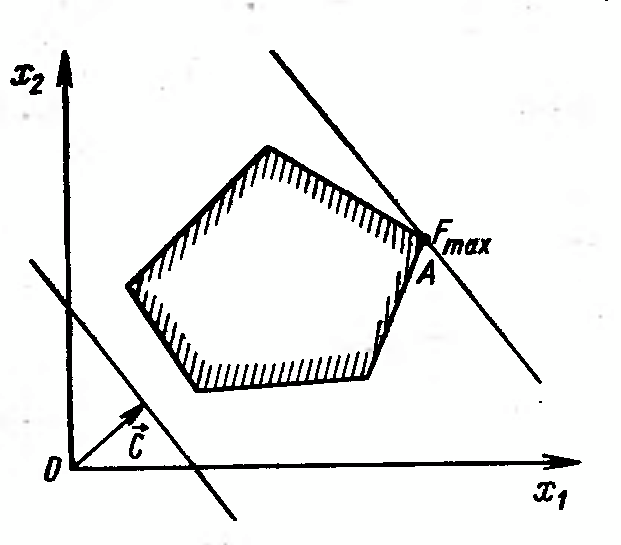
Рис. 1. Графическая иллюстрация задачи ЛП

Поэтому, чтобы найти максимум функции, необходимо передвигать па- раллельными переносами эту гиперплоскость в направлении вектора как можно дальше от начала координат, но чтобы она имела с ОДР хотя бы одну общую точку. Минимум целевой функции достигается в точке ОДР, которая будет ближайшей к началу координат при пересечении с перемещаемой гиперплоско- стью.

2. Пусть задача ЛП содержит только две переменные

^x₁ ^и

^x₂ ^:

^{Z = c1 x1 + c2 x2 → max , (4)}

^⎪ _{+ a x ≤ b}

^{⎧a11 x1 + a12 x2 ≤ b1}

_{⎪a21 x1 22 2 2}

^⎨

^{⎪.......................}

^{⎩⎪am1 x1 + am 2 x2 ≤ bm}

(5)

^{x j ≥ 0 ( j = 1, 2 ). (6)}

^{Тогда все построения можно выполнить в координатной плоскости и решить}

задачу (4)-(6) графически.

_{Приведём алгоритм графического решения задачи ЛП:}

1. Записать уравнения граничных прямых

^а_i1 ^x₁ ^{+ а}_{i 2} ^x₂ ^{= b}_i

^{( i = 1, m ) и построить}

их на плоскости

^x₁^Ox₂ ^.

2. Определить полуплоскости, которые соответствуют каждому ограничению-

неравенству с помощью контрольной точки.

3. Выделить область допустимых решений (ОДР).

4. Построить вектор

_G

^{c = (с}₁ ^,с₂ ⁾

– направление наибольшего возрастания целе-

_{вой функции Z :}

_G

^{c = (с}₁ ^,с₂ ^{) = gradZ}

^{⎛ ∂Z}

⁼ _{⎜ ∂x}

, ^{∂Z ⎞} _.

_⎟

∂x

⎝ 1 2 ⎠

5. Построить прямую, перпендикулярную вектору c . Её называют линией

^{уровня или изоцелью.} _G

6. Перемещать эту прямую в направлении вектора c , если задача на максимум,

и в противоположном направлении, если задача на минимум, пока она не станет касательной (опорной) к ОДР.

7. Определить координаты оптимальной точки и вычислить оптимальное зна-

чение функции Z .

Рассмотрим наиболее типичные ситуации, возникающие при графических решениях задачи ЛП. На рис. 2, А) показано, что в угловой точке A целевая функция достигает максимального значения, а в точке B – минимального.

Рис. 2, Б) отражает случай, когда линия уровня параллельна отрезку AB ,

_{принадлежащему ОДР. Максимум целевой функции достигается в точке A , в}

^{точке B ( Z}_max

^{= Z ( A) = Z (B) ) и в любой точке отрезка AB . Поэтому оптималь-}

ных решений будет бесконечное множество и все они описываются выпуклой комбинацией точек A и B :

^{X * = λ ( x1, A ; x2, A ) + (1 − λ )( x1,B ; x2,B ) = (λ x1, A + (1 − λ ) x1,B ; λ x2, A + (1 − λ ) x2,B ) ,}

^{где 0 ≤ λ ≤ 1.}

А) Б)

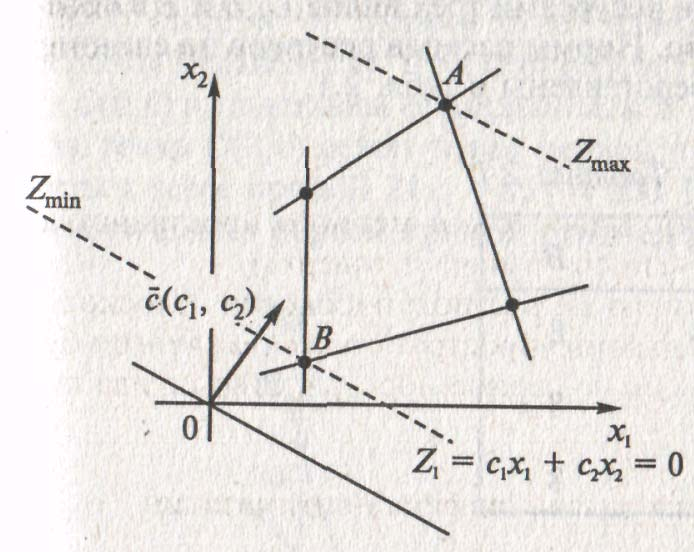
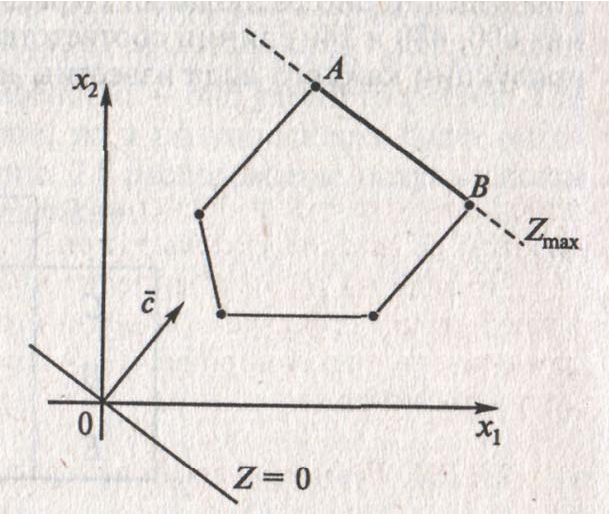
Рис. 2. Наличие графического решения задач ЛП

Напомним, что выпуклой линейной комбинацией произвольных n -

_n

мерных векторов

^X₁ ^{, X} ₂ ^{,..., X} _n

из пространства

R называется сумма

^{λ1 X1 + λ2 X 2 + ... + λn X n ,}

_n

где числа

^{λ j ≥ 0 ( j = 1, n ) и}

^{∑ λ j}

^{j =1}

^{= 1.}

_{Заметим, что в пространстве}

_R2 _{выполняется равенство λ + λ}

_{= 1 . Обо-}

значим вид

^{λ1 = λ , тогда}

1 2

^{λ2 = 1 − λ . Поэтому выпуклая линейная комбинация имеет}

^{λ X}₁ ^{+ (1 − λ ) X} ₂ ^,

^{где 0 ≤ λ ≤ 1.}

^{Принципиально другие ситуации рассмотрены на рис. 3. Так рис. 3, А)}

изображает вариант, когда система ограничений образует неограниченное сверху множество. Функция Z при этом стремится к бесконечности. На рис. 3,

Б) представлен случай несовместной системы ограничений.

А) Б)

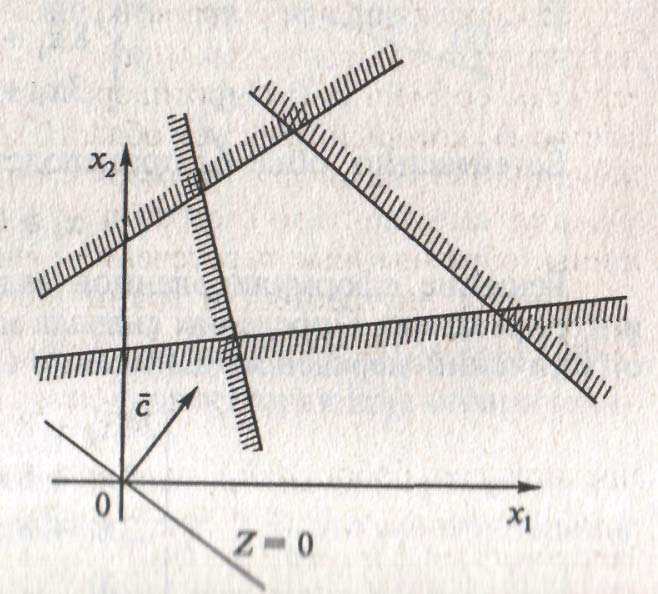
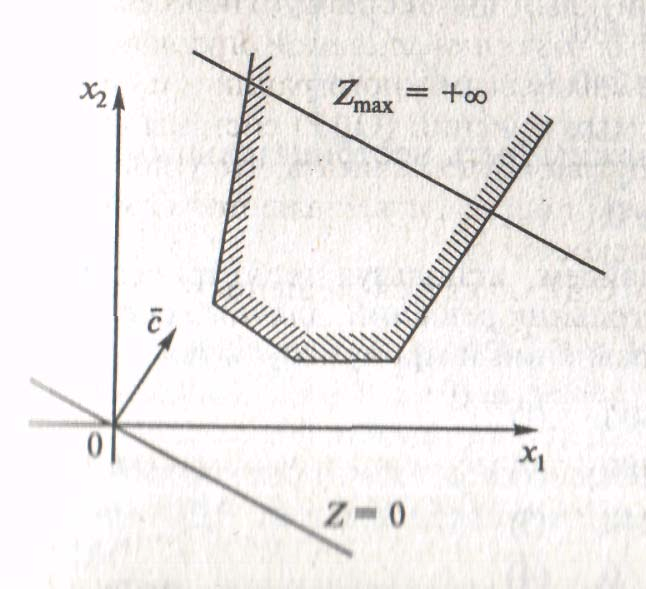
Рис. 3. Случаи отсутствия решения задач ЛП

Домашнее задание. Составить четыре конкретные задачи ЛП на мини-

мум, аналогичные ситуациям, рассмотренным на рис. 2 и 3.