Теорема(о непрерывности сложной функции):
Если:
1)
непрерывна в точке
относительно множества
2)
непрерывна в точке
относительно множества
;
тогда сложная функция
будет непрерывна в точке
относительно множества
.
Свойство 5. Если
непрерывна в точке
относительно множества
,
то модуль
также будет непрерывна в точке
относительно множества
.
Пример:
-непрерывна
тоже.
Свойство 6(непрерывность
результатов арифметических действий
на непрерывных функциях):
Если
и
непрерывны в точке
относительно
,
то их сумма
,
произведение
,
отношение
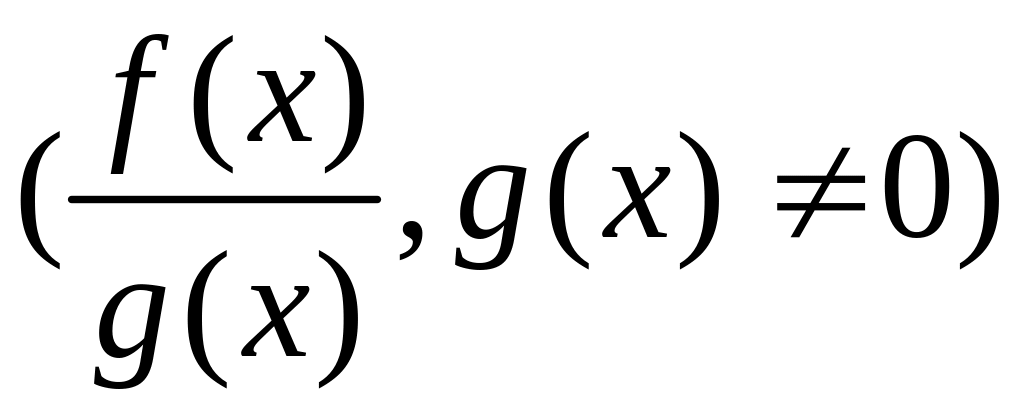будут непрерывны в точке
относительно множества
.
Следствие. Многочлен и дробно-рациональные функции непрерывны во всех точках своей области определения..
- непрерывная функция.
1) - непрерывная функция
2)
- непрерывная функция
3)
-
непрерывная функция
Определение.
Функция
называется непрерывной в точке
относительно
справа(слева), если она непрерывна в
точке
относительно
Пример:
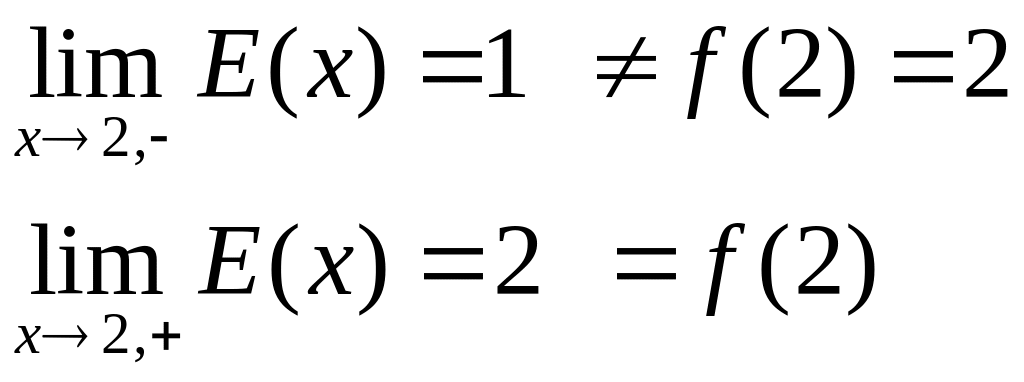
Теорема 1.
.
Пусть
,
тогда для того, чтобы функция
была непрерывна в точке
относительно
необходимо и достаточно, чтобы она была
непрерывно в точке
как слева, так и справа.
Теорема 2(о непрерывной монотонной функции).
Если функция
монотонна на множестве
и
,
то
будет непрерывна во всех
.
Теорема 3(о непрерывности функции обратной к строго монотонной)
Функция, обратная к строго монотонной, определенная на промежутке, является непрерывной во всех точках области определения.
§4.3. Непрерывность элементарных функций.
Основные элементарные функции.
а)
-непрерывна
на всем
.
б)
-непрерывна
на всем
в)
- строго монотонна, область значения
промежутка
.
Следовательно по теореме 2( параграф
4.2,
)
функция будет непрерывна
во всех точках области определения.
г) гиперболические функции
-непрерывные как комбинации непрерывных
функции.
д) тригонометрические функции
Рассмотрим функцию
(см.
док-во первого замечательного предела)
для всех
,
в том числе
при
непрерывность функции доказана.
-
непрерывная функция как комбинация
сложных функций.
-
непрерывна на всех промежутках вида
- непрерывна на всех промежутках вида
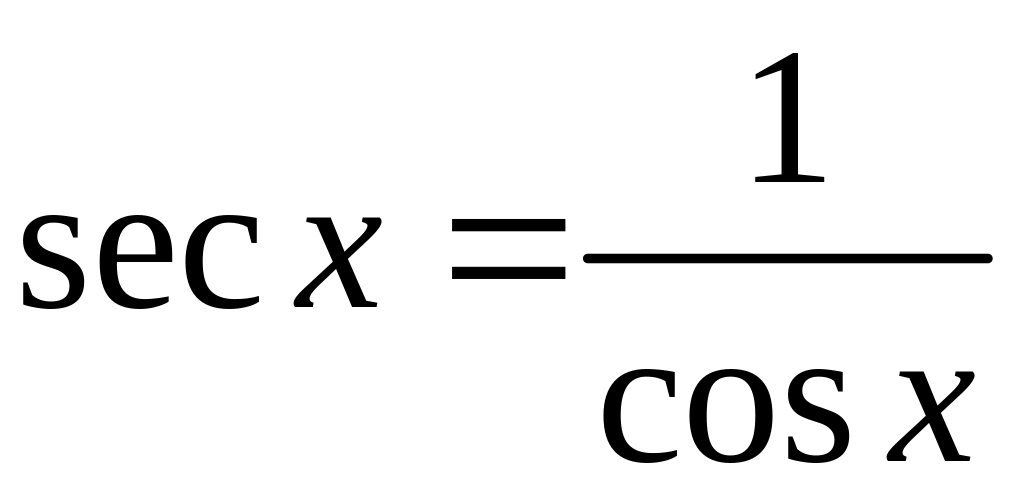- непрерывна на всех промежутках вида
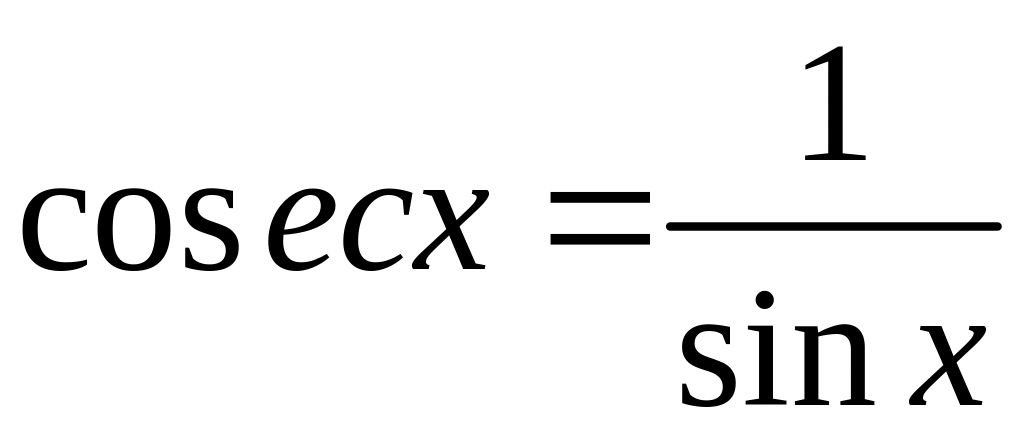- непрерывна на всех промежутках вида
Обратные тригонометрические функции непрерывны по теореме 3 (параграф 4.2.)
§5.2. Основные правила вычисления производной. Теорема (о производной результатов арифметических действий)
Пусть и определены на множестве и имеют в точке конечные производные
Лекция №8.
. Т.к. элементарные функции получаются из основных элементарных с помощью конечного числа арифметических операций и композиций, то все эти функции снова являются непрерывными во всех точках своей области определения.
§4.4. Теоремы Больцано-Коши о промежуточных значениях. Теорема 1.
Если:
1)
непрерывна на
2)
- значения разных знаков,
то
Геометрический смысл: если
непрерывная кривая переходит с одной
стороны оси
на другую, то она пересекает эту ось.
Другого быть не может.
