§5. Производные функции.
§5.1. Понятие производной.
. Задачи, приводящие к понятию производной.
Задача 1. Пусть материальная
точка движется по направляющей прямой
по закону
.
В начальный момент времени
точка находилась в состоянии
.
В момент времени
точка переместилась в положение
.
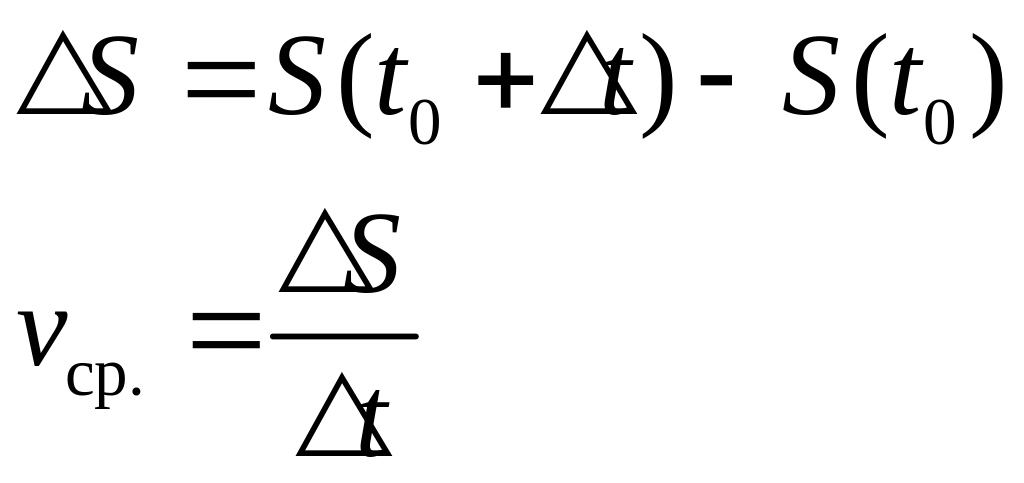
Мгновенной скоростью движения в момент времени называется
(1)
Задача 2 (об угле наклона касательной).
Пусть дана плоская кривая
.
Предельное положение секущей при
называется касательной.
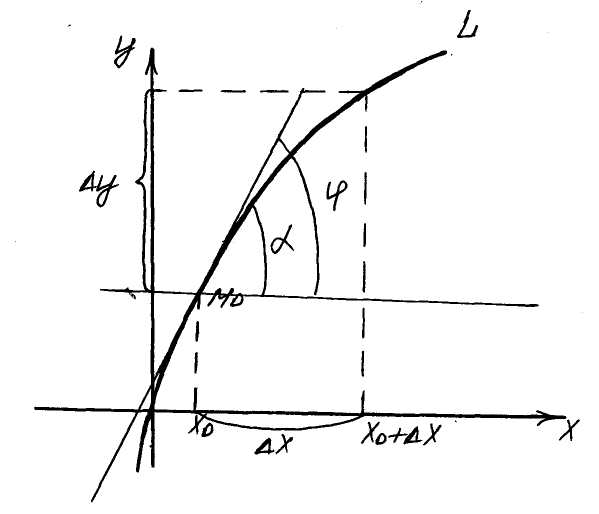
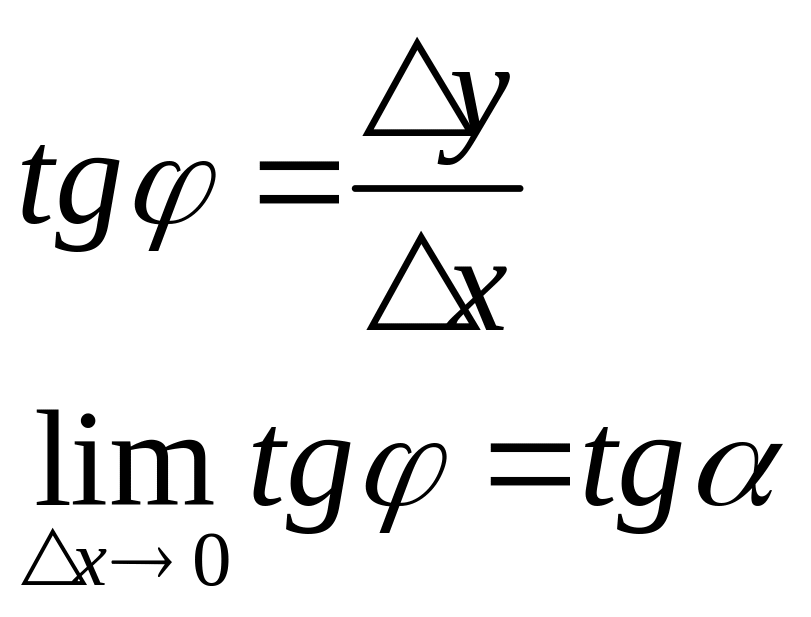
(2)
.
Определение Пусть - функция, определенная на множестве . Производной функции в точке на множестве называется
Формула (1) – механический смысл производной (мгновенная скорость).
Формула (2) – геометрический смысл производной (угол наклона касательной).
. Производная основных элементарных функций.
1)
;
2)
;
рассмотрим
- функция имеет смысл при любых таких
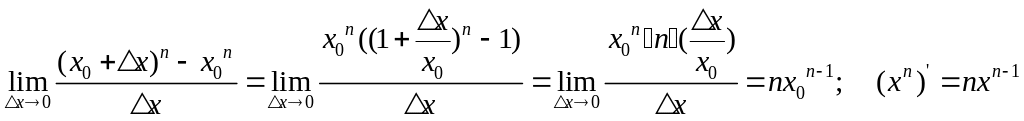
3)
4)
=
5) тригонометрические функции
=
Лекция №9
§5.2. Основные правила вычисления производной Теорема (о производной результатов арифметических действий)
Пусть
и
определены на множестве
и имеют в точке
конечные производные
,тогда:
1)
2)
3)
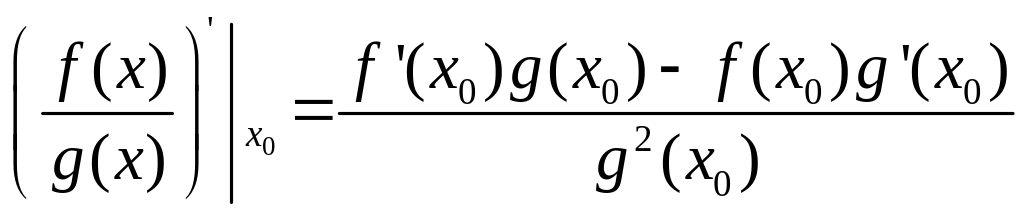
Следствия из теоремы:
Следствие 1:
Следствие2:
Следствие 3: Константу
можно выносить за знак предела
Производные обратной функции.
Теорема.
Если существуют обратные
однозначные к
функции и существует конечная производная
в точке
,а
непрерывна в точке
,
то существует производная обратной
функции в точке
равная
(1).
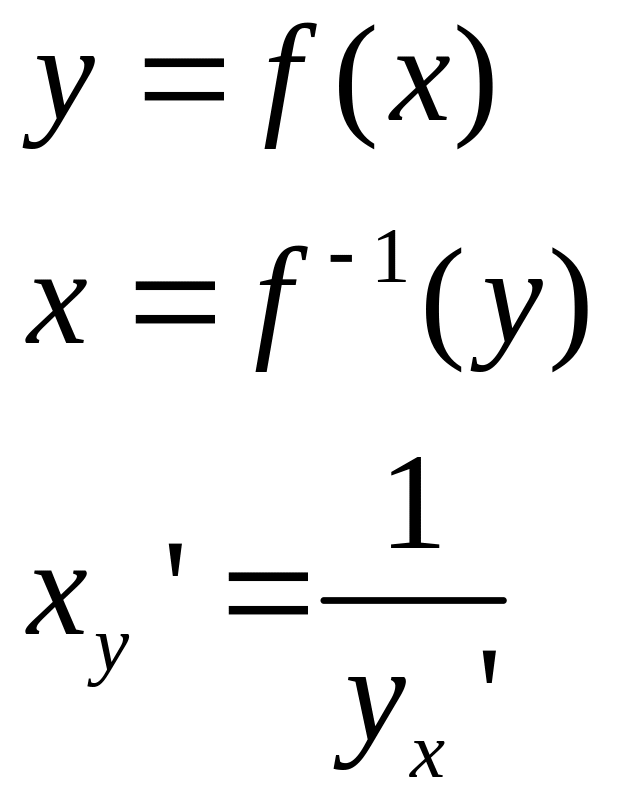
Геометрический смысл теоремы:
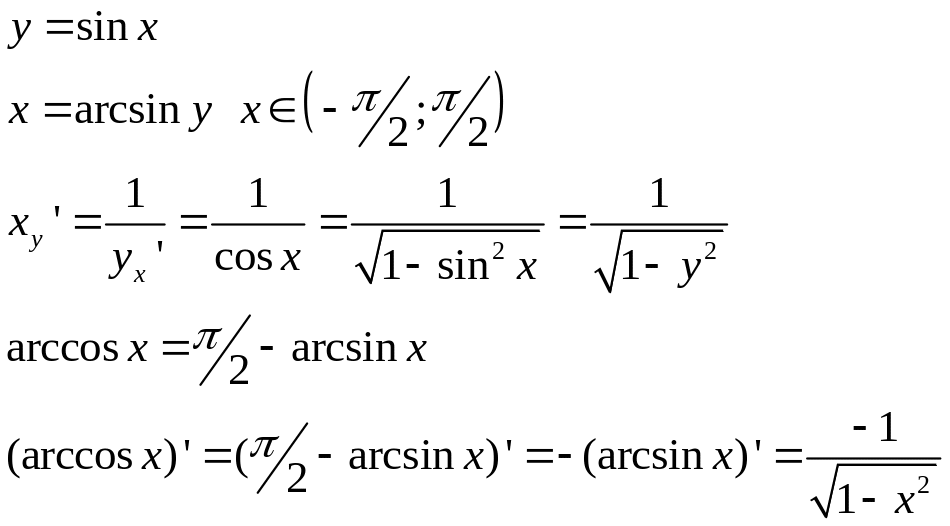
Производная сложной функции.
Теорема.
Пусть
1)
2)
конечные производные
и
тогда
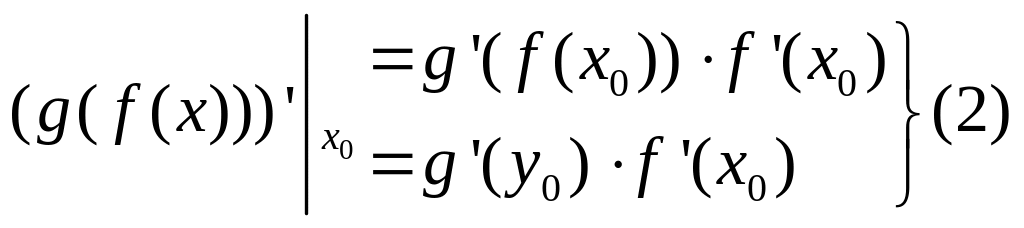
Пример:
§5.3. Связь между существованием производной и касательной.
а) Если
в точке
существует наклонная касательная к
графику функции
,
то в этой точке существует конечная
производная
(параграф 5.1.,задача 2)
б) Докажем, что если существует
,
то существует касательная в этой точке
(
)
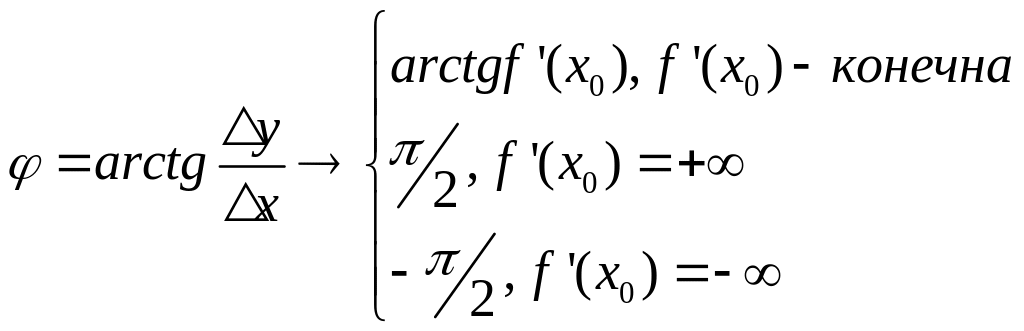,т.е
в любом случае касательная в точке
существует
в) Существование наклонной касательной
в точке
равносильно существованию конечной
производной в точке
.
В пункте б) показано, что существование
производной влечет существование
касательной, причем, если
бесконечна, то касательная вертикальна
( параллельна оси
)
Замечаем, что из существования касательной еще не следует существование производной. С учетом пункта а) это относится к случаю вертикальной касательной.
Пример:
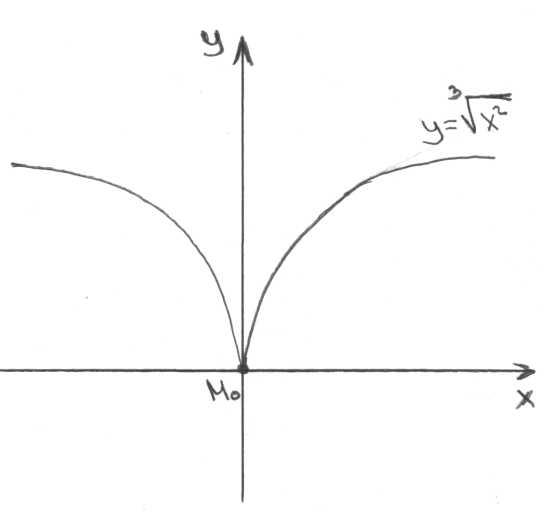
Односторонние пределы и производные.
Определение 1 Предельное
положение секущей при
называется правой (левой) касательной
к графику функции
.
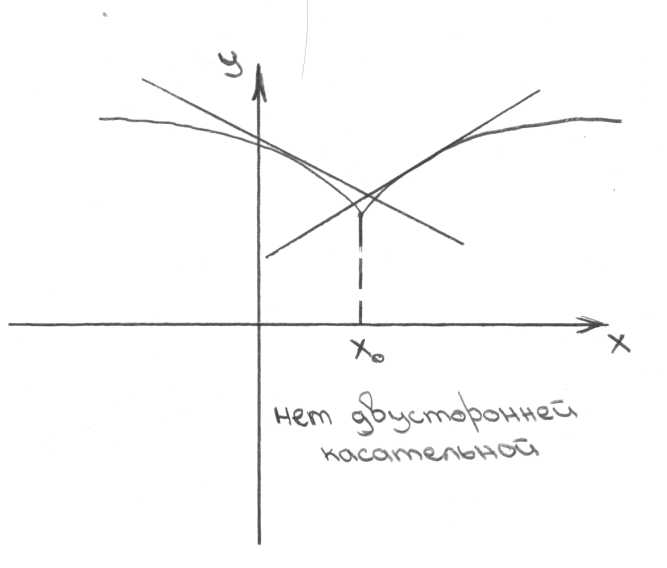
Существование двусторонней производной равносильно существованию и совпадению обеих односторонних производных. Связь между существованием производной и касательной с одной стороны остается прежней.
Односторонняя производная всегда существует. Двусторонняя не всегда.