§3.3. Основные свойства предела.
Свойство 1.
Если
,
то для
.
Свойство 2. Предел функции единственный.
Доказательство:
Пусть функция при имеет два значения предела.
По свойству 3(определимости)
и
:
.
Согласно определению предела (1)
для
,
что как только
Согласно определению предела
(2)
для
Следовательно, если
,
то
,
получаем противоречие.
Сужение функции.
Пусть
Определение. Функция
называется сужением функции
на множестве
,
если
и
для
Свойство 3.
Если:
1)
.
2)
сужение
на
.
3)
.
то,
.
Доказательство:
Для
(*).
и
тем более выполняется условие (*)
.
. Ограниченная функция.
Определение 1. Функция
называется ограниченной сверху (снизу,
просто ограниченной), если множество
её значений ограничено сверху (снизу,
просто ограничено).
Пример:
,
-
ограничена снизу
Определение 2. Функция
называется ограниченной сверху (снизу,
вообще на
),
при
,
если множество её значений ограничено
сверху (снизу, вообще на
)
при
.
Свойство 4. Если существует конечный предел при на , то функция ограничена при на .
Доказательство:
, т.е.
функция
ограничена,
-конечное
число.
Лекция № 4.
.
Предел последовательности.
Последовательность – частный случай функции.
Определение. Последовательность - множество чисел, перенумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров. В роли аргумента – номер члена последовательности.
Определение (предел
последовательности). Число
p называется
пределом последовательности
,
если для всех достаточно больших значений
соответственные значения
становятся как угодно близкими к числу
p, т. е. p=
.
Свойство 5.
Всякая последовательность, имеющая конечный предел, ограничена.
Доказательство:
,
т. е.
Пусть A=min{a,
};
B=max{b, }
Тогда
последовательность
ограничена
Свойство 6 (предел сложной функции).
Пусть выполнено условие:
1)
;
2)
и
;
3) если
,
то
Тогда
или
(1)
Рассмотрим пример, показывающий, что при несоблюдении условия 3) применение формулы (1) может оказаться ошибочным.
Теперь вычислим формально по формуле (1)
Получили неверный результат, т. к. не
выполнено условие 3) в свойстве 6,
ведь
является значением функции f(x)
на
,
между тем
Следствие 1. Если
,
то для любой последовательности
Доказательство:
по формуле (1)
Условие 3) свойства 6 здесь выполнено, т. к. предел внутренней функции не является её значением.
Следствие 2. Если
,
то для любой последовательности
при любом выборе
.
Доказательство:
является сужением функции, поэтому по
свойству 3 она имеет тот же предел,
что и сама функция.
Следствия 1,2 часто используют для доказательства отсутствия пределов.
Например:
при
1)
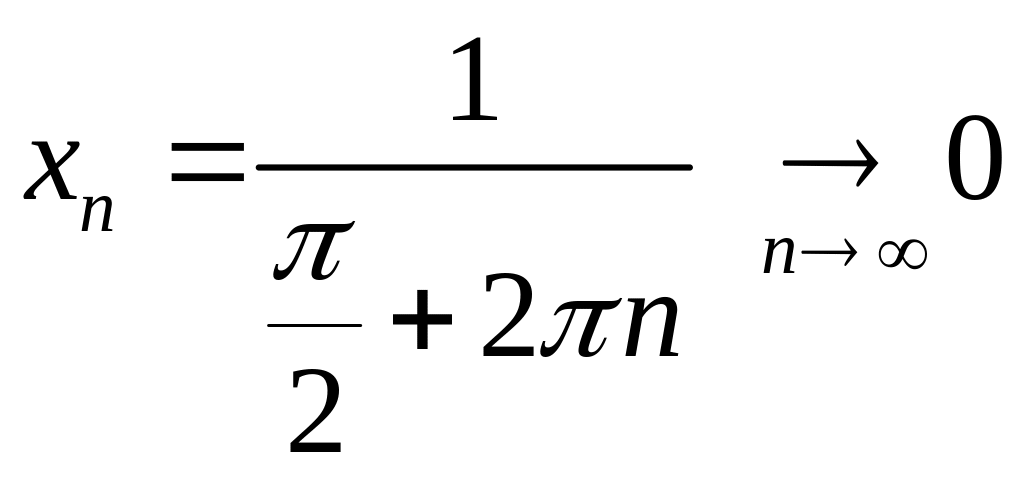
2)
Предела не существует, т.к. он всегда разный.
§3.4. Бесконечно малые и бесконечно большие функции.
. Бесконечно малые функции (бмф).
Пусть
Определение 1 Функция
называется бмф при
,
если
Например:
при
- бмф.
Определение 2 Функция
называется бмф при
,
если для
.