§2.6. Классификация функций.

Функции подразделяются на:

1. Однозначные и многозначные;

2. Явные и неявные;

3. Элементарные и неэлементарные.

Элементарные функции – функции, которые получаются из основных элементов с помощью конечного числа последовательно-выполненных арифметических операций и композиций.

Неэлементарные функции – функции, которые нельзя выразить формулой.

S=1,2,3…n, т.к. её нельзя выразить с помощью конечного числа последовательно-выполненных арифметических операций и композиций.

S=1+2+3+…+n=

В классе элементарных функций выделяют:

1. Алгебраические функции:

а) Рациональные функции. Получены с помощью арифметических операций +,-,*;

б) Дробно-рациональные функции. При их образовании участвуют +,-,*,/;

в) Иррациональные функции. Добавляется .

2. Трансцендентными называются все элементарные функции, не являющиеся алгебраическими.

sin, cos, log, ln…

Лекция №3.

§3. Предел функции.

§3.1. Окрестности.

Пусть - действительное число .

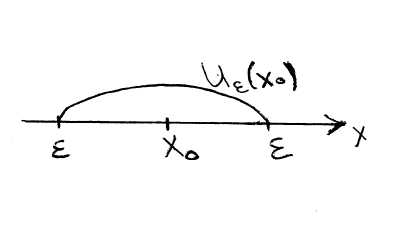
Определение1. окрестности точки называется отрезок вида .

Определение2. окрестности точки называется отрезок .

Определение 3. Окрестностью точки называется любой отрезок, содержащий некоторую окрестность этой точки.

Свойства окрестностей:

Свойство 1. Для ,содержащая саму эту точку .

Свойство 2. пересечение двух окрестностей точки снова является окрестность этой точки.

Доказательство:

Рассмотрим её окрестности и . .

Тогда пересечение исходных , где

Свойство 3(определимость). Если , , причем , то существует окрестности и , такие что .

Доказательство:

Если , то одна из них больше другой. Допустим .

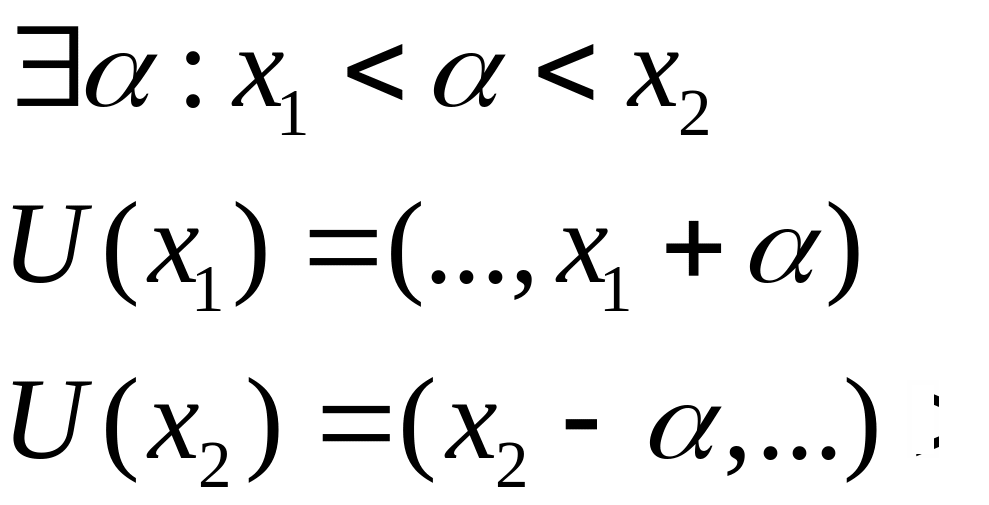
Предельная точка множества.

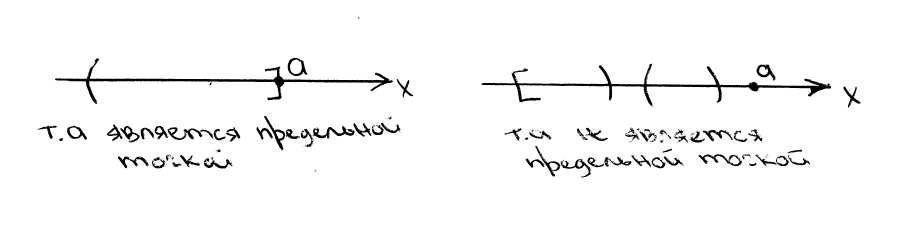
Определение. Точка называется предельной для некоторого множества , если в любой её окрестности существует хотя бы одна точка из , отличная от .

Теорема.

В любой окрестности предельной точки содержится бесконечное количество точек множества .

Доказательство:

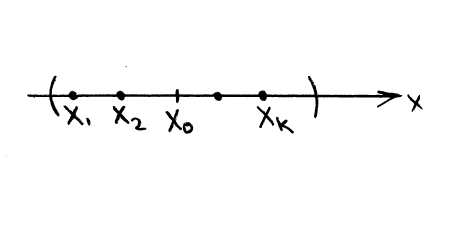
-конечное число точек

Существует , которая не содержит

Существует , которая не содержит

Существует , которая не содержит

Пересечение двух, а значит и конечного числа окрестностей снова является окрестностью, а значит

Таким образом мы построили , которое не содержит ни одной точки из , что противоречит тому, что -предельная точка.

§3.2. Определение предела функции.

Определение 0. Число называется пределом функции при , если значение функции становится как угодно близким к числу , как только становится достаточно близким к .

Определение 1. Пусть функция , . Число называется пределом ( ), если для , такая что, как только попадает в эту окрестность ( )

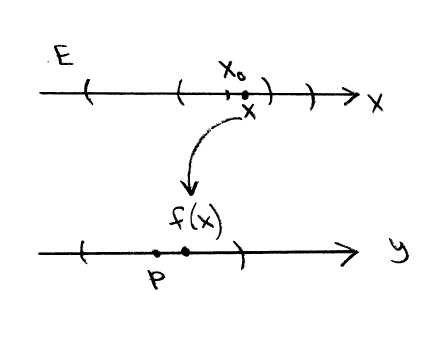
Определение 2. Число называется функции , если для существует , такая что .

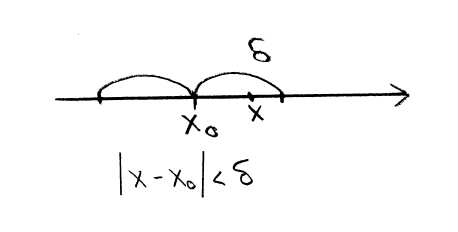
Зная, что такое и окрестности точки, можно дать определение с точки зрения неравенств.

Пусть (конечные точки). Тогда , если для

Пусть .

Тогда .