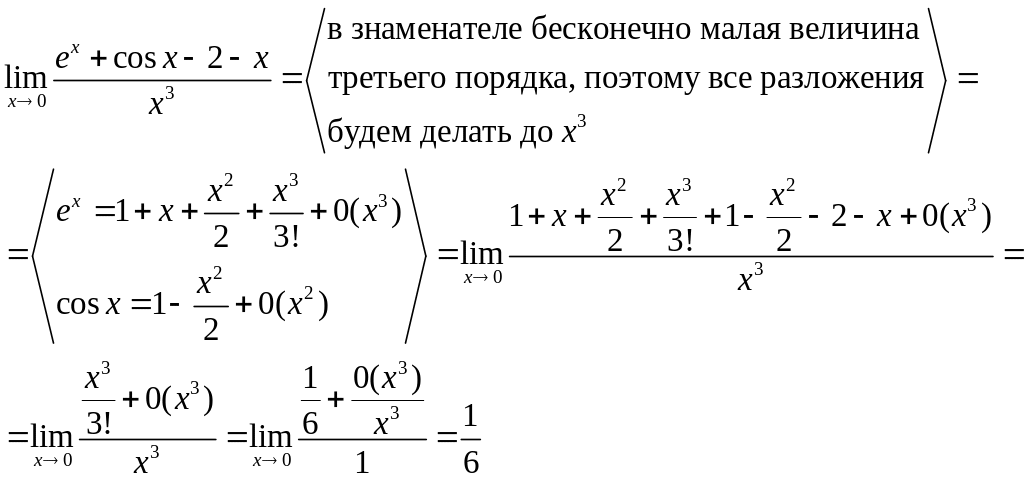- •Лекция №1.
- •§1. Множество вещественных чисел.
- •§1.1. Понятие вещественного числа и числовая ось.
- •§1.2. Граница числовых множеств.
- •§1.3. Абсолютная величина числа.
- •§1.4. Числовая ось.
- •§2. Функции
- •§2.1. Понятие функции.
- •§2.2. График функции.
- •Лекция № 2.
- •§2.3.Обратная функция.
- •§2.4. Композиция функции.
- •§2.5. Основные элементарные функции.
- •§2.6. Классификация функций.
- •§3. Предел функции.
- •§3.1. Окрестности.
- •Теорема.
- •§3.2. Определение предела функции.
- •§3.3. Основные свойства предела.
- •§3.4. Бесконечно малые и бесконечно большие функции.
- •Теорема.
- •§3.5. Пределы результатов арифметических действий. Теорема.
- •§3.6. Односторонние пределы.
- •§3.7. Свойство предела в области значений функции. Теорема 1.
- •Теорема 2.
- •§3.8.Сравнение функции при на .
- •§3.9. Число е.
- •Теорема 1.
- •Теорема 2.
- •§3.10. Лемма о вложенных промежутках.
- •Лемма (Коши-Кантора).
- •§3.11. Лемма (Больцано-Вейерштрасса) о выделении сходящейся последовательности.
- •Лемма (Больцано-Вейерштрасса).
- •§3.12. Критерий Больцано-Коши сходимости последовательности.
- •Теорема (критерий Больцано-Коши).
- •Теорема 2 (критерий Больцано-Коши: существования конечного предела функции).
- •§3.13. Некоторые эквивалентности и формулы полезные при вычислении пределов.
- •§4. Непрерывные функции.
- •§4.1. Понятие непрерывной функции.
- •§4.2. Свойства непрерывной функции.
- •Теорема(о непрерывности сложной функции):
- •Теорема 1.
- •Теорема 2(о непрерывной монотонной функции).
- •Теорема 3(о непрерывности функции обратной к строго монотонной)
- •§4.3. Непрерывность элементарных функций.
- •§5.2. Основные правила вычисления производной. Теорема (о производной результатов арифметических действий)
- •§4.4. Теоремы Больцано-Коши о промежуточных значениях. Теорема 1.
- •Теорема 2.
- •§4.5. Открытые и замкнутые множества.
- •Теорема (критерий открытости и замкнутости множеств).
- •§4.6. Компакты.
- •Теорема (критерий компакта).
- •Теорема Вейерштрасса о непрерывных функциях.
- •§4.7. Классификация разрывов функции.
- •§5. Производные функции.
- •§5.1. Понятие производной.
- •§5.2. Основные правила вычисления производной Теорема (о производной результатов арифметических действий)
- •Теорема.
- •Теорема.
- •§5.3. Связь между существованием производной и касательной.
- •§5.4. Понятие дифференциалов функции.
- •Теорема
- •§5.5. Основные формулы и правила вычисления дифференциала.
- •Теорема.
- •Теорема.
- •§5.6. Использование дифференциала для приближенных вычислений.
- •§5.7. Производные высших порядков (в.П.).
- •§5.8. Дифференциалы высших порядков (в.П.).
- •§4. Основные теоремы дифференциального исчисления.
- •§4.1. Теорема Ферма.
- •Теорема Ферма(о нуле производной).
- •§6.2. Теорема Роля Теорема Роля
- •§6.3. Теорема Лагранжа. Теорема.
- •§6.4. Теорема Коши о конечных приращениях. Теорема.
- •§6.5. Формула Тейлора.
- •§6.6. Приложение формулы Тейлора.
- •§6.7. Правило Лапиталя. Теорема (правило Лапиталя-Бернулли).
- •§7. Исследование функции с помощью производной.
- •§7.1. Признаки монотонности и постоянства функции. Теорема 1.
- •Теорема 2.
- •Теорема 3(необходимый признак монотонности)
- •§7.2. Экстремум функции.
- •Теорема.
- •Теорема 1(первый достаточный признак)
- •Теорема 2 (второй достаточный признак экстремума)
- •§7.3. Нахождение наибольшего и наименьшего значений функции.
- •§7.4. Направление вогнутости и точки перегиба графика функции.
- •§7.5. Асимптоты к графику функции.
- •Теорема (критерий наклонной асимптоты).
- •§7.6. Построение графика функции с использованием производных.
§6.3. Теорема Лагранжа. Теорема.
Если:
1) непрерывна на
2) в
тогда существует точка
![]() (1)
(1)
Теорема Роля является частным случаем
теоремы Лагранжа, т.к.
![]() ,
тогда
.
,
тогда
.
Геометрический смысл:
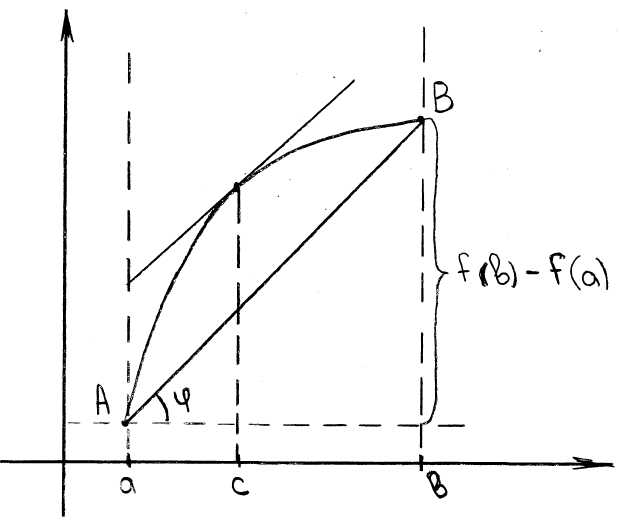
![]()
![]() геометрически означает, что угол наклона
касательной в точке
равен углу наклона хорды
геометрически означает, что угол наклона
касательной в точке
равен углу наклона хорды
![]() .
.
Формулу (1) называют формулой конечных
приращений Лагранжа и записывают в
виде:
![]() (1)
(1)
§6.4. Теорема Коши о конечных приращениях. Теорема.
Пусть функция и :
непрерывны в
имеют конечные производные
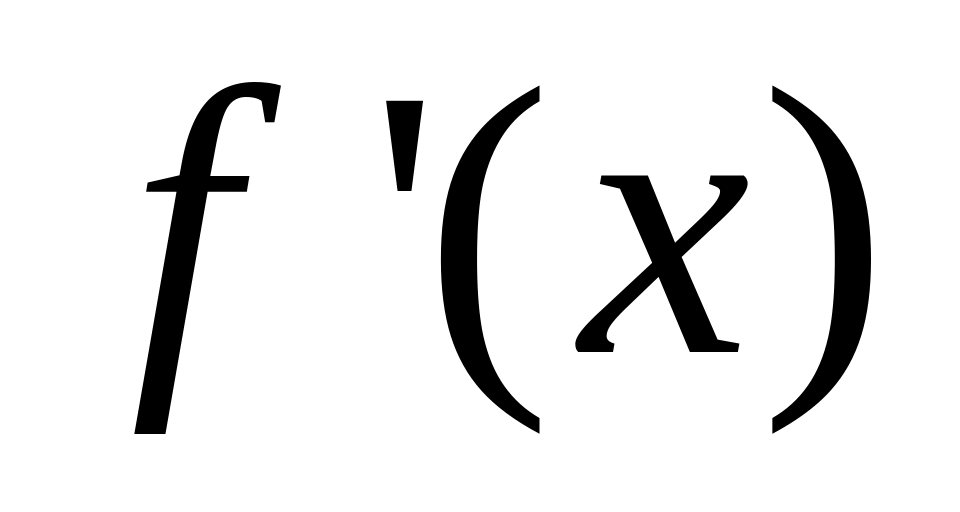 и
и
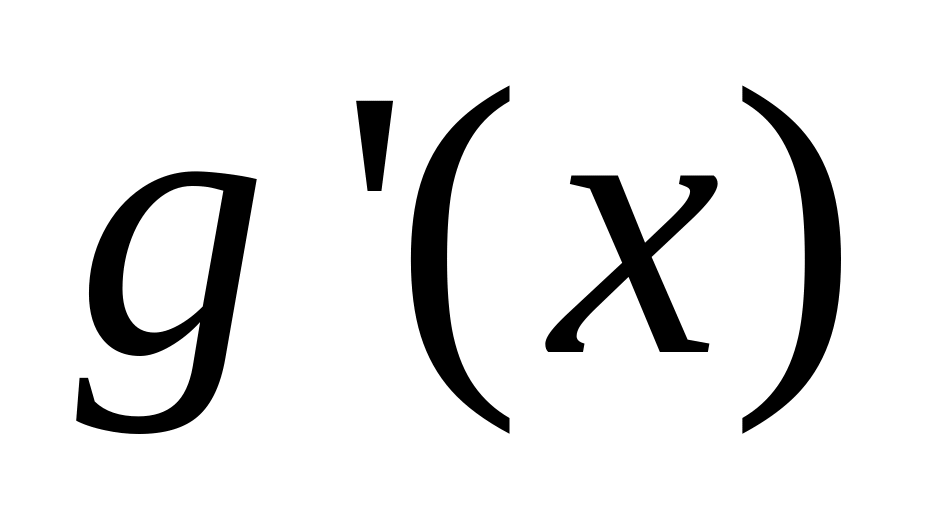 в
в
и конечна
тогда существует точка
![]() (1)
(1)
Теорема Лагранжа – это частный случай
теоремы Коши, которая получается, если
![]() .
.
Доказательство:
а) сначала покажем, что
![]() ,
т.е.
,
т.е.
![]() .
Если допустить противное:
.
Если допустить противное:
![]() ,
то функция
удовлетворяет условиям теоремы Роля
,
то функция
удовлетворяет условиям теоремы Роля
![]() ,
а это противоречит условию (3)
,
а это противоречит условию (3)
б) введем вспомогательную функцию
![]() Утверждается, что данная функция
удовлетворяет условиям теоремы Роля
Утверждается, что данная функция
удовлетворяет условиям теоремы Роля
![]()
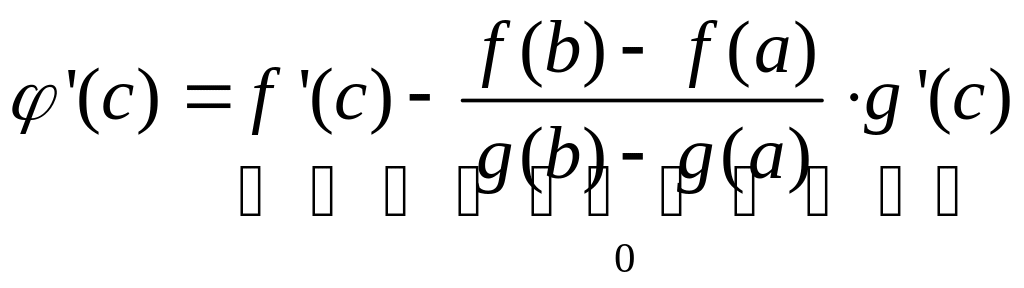 ,
т.е. получена формула (1)
,
т.е. получена формула (1)
В литературе все рассмотренные теоремы: Ферма, Роля, Лагранжа и Коши – называются теоремами о среднем.
§6.5. Формула Тейлора.
Для многочленов.
Любой многочлен
-ной
степени можно записать в следующем
виде:
![]() (1). Возьмем
(1). Возьмем
![]() .
Многочлен вида (1) можно записать по
степеням
.
Многочлен вида (1) можно записать по
степеням
![]() .
Для этого
.
Для этого
![]()
![]()
(по биному Ньютона
![]()
![]()
![]() )
)
Группируемпо степеням и получаем, что
многочлен:
![]() (1’)
(1’)
Для определения коэффициентов
![]() положим в формуле (1’) такое условие,
что
положим в формуле (1’) такое условие,
что
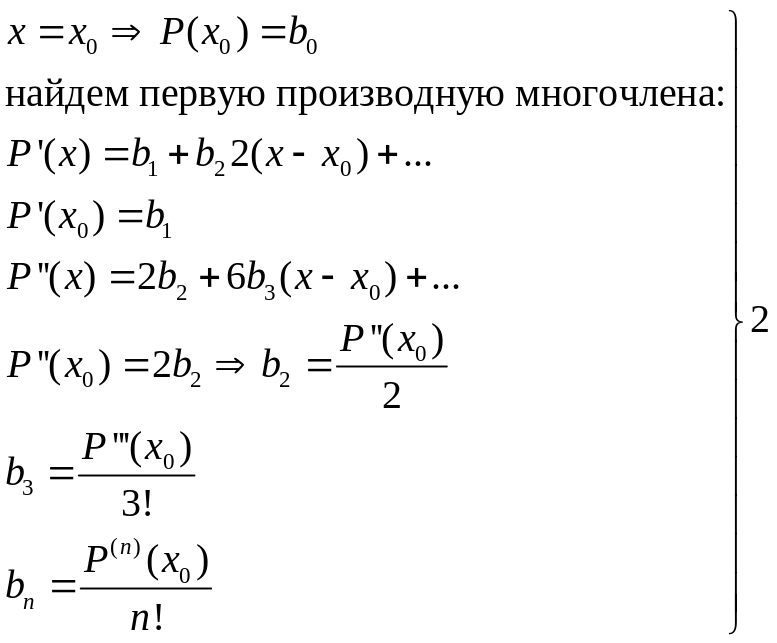
Таким образом, с учетом полученных
формул (2) формулу (1’) можно переписать
в следующем виде :
![]() (1’’).
(1’’).
Формула (1’’) – это формула Тейлора для многочлена -ной степени.
Замечание: Если многочлен записан
в виде (1’) по степеням
,
то его коэффициенты выражаются по
формуле
![]() (3), по которой можно сказать, что
вычисляются коэффициенты по известным
производным и наоборот. Поэтому, если
многочлен записан в виде
(3), по которой можно сказать, что
вычисляются коэффициенты по известным
производным и наоборот. Поэтому, если
многочлен записан в виде
![]() ,
то ясно, что все производные в точке
равны соответственно
,
то ясно, что все производные в точке
равны соответственно
![]()
.Для функций.
Рассмотрим функцию , которая точке имеет все необходимые производные.
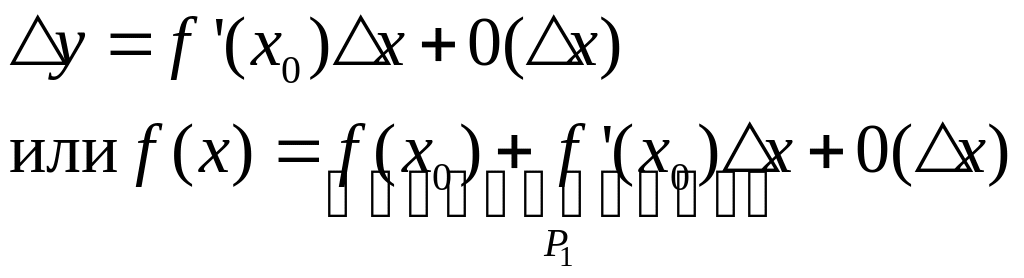
Многочлен
![]() дает приближение функции на величину
дает приближение функции на величину
![]() .
Многочлен
обладает свойством , что его значение
в точке
и первая производная в точке
совпадают с таковыми для самой функции.
Возникает гипотеза, что многочлен
-ного
порядка
.
Многочлен
обладает свойством , что его значение
в точке
и первая производная в точке
совпадают с таковыми для самой функции.
Возникает гипотеза, что многочлен
-ного
порядка
![]() даст еще большее приближение нашей
функции, причем значение этого многочлена
и его производной в точке
совпадает с таковыми для самой функции.
даст еще большее приближение нашей
функции, причем значение этого многочлена
и его производной в точке
совпадает с таковыми для самой функции.
![]() (4) – многочлен Тейлора
-ной
степени для функции
с центром в точке
.
(4) – многочлен Тейлора
-ной
степени для функции
с центром в точке
.
Обозначая
![]() ,
можно записать:
,
можно записать:
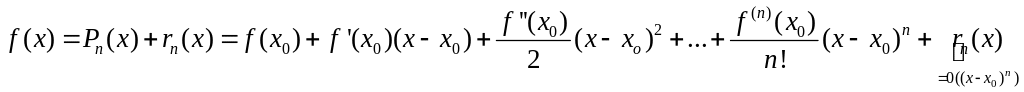 (5)-
формула Тейлора
-ной
степени для функции
с центром в точке
и остаточным членом
(5)-
формула Тейлора
-ной
степени для функции
с центром в точке
и остаточным членом
![]() .
.
Замечание. Записывая
![]() ,
говорят, что остаточный член записан в
форме Пеано. Формула Тейлора для функции
при
,
говорят, что остаточный член записан в
форме Пеано. Формула Тейлора для функции
при
![]() называют формулой Маклорена:
называют формулой Маклорена:
![]()
Лекция №12.
§6.6. Приложение формулы Тейлора.
Для разложения некоторых функций (все разложения будут рассматриваться по формуле Маклорана, т.е. при ).
1)
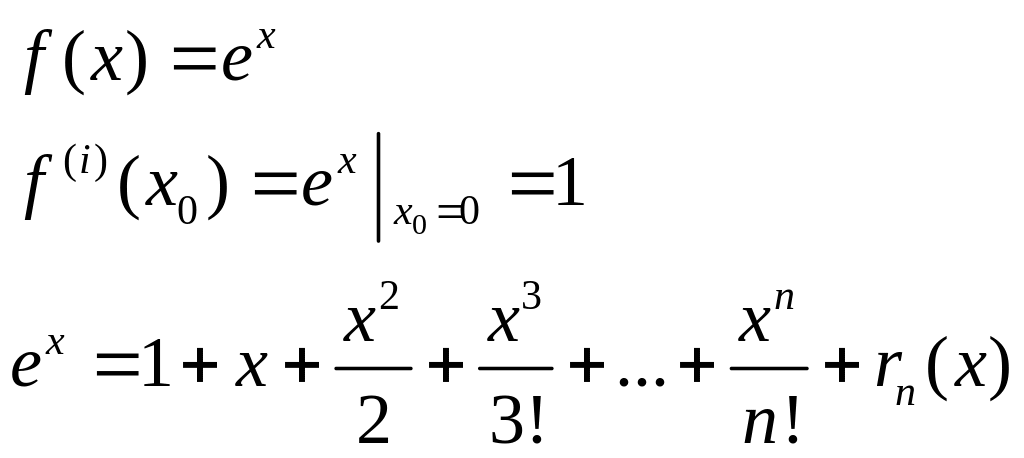
2)
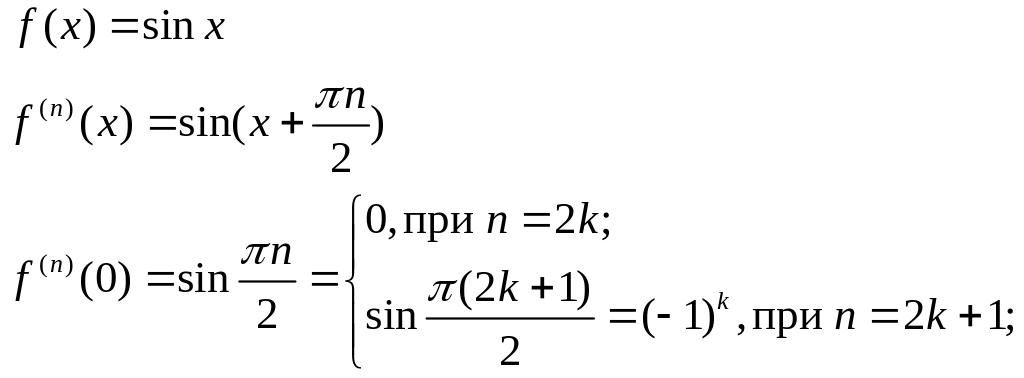
В разложении будут отсутствовать четные номера производных, а нечетные будут чередоваться, начиная с +1.
![]()
3)
![]()
В разложении будут отсутствовать нечетные номера, а четные будут чередоваться, начиная с +1.
![]()
4)
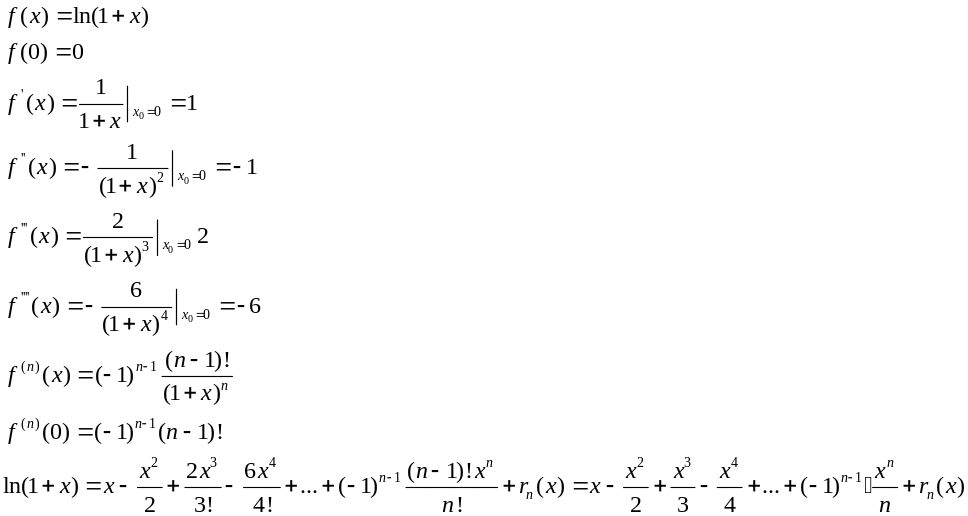
5) Биноминальное разложение
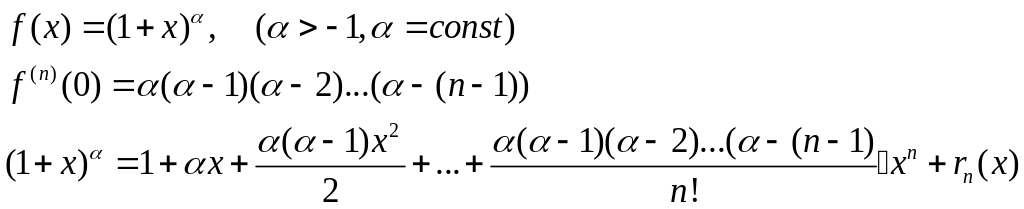
Если
в полученных формулах взять в виде
![]() (в форме Пиана), то увидим, что все они
дают нам более точные, чем известные
нам ранее выражения эквивалентности
для функций
(в форме Пиана), то увидим, что все они
дают нам более точные, чем известные
нам ранее выражения эквивалентности
для функций
![]() ,
приближения.
,
приближения.
Для вычисления некоторых функций.
При разложении формул Тейлора можно оценить погрешность этой формулы, т.л. она равна (по абсолютной величине) первому отброшенному члену.
Например:
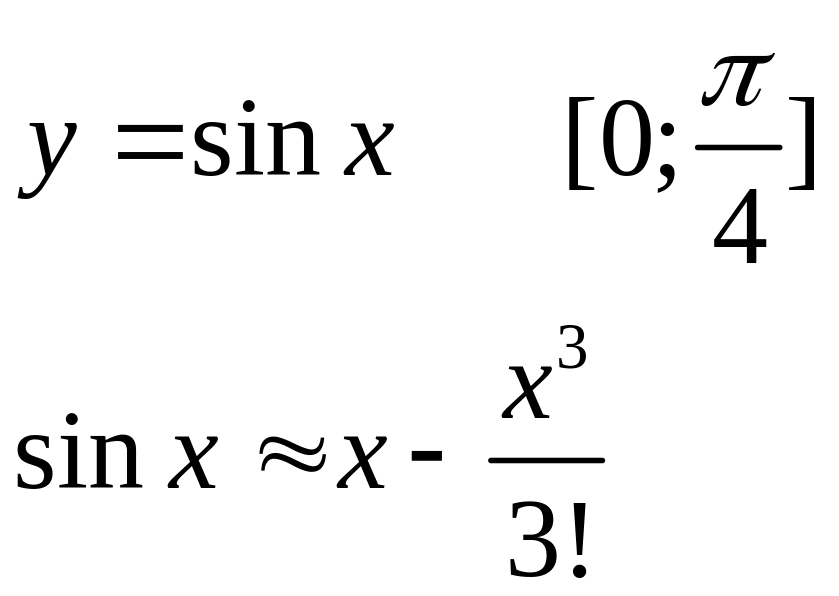
определяем погрешность
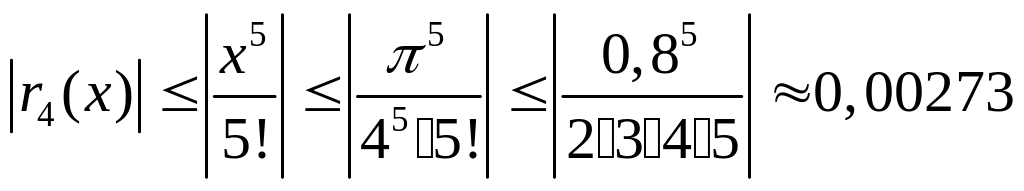
Для вычисления пределов.