§5.4. Понятие дифференциалов функции.

Определение 1 Функция называется дифференцируемой в точке , если её приращение можно представить в виде: 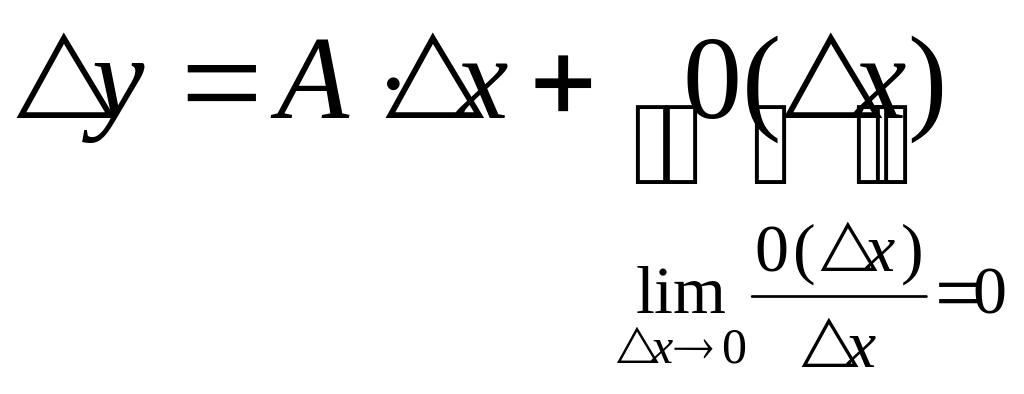при (1)

А-число, конечная константа.

В формуле (1) слагаемое линейно относительно и дает основную часть приращения функции. Это слагаемое отличается от на бесконечно малую величину .

Поэтому его называют главной линейной частью приращения функции.

Определение 2 Если функция дифференцируема в точке , то главную линейную часть приращения функции в этой точке называют дифференциалом функции в точке с приращением аргумента . Обозначают дифференциал

Теорема

Утверждение, что дифференцируема в точке равносильно утверждению, что существует конечная , при этом в формуле (1) . С учетом теоремы дифференциал функции записываем:

Доказательство:

Функция дифференцируема в точке .

Тогда

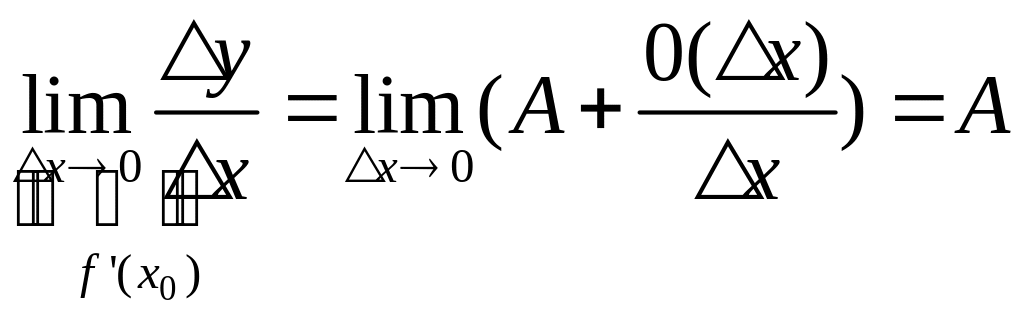
Приращение аргумента обычно называют дифференциалом и обозначают , поэтому окончательно для дифференцирования функции имеем такой вид: (2)

Замечание.

1. Из формулы (2) следует, что .

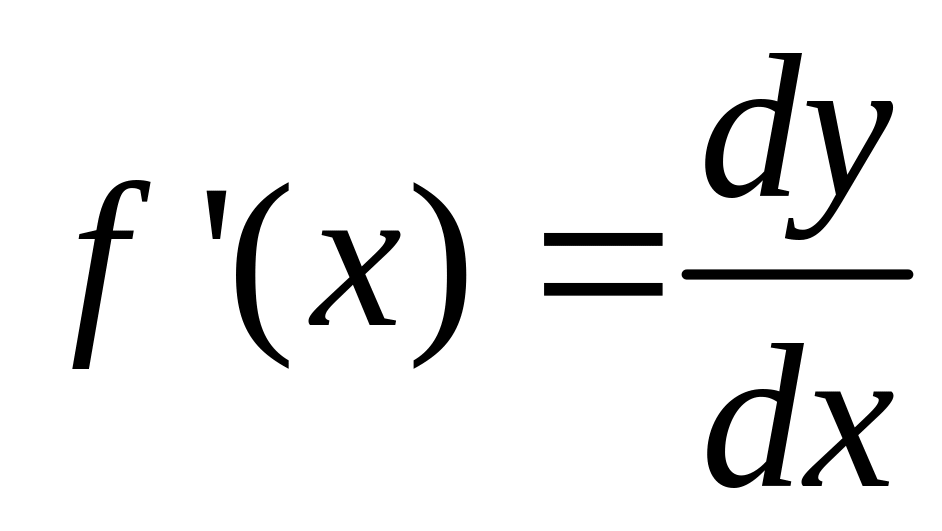2. Так как дифференцируемость функции эквивалентна существованию конечной производной, то часто вместо того, чтобы сказать второе, говорят первое, и наоборот. Процесс нахождения производной называют дифференцированием.

Геометрический смысл дифференциала.

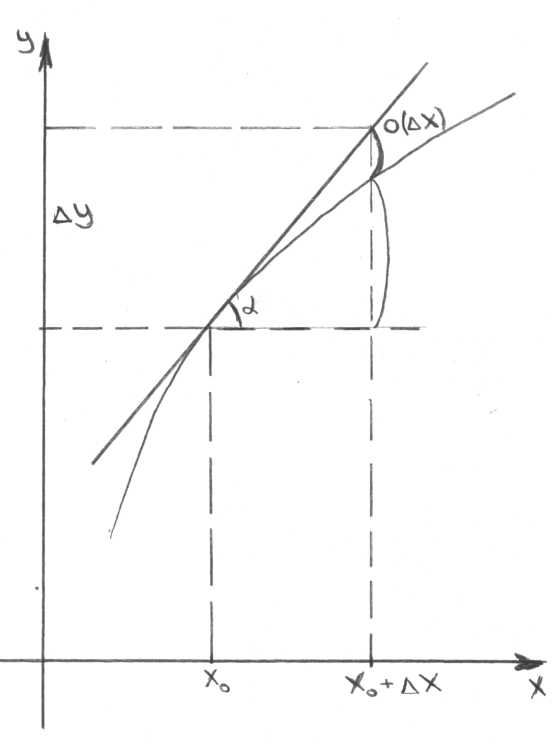
Таким образом, геометрический смысл дифференциала – это приращение ординаты касательной.

Лекция №10.

Связь между дифференцируемостью, наличием конечной производной и непрерывностью.

Если функция дифференцируема, то по определению дифференцируемости, она имеет конечную производную в точке , а значит, непрерывна в точке .

§5.5. Основные формулы и правила вычисления дифференциала.

Поскольку в случае дифференцируемости функции , то каждая формула вычисления производной дает формулу для вычисления дифференциала.

Пример:

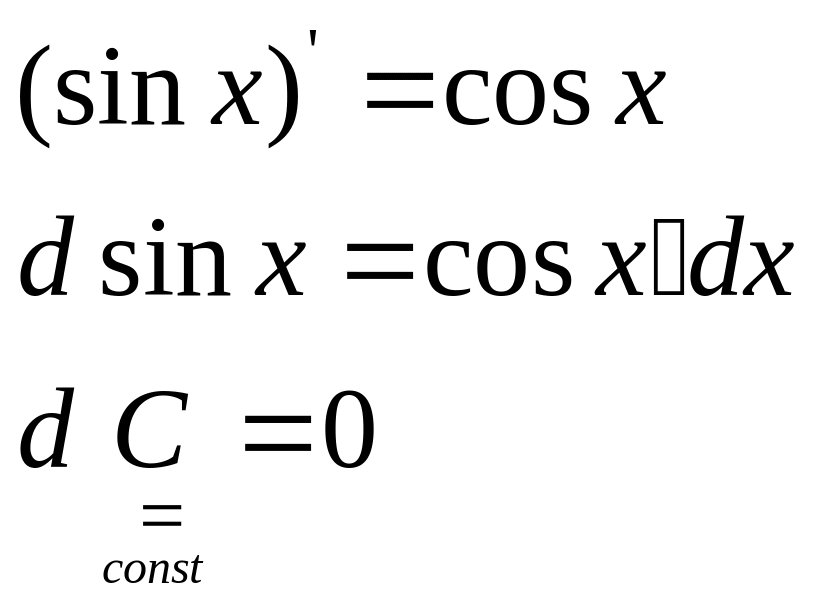
Теорема.

Если и дифференцируемы в точке , то:

1)

2)

3)

Дифференциал сложной функции. Инвариантность дифференциала сложной функции.

Теорема.

Пусть:

1)

и составим сложную функцию из функции

2) дифференцируема в точке , а дифференцируема в точке ,

Тогда (1)

Как видно из формулы формула для дифференциала сложной функции, где - промежуточная переменная, такая же как в случае, если бы была окончательной переменной.

Пример:

Это и называют инвариантностью формулы дифференциала. Формальной разницы между формулами нет, а фактическая есть.

- независимая переменная	- зависимая переменная
- приращение аргумента	- дифференциал некоторой функции, не совпадает просто с

Свойство инвариантности часто используют для вычисления.

§5.6. Использование дифференциала для приближенных вычислений.

Если функция дифференцируема, то ее полное приращение - б.м.ф. (бесконечно малая функция) при .