Теорема.
Для того, чтобы существовал
необходимо и достаточно, чтобы функция
,
где
- бмф при
.
Доказательство:
Утверждение, что
Пусть
т. к.
,
значит
- бмф при
Свойства бмф:
Свойство 1.
Сумма конечного числа бмф при снова есть бмф при .
и
- бмф при
.
Если
- бмф при
для
.
Таким образом
Свойство 2.
Произведение бмф при
на ограниченную функцию при
снова есть бмф при
.
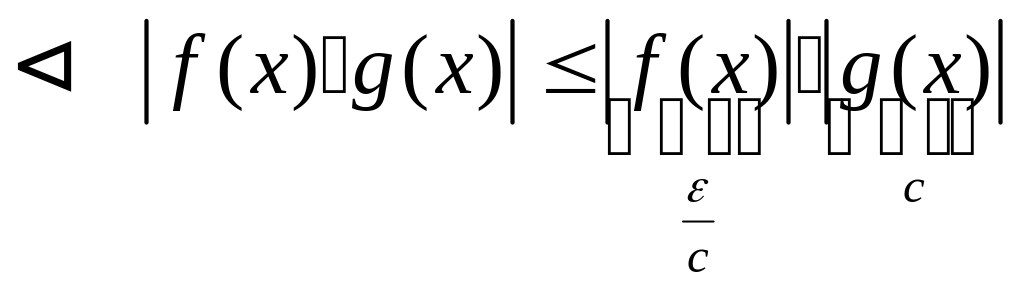
- ограниченная
Следствие 1.
Произведение бмф на постоянную функцию при есть бмф при .
Следствие 2.
Произведение конечного числа бмф при есть бмф при .
Пример:
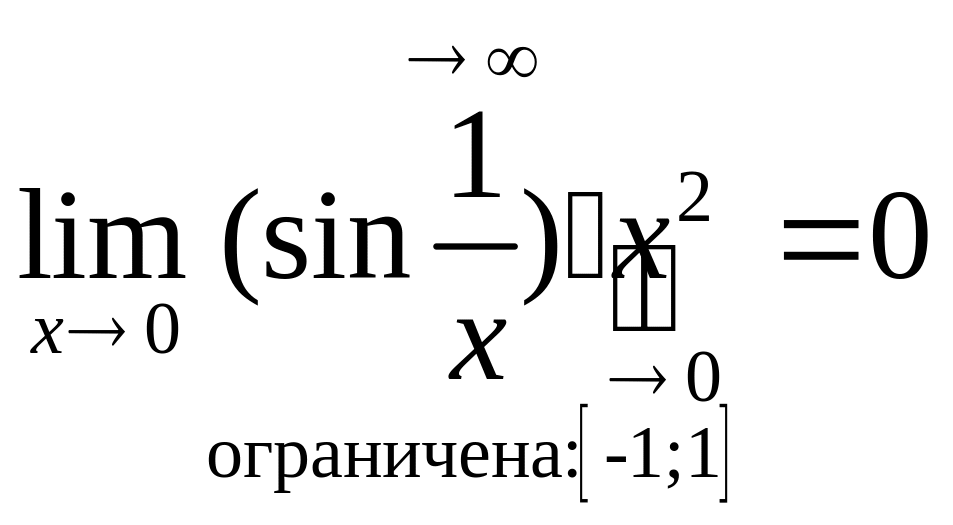
. Бесконечно большие функции (ббф).
Определение 3 Функция
называется ббф при
,
если
Свойства ббф:
Свойство 1: Сумма ббф при и ограниченной функции снова есть ббф.
Свойство 2 (связь между бмф и ббф):
а) Если
- бмф при
,
то
- ббф при
.
б) Если - ббф при , то - бмф при .
Лекция №5
§3.5. Пределы результатов арифметических действий. Теорема.
Пусть
и
конечный пределы функций, тогда:
1)
2)
3) при
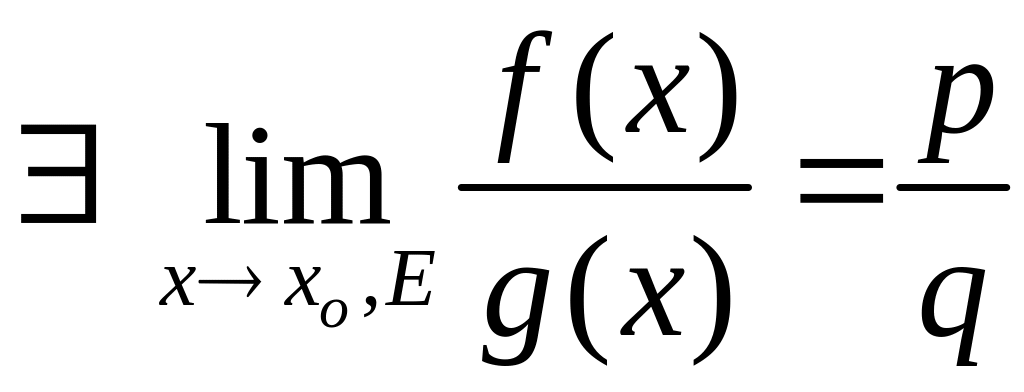
Следствие: Если существует
конечный предел функции
-
,
то для
.
Пример:
1)
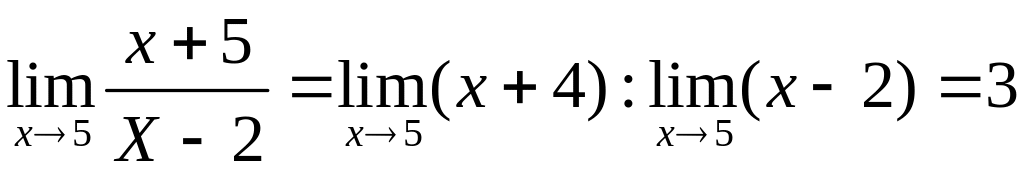
2)
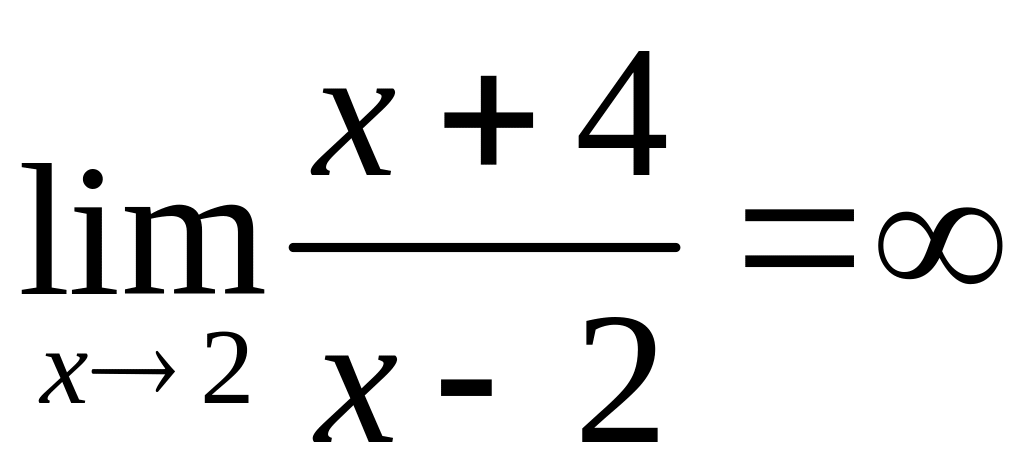
Если числитель и знаменатель одновременно стремятся к нулю, то дробь может иметь как конечный, так и бесконечный предел, а может и не иметь предел.
Когда
теорема не применима, т.к. выражение
не определено, но неверного результата
теорема не дает.
Пример:
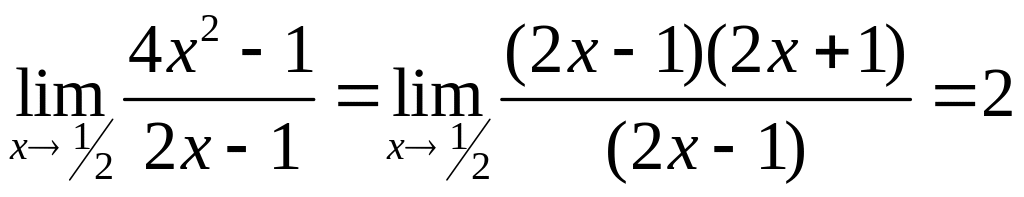
§3.6. Односторонние пределы.
Пусть
Введем обозначение :
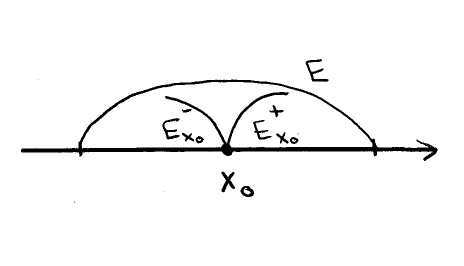
Определение. Односторонним
пределом
при
на
справа называется
.
Аналогично предел функции слева -
.
Пример:
Теорема(критерий существования двустороннего предела функции).
Для того, чтобы существовал предел
функции
(где
-
предельная для
и
)
необходимо и достаточно, чтобы существовали
и были равны между собой оба односторонних
предела.
§3.7. Свойство предела в области значений функции. Теорема 1.
Если существует предел функции
и
,
то существует окрестность точки
,такая
что
,
выполняется
.
Доказательство:
Т.к
,то
Возьмем
с левым концом
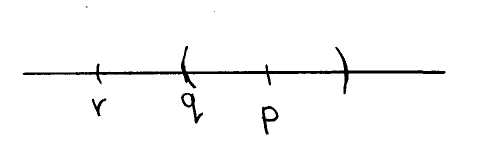
Поскольку
предел функции, то для выбранной
окрестности существует
,
так значение
Теорема 2.
Если:
1)
на
2)
и
тогда
Замечание. Из того, что
еще не следует, что
,
а можно лишь сказать, что
.
Пример:
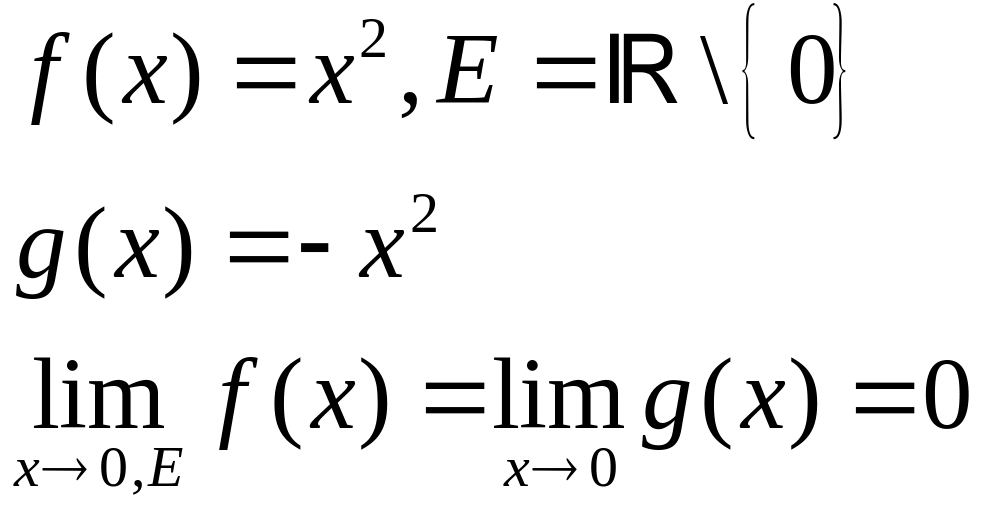
Теорема 3(принцип двух милиционеров).
Если:
1)
на
2)
и
Тогда
Доказательство:
Возьмем
,
т.к
является пределом функции
,
то для этой окрестности
т.к
является
,
то для выбранной окрестности
.
Для
,
попадающих в пересечение окрестностей
Пример:
Докажем первый замечательный предел:
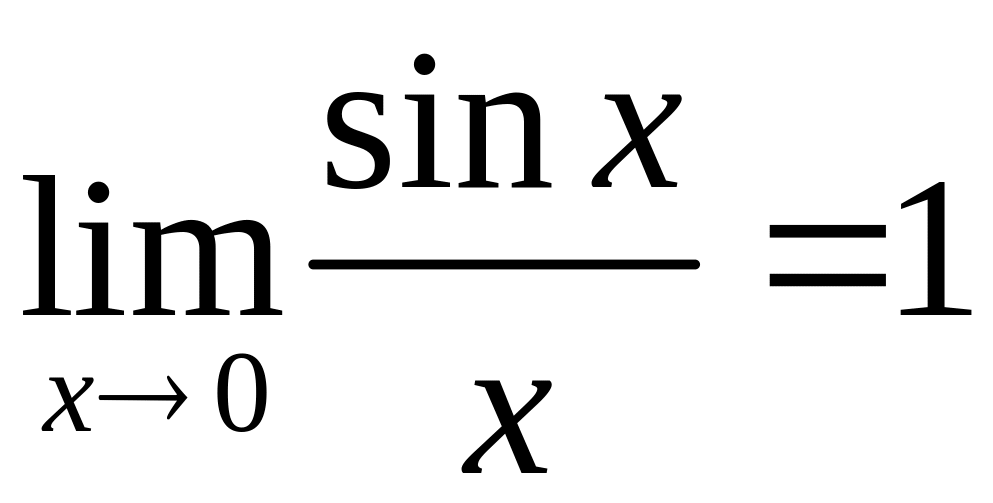
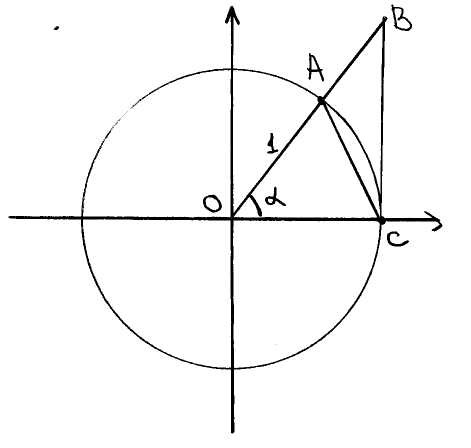
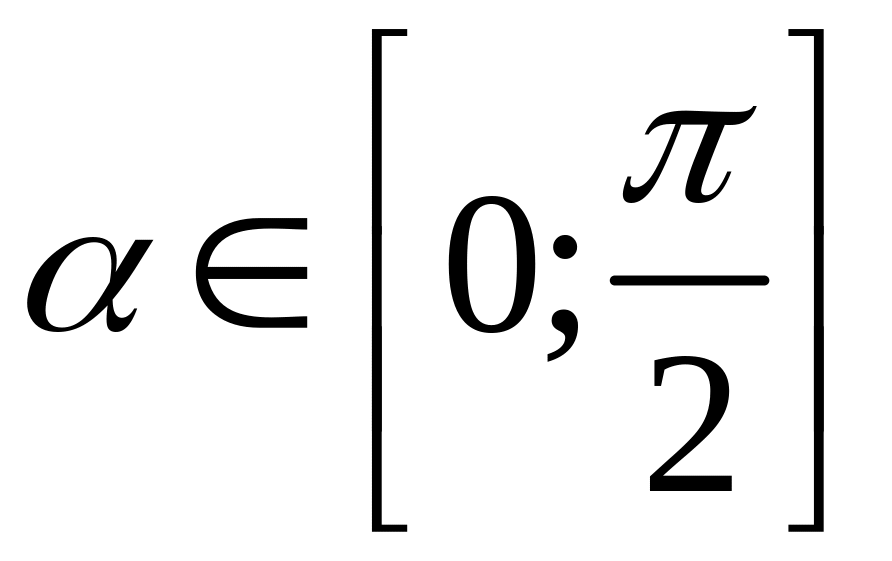
Как видно из рисунка:
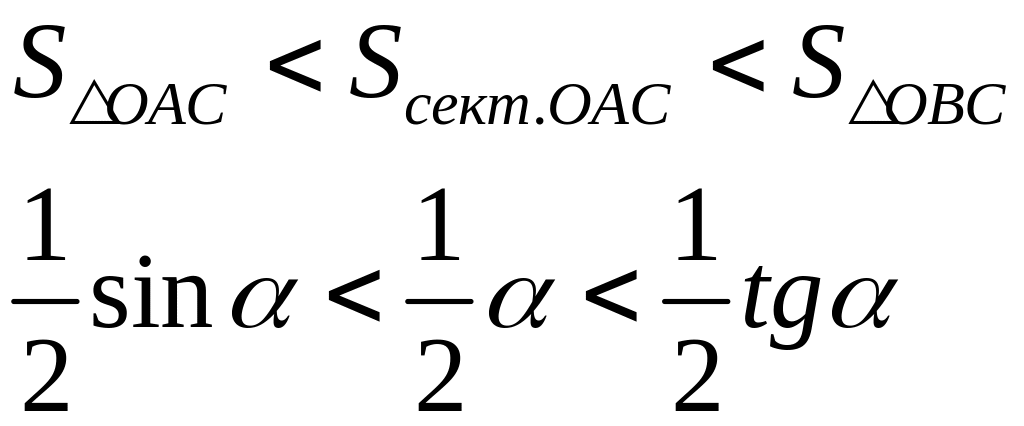
Поделим все на
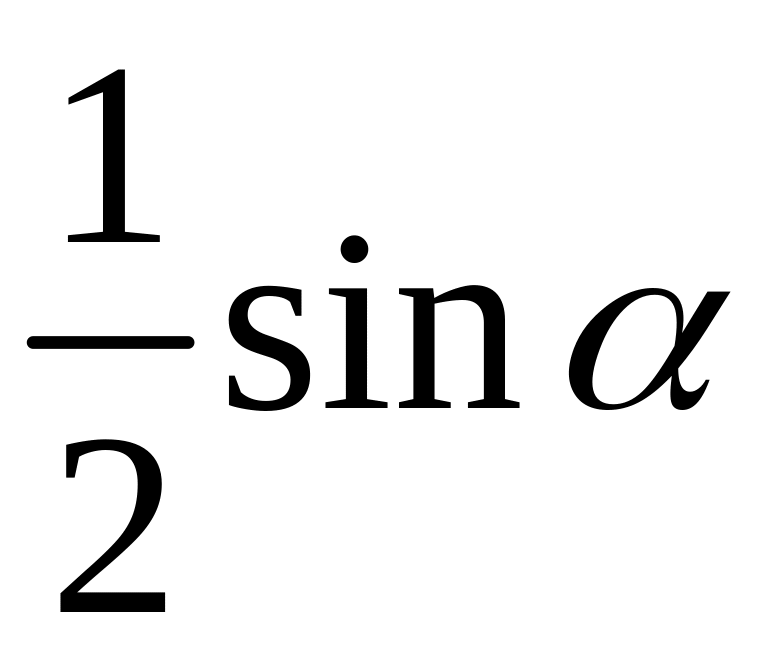
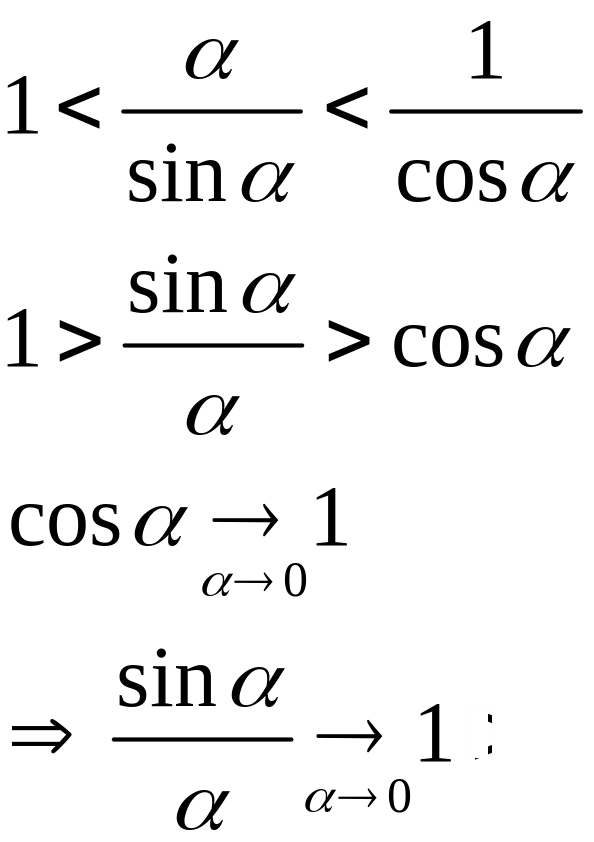
§3.8.Сравнение функции при на .
.Определение
1. Пусть заданы
и
.
Функция
называется б.м. по сравнению с функцией
при
на
(б.б по сравнению с функцией
при
на
),
если существует
функция
представима в виде:
,
где
В случае, если такое представление
возможно и
,
то говорят, что функция
эквивалентна функции
при
,
.
Если функция
на
,то
утверждение, что
-б.м.
по сравнению с
при
(что записывают так:
) равносильно утверждению, что
.
Пример:
Пусть
,
тогда
,
Замечание: В равенстве
правая часть не означает конкретную
функцию, а лишь означает, что речь идет
о функции б.м. при
,
поэтому из того, что
и
не следует, что
.
Свойство 1.
при
.
Свойство 2.
при
.
Свойство 3.
при
.
Доказательство свойства 3:
функция
представима в виде
,
где
-
б.м. на
,
тогда в этой же окрестности
.
.Определение
2. Функция
называется б.б. по сравнению с
,
если
при
.
Таким образом, например,
-б.б.
по сравнению
при
,
с другой стороны
-б.м.
по сравнению с
.
.Определение
3. Функция
называется ограниченной по сравнению
с
при
на
,
если
функция
представима в виде
,
где
-
ограниченная функция при
.
Обозначается :
при
.
Пример:
Требования определения 3 можно сформировать в другом виде:
при
.
Свойства:
Свойство 1. Если
,
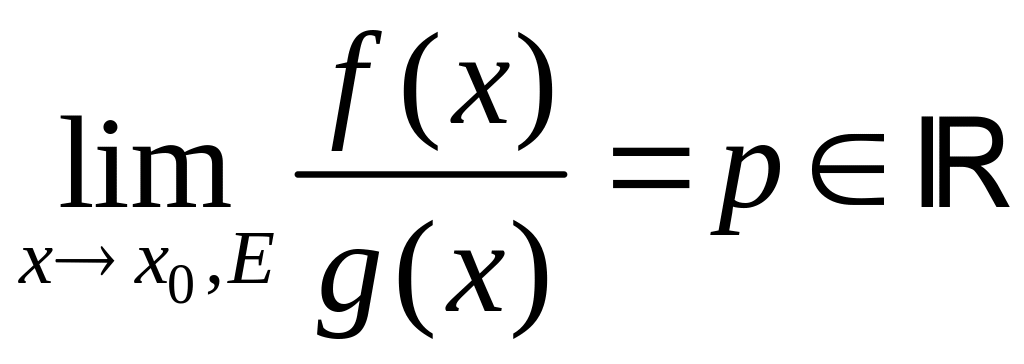то
при
Свойство 2.
Свойство 3.
Если одновременно выполняется, что
и
при
,
то говорят, что функции
и
одного порядка. Обозначение:
Пример:
при
и
функции одного порядка.
Лекция №6.
. Эквивалентные функции.
Определение Функции
и
называется эквивалентными при
,
если
.
Свойства эквивалентных функций:
Свойство 1.
Если
при
,
то:
а)
при
;
б) При условии, что
,
то
при
,
т.е. в произведении и частном операнды можно заменять эквивалентными выражениями.
Свойство 2.
Если
при
,
то
,
причем эти пределы оказываются равными
при условии их существования.
Пример:
что
при