10. Постулаты Бора...

Нильс Бор выдвинул следующие требования к атомной излучающей системе, которые впоследствии назвали постулатами Бора. (правила квантования)

1. Атомы могут определённое время, в зависимости от их структурных особенностей, находиться в определённых, так называемых стационарных состояниях. Энергии этих состояний E1,...,En образуют дискретный ряд. В стационарных состояниях атомы не излучают.

2. При переходе атома из одного состояния с энергией E2 в другое с энергией E1, происходит излучение, если E2>E1, или поглощение, если E2<E1 кванта света с частотой пропорциональной разности энергий состояний: ω=E2-E1/ђ

Б ор ввёл также правила, в соответствии с которыми определяются стационарные состояния атомных систем. Бор предположил, что стационарными являются лишь те состояния, в которых момент импульса электрона равен целому числу постоянных Планка: L=nђ. Коэффициент пропорциональности между моментом импульса электрона и постоянной Планка называют главным квантовым числом (так как оно определяет электронов, атома и его энергию). Р/м правила квантования на примере атома водорода. Электрон движется по круговой орбите с центростремительным ускорением, которое определяется силой кулоновского взаимодействия. По второму закону Ньютона мы можем записать: maн=Fk. Подставляя в это уравнение выражения для силы Кулона и центростремительного ускорения, получим (mvn2/rn)=(ze2/4πε0rn2), где n – главное квантовое число. Запишем правило квантования: mvnrn=nђ. Выразим из него скорость и подставим во второй закон Ньютона:

; ;

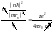. Мы нашли радиусы орбит основных состояний атома. В частности, радиус первой боровской орбиты составляет r1~=5*10-11м. Мы можем найти также энергию связи электрона в атоме – энергию, которую необходимо затратить, чтобы оторвать электрон от ядра. Полная энергия электрона в атоме равна сумме кинетической энергии его движения и потенциальной энергии его взаимодействия с ядром: Еполн=Екин+Епот. Подставляя значения этих энергий, получим: 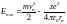. Подставим в эту формулу значение квадрата скорости, выраженное из второго закона Ньютона: . Подставим сюда значение боровского радиуса: , или . Таким образом, энергия связи определяется однозначно главным квантовым числом. Состояние атома с наименьшей энергией называется основным состоянием. Если атому каким-либо способом сообщается энергия, то атом переходит в другое энергетическое состояние. Состояние атома с энергией больше, чем энергия основного состояния называется возбуждённым. Так как основному состоянию атома соответствует главное квантовое число n=1, то первому возбуждённому состоянию –n=2.

Структура энергетических уровней атома водорода.

Из предыдущего следует, что атом обладает дискретным набором значений энергий, соответствующих различным энергетическим уровням. Вычисляя эти энергии, можно заметить, что с ростом главного квантового числа разность энергий между двумя соседними энергетическими состояниями всё время уменьшается. В конце концов, она будет стремиться к нулю.

Энергия, которую необходимо затратить, чтобы перевести атом из основного состояния в состояние с n=∞, называется энергией ионизации атома. Водорода потенциал ионизации составляет E=13,56эВ. Основываясь на представлении Бора о процессе излучения атома, можно сделать вывод, что спектральные серии соответствуют переходу атома с одних энергетических уровней на какой-то другой. Так, например, серии Лаймана соответствует переход атома водорода на первый энергетический уровень, серии Бальмера – на второй; серии Пашена – на третий. Этот факт позволяет найти длины волн в каждой серии. В соответствии со вторым постулатом Бора, мы можем записать, что при переходе с l – го энергетического уровня на n – й, излучается волна частоты . Как было сказано выше, Бальмер получил формулу для частоты излучённой волны: .Сравнивая её с предыдущей, получим:  . Мы получили формулу для определения постоянной Ридберга. Так как для атома водорода z=1, то постоянная Ридберга для атома водорода будет иметь вид: . Так как λ=2πc/ω, то . Отсюда постоянная Ридберга для длины волны будет: R’=1,09*10-5 см-1.

Различие между частотами, полученными по этой формуле, и при опыте всё равно присутствовало. Его объясняли так. При выводе формулы для радиусов боровских орбит, мы не учитывали тот факт, что электрон с ядром образуют систему двух тел, которая вращается вокруг общего центра масс. Данный факт можно учесть, если заменить в формуле для постоянной Ридберга массу электрона приведённой массой системы электрон – ядро: 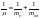, 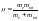. 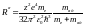, ; ; R''=Ř∞*1/(1+me/mяд). Найдём теперь спектральных линий между полученными экспериментально и теоретически: Δω=Ř*1-1//(1+me/mяд), , , . 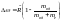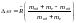Оцененная разность составила: Δω≈ω/4000, что совпадало с опытными данными.

Как следует из уравнения для постоянной Ридберга, для элементов с одинаковыми зарядами, но разной массой ядра, спектральные линии излучения должны отличаться. Такие элементы называют изотопами. Так как заряд ядра определяется количеством протонов, то изотопы различаются количеством нейтронов в ядре, а разница в частоте спектральных линий – изотопическим сдвигом. Для водорода существуют 3 изотопа: протий, дейтерий и тритий