9 . Опыты Резерфорда Ядерная модель атома.
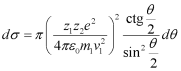
Модель
Резерфорда , приписывала атому строение,
аналогичное строению Солнечной системы:
в центре находится положительно
заряженное ядро, вокруг которого,
подобно планетам, движутся электроны,
удерживаемые у ядра силами кулоновского
притяжения.. Резерфорд изучал движение
тяжёлых положительно заряженных частиц
в поле, создаваемом атомом. Схема
использовавшейся установки приведена
на рисунке 31. Узкий пучок
– частиц из источника излучения падала
на тонкую золотую фольгу. За фольгой
находилась поверхность, покрытая
веществом, способным сцинтиллировать,
например,
.
– частицы пролетали сквозь фольгу и
падали на сцинтиллятор. Сцинтиллятор
на короткое время начинал светиться в
точке падения
– частиц. За этими вспышками как раз и
наблюдали. Если бы взаимодействия
частиц с веществом не было, то вспышки
наблюдались бы все в одном и том же
месте. Тем не менее, большинство частиц
отклонялись от направления своего
первоначального движения на 3°-5°, и что
ещё более интересно, приблизительно
одна из 6000 – 8000 частиц отклонялась от
первоначального направления движения
на угол более 90°. В то же время не было
частиц, которые притягивались бы - в
атоме должен находиться мощный силовой
центр, который заставляет отклоняться
частицы на большие углы, причём, так
как заряд
– частицы считался положительным, этот
силовой центр также должен быть
положительным. Редкость отскакивания
частицы на угол более 90° говорила о
том, что центр должен быть точечным. В
центре атома существует нечто, обладающее
большой массой и имеющее малые размеры
и положительный заряд. Изучая движение
частиц сквозь фольгу, Резерфорд получил
соотношение, связывающее угол рассеяния
частицы с прицельным параметром
.
Прицельным параметром
называется расстояние наименьшего
сближения частиц, при отсутствии
взаимодействия между ними (см. рис. 32)
(4).
П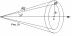
оследняя
формула была получена Резерфордом и
связывает угол рассеяния частицы с
прицельным параметром
.
Оставалось только проверить эту формулу.
В опыте Резерфорд имел дело не с одной
частицей, а с большим их числом. Частицы
двигались под некоторыми углами, то
есть имел место некоторый разброс
углов. Частицы рассеивались на различных
атомах и после рассеяния приобретали
некоторые импульсы, значения которых
также претерпевали некоторый разброс.
Для того чтобы описать данный процесс,
немыслимо пытаться рассчитывать
траекторию движения каждой частицы.
Полученная система уравнений будет
слишком громоздка и практически
неразрешима. В данном случае уместно
прибегнуть к теории вероятностей.
Введём понятие дифференциального
поперечного сечения рассеяния
в угол между
и
.
Так будем называть отношение числа
частиц dN
,
рассеянных в единицу времени в угол
к полному потоку частиц
:
.
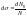Здесь
,
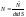где
– полное число частиц. Все частицы, для
которых
,
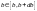будут рассеиваться в угол
.
Число частиц, прицельный параметр
которых заключён в этом интервале,
будет равно числу частиц, падающих на
кольцо шириной db и радиусом внутренней
окружности
:
.
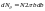Тогда
,.
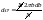Нам не важен здесь знак db, поэтому в
дальнейшем будем рассматривать лишь
его модуль. Воспользуемся теперь
полученной нами формулой (4) для нахождения
|db|: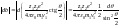
.
Подставляя
полученное выражение в уравнение для
,получим,
->
<
-
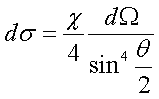Последняя формула называется формулой
Резерфорда. Перейдём теперь от плоского
угла
к телесному
.
Известно, что они связаны соотношением
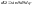в сферической системе координат. Тогда
если угол
,
.
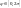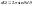Из последней формулы выразим
и подставим его в формулу Резерфорда
для плоского угла:
,
;
,
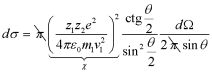или
<- (5). Мы получили формулу Резерфорда для телесного угла. Данная формула подтверждается с хорошей точностью и при современных исследованиях. Таким образом, косвенно подтвердилось уравнение (4), которое было выведено исходя
из соображений планетарного строения атома, что и утвердило главенствующее положение этой теории. Если известно сечение рассеяния , то с помощью формул (4) и (5) можно вычислить зарядовое число Z. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа.