
- •1. Фотоэффект.
- •2. Эффект Комптона.
- •3. Поляризация фотонов. Интерференция фотонов.
- •4. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •5 . Эффект Рамзауэра – Таунсенда.
- •6.Понятие волн де Бройля. Уравнения де Бройля. Эксперименты по волновой природе элементарных частиц
- •Эксперименты по волновой природе элементарных частиц.
- •7. Законы излучения абсолютно черного тела, формула Планка.
- •8. Опыт Франка-Герца. Атомные спектры.
- •9 . Опыты Резерфорда Ядерная модель атома.
- •10. Постулаты Бора...
- •11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.
- •13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
- •1 8.Прохождение частицы сквозь потенциальный барьер(туннельный эффект)
- •19. Контактная разность потенциалов, эффект холодной эмиссии электронов, альфа – распад.
- •20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
- •21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •22. Уравнение Шредингера для атомов щелочных метало, собственные значения и энергии.
- •23. Спектральные серии щелочных атомов, правила отбора
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •28.Эффект Пашена-Бака.
- •31.Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
- •32. Рентгеновские спектры.
27.Эффект Зеемана.
Как
известно, полный механический момент
атома
 .
Тогда проекция
.
Тогда проекция
 на какое-либо направление, в силу
пространственного квантования, будет
принимать
на какое-либо направление, в силу
пространственного квантования, будет
принимать
 значение. Так как проекция магнитного
момента связана с проекцией механического
момента через магнетон Бора, то и
проекция магнитного момента тоже может
принимать
значение. Так как проекция магнитного
момента связана с проекцией механического
момента через магнетон Бора, то и
проекция магнитного момента тоже может
принимать
 значение. Каждой ориентации магнитного
момента
значение. Каждой ориентации магнитного
момента
 будет соответствовать своя энергия
взаимодействия атома с магнитным полем:
будет соответствовать своя энергия
взаимодействия атома с магнитным полем:
 .
В этом случае
.
В этом случае
 .
Значит, возможны
энергии взаимодействия. Таким образом,
и полная энергия атома принимает
значение, то есть уровень энергии
расщепляется на
компоненту, а величина расщепления
определяется значениями проекции
магнитного момента или механического
момента. Для нахождения возможных линий
излучения необходимо учесть следующие
правила отбора для излучательных
переходов:
.
Значит, возможны
энергии взаимодействия. Таким образом,
и полная энергия атома принимает
значение, то есть уровень энергии
расщепляется на
компоненту, а величина расщепления
определяется значениями проекции
магнитного момента или механического
момента. Для нахождения возможных линий
излучения необходимо учесть следующие
правила отбора для излучательных
переходов:
 ;
;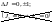 ;
; ;
;
Каждый
из возможных переходов приводит к
излучению отдельной линии. Явление
расщепления спектральных линий при
помещении атома в слабое внешнее
магнитное поле называют аномальным
(сложным) эффектом Зеемана. Полная
энергия равна, как было записано выше:
 .
Энергия излучения, при переходе с одного
уровня на другой, равна:
.
Энергия излучения, при переходе с одного
уровня на другой, равна:

 .
Таким образом, изменение частоты
.
Таким образом, изменение частоты
 будет равно:
будет равно:

 ,
,
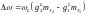 .
.
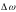 называют величину зеемановского
расщепления. Так как взаимодействие
магнитного момента с внешним магнитным
полем меньше, чем спин-орбитальное
взаимодействие, то и величина
зеемановского расщепления мала. Частота
излучения в случае слабого магнитного
поля определяется по формуле:
называют величину зеемановского
расщепления. Так как взаимодействие
магнитного момента с внешним магнитным
полем меньше, чем спин-орбитальное
взаимодействие, то и величина
зеемановского расщепления мала. Частота
излучения в случае слабого магнитного
поля определяется по формуле:
 .
.
Определим
величину смещения частоты при эффекте
Зеемана
 :
:
 .
.
Если
величина зеемановского расщепления
равна частоте ланморовой прецессии,
 ,
то такое расщепление называют нормальным
зеемановским расщеплением. Этот эффект
имеет место в том случае, когда
,
то такое расщепление называют нормальным
зеемановским расщеплением. Этот эффект
имеет место в том случае, когда
 .
Для первого уровня
.
Для первого уровня
 ,
а
,
а
 .
Таким образом, так как
.
Таким образом, так как
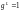 ,
а
,
а
 ,
то
,
то
 .
Следовательно, для синглетных уровней.
В слабом магнитном поле наблюдается
нормальное зеемановское расщепление:
.
Следовательно, для синглетных уровней.
В слабом магнитном поле наблюдается
нормальное зеемановское расщепление:
 .
.
Такой эффект называют простым (нормальным) эффектом Зеемана. Так как поле слабое, расщепление Зеемана будет меньше естественного (мультиплетного) расщепления, вызванного спин-орбитальным взаимодействием.
28.Эффект Пашена-Бака.
Рассмотрим
теперь случай, когда индукция магнитного
поля велика. В данной ситуации энергия
взаимодействия магнитного момента
атома с полем становится больше
спин-орбитального взаимодействия и
связь между спиновыми и орбитальными
моментами разрушается. Каждый в
отдельности начинает взаимодействовать
с полем. Это явление разрыва спин-орбитальной
связи в магнитном поле называется
эффектом Пашена – Бака. Энергия уровня,
в данном случае, равна:
 ,
где E0 – начальная энергия уровня до
помещения его в магнитное поле.
,
где E0 – начальная энергия уровня до
помещения его в магнитное поле.
 – запись через проекции
– запись через проекции на
на
 .
Тогда
.
Тогда
 .
Казалось бы, спектр должен быть очень
богатым, ведь возможны
.
Казалось бы, спектр должен быть очень
богатым, ведь возможны
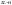 проекция
проекция
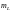 и
ещё две проекции
и
ещё две проекции .
Найдём его.
.
Найдём его.
 .
Для одного уровня
.
Для одного уровня
 ,
,
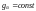 :
:
 ,
,
 .
.
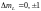 ;
;
 .
Тогда, если
.
Тогда, если
 и
и
 ,
,
 .
Следовательно,
.
Следовательно,
 .
Таким образом, может расщепляться на
три компоненты:
.
Таким образом, может расщепляться на
три компоненты: ;
;
 .
В эффекте Зеемана расщепление может
быть только для синглетных термов. В
эффекте Пашена – Бака любой терм
расщепляется на три.
.
В эффекте Зеемана расщепление может
быть только для синглетных термов. В
эффекте Пашена – Бака любой терм
расщепляется на три.
. 29. Эффект Штарка.
Явление Штарка состоит в том, что при наложении электрического поля энергетические уровни атомов, молекул и кристаллов расщепляются на подуровни и смещаются. Экспериментально это наблюдается в расщеплении и смещении спектральных линий в спектрах испускания и поглощения. Штарк подробно исследовал это явление на линиях серии Бальмера атома водорода. Позднее оно было обнаружено на молекулах и кристаллах.
Классическая теория не в состоянии объяснить эффект Штарка. Теория явления Штарка, основанная на полуклассической теории Бора, была построена Шварцшильдом и Эпштейном в 1916 г. Их основные результаты были подтверждены в квантово-механической теории Шредингера в 1926 г. В обеих теориях использовались методы теории возмущений, суть которой состоит в том, что при взаимодействии двух частиц учитывается основная энергия, то есть та энергия, которая максимальна. Далее решается уравнение Гамильтона. Потом учитываются малые поправки – малые энергии – возмущения.
Рассмотрим эффект
Штарка в атоме. Внешнее электрическое
поле будем считать однородным. Явление
Штарка проявляется по-разному в
зависимости от того, имеется ли у атома
в отсутствии внешнего электрического
поля собственный дипольный момент, или
нет. Если дипольный момент имеется, то
при наложении электрического поля
атом получает дополнительную энергию:
 ,
где
,
где
 – дипольный момент. Тогда смещение
энергетических уровней и расщепление
будут пропорциональны первой степени
напряжённости поля. Этот эффект и был
обнаружен Штарком. Если же у атома нет
собственного дипольного момента, то
при помещении атома во внешнее
электрическое поле, возбуждается
индуцированный дипольный момент. Этот
дипольный момент есть
– дипольный момент. Тогда смещение
энергетических уровней и расщепление
будут пропорциональны первой степени
напряжённости поля. Этот эффект и был
обнаружен Штарком. Если же у атома нет
собственного дипольного момента, то
при помещении атома во внешнее
электрическое поле, возбуждается
индуцированный дипольный момент. Этот
дипольный момент есть
 ,
где
,
где
 есть поляризуемость атома. При увеличении
электрического поля от 0 до
есть поляризуемость атома. При увеличении
электрического поля от 0 до
 ,
дипольный момент атома будет увеличиваться
от 0 до
,
дипольный момент атома будет увеличиваться
от 0 до
 ,
при этом над атомом будет совершаться
работа:
,
при этом над атомом будет совершаться
работа:
 .
Эта работа идёт на приращение энергии
атома в электрическом поле, а значит
на расщепление и смещение спектральных
линий (энергетических уровней). То есть
эффект Штарка в этом случае пропорционален
.
Эта работа идёт на приращение энергии
атома в электрическом поле, а значит
на расщепление и смещение спектральных
линий (энергетических уровней). То есть
эффект Штарка в этом случае пропорционален
 и называется квадратичным эффектом
Штарка. При прочих равных условиях
квадратичный эффект Штарка гораздо
меньше линейного эффекта Штарка.
и называется квадратичным эффектом
Штарка. При прочих равных условиях
квадратичный эффект Штарка гораздо
меньше линейного эффекта Штарка.
Если у атома был
дипольный момент, то возникает добавочный.
Его можно считать пропорциональным
полю. Тогда происходит наложение
квадратичного и линейного эффектов
Штарка. Картина расщепления становится
несимметричной, всё больше смещаясь в
сторону низких энергий, и тем сильнее,
чем выше они расположены. Спектральные
линии смещаются в сторону меньших
частот. Это смещение не велико. Для
серии Бальмера
 .
Расстояние между крайними:
.
Расстояние между крайними:
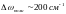 .
.
Если напряжённость
поля меньше
 ,
квадратичный эффект Штарка практически
не сказывается. Его необходимо учитывать
при напряжённостях порядка
,
квадратичный эффект Штарка практически
не сказывается. Его необходимо учитывать
при напряжённостях порядка
 .
.
