
- •1. Фотоэффект.
- •2. Эффект Комптона.
- •3. Поляризация фотонов. Интерференция фотонов.
- •4. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •5 . Эффект Рамзауэра – Таунсенда.
- •6.Понятие волн де Бройля. Уравнения де Бройля. Эксперименты по волновой природе элементарных частиц
- •Эксперименты по волновой природе элементарных частиц.
- •7. Законы излучения абсолютно черного тела, формула Планка.
- •8. Опыт Франка-Герца. Атомные спектры.
- •9 . Опыты Резерфорда Ядерная модель атома.
- •10. Постулаты Бора...
- •11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.
- •13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
- •1 8.Прохождение частицы сквозь потенциальный барьер(туннельный эффект)
- •19. Контактная разность потенциалов, эффект холодной эмиссии электронов, альфа – распад.
- •20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
- •21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •22. Уравнение Шредингера для атомов щелочных метало, собственные значения и энергии.
- •23. Спектральные серии щелочных атомов, правила отбора
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •28.Эффект Пашена-Бака.
- •31.Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
- •32. Рентгеновские спектры.
26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
П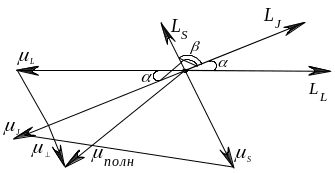 олный
маг момент атома складывается из полных
спинового и орбитального моментов
атома:
олный
маг момент атома складывается из полных
спинового и орбитального моментов
атома:
 .
Для каждого из них мы можем записать:
.
Для каждого из них мы можем записать: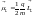 и
и
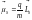 .
Таким образом, полный механический
момент не будет лежать на одной оси с
полным механическим моментом.
.
Таким образом, полный механический
момент не будет лежать на одной оси с
полным механическим моментом.
Рассмотри
случай изолированного атома. В
изолированном атоме Lj=const. Если вектор
Lj сохраняет своё направление в
пространстве, вектора
 и
и
 должны
прецессировать вокруг
должны
прецессировать вокруг
 .
Прецессируют и полные механический
и магнитный моменты.
.
Прецессируют и полные механический
и магнитный моменты.
Найдём
связь между
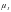 и
и
 .
Из рисунка видно, что
.
Из рисунка видно, что
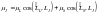 (1).
(1).
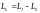 (2),
(2),
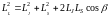 .
Следовательно,
.
Следовательно,
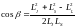 .
Найдём cos(α). Из уравнения (2) следует,
что
.
Найдём cos(α). Из уравнения (2) следует,
что
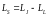 ,
,
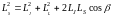 ;
;
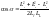 .
Запишем уравнения для проекции
магнитного момента на направление
вектора
.
Запишем уравнения для проекции
магнитного момента на направление
вектора
 :
:
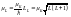 :
: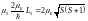 Подставим
последние два выражения в (1) с учётом
полученных выше выражений для косинусов:
Подставим
последние два выражения в (1) с учётом
полученных выше выражений для косинусов:
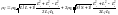
Подставим значения
для каждого момента, выраженное через
квантовые числа:

Выражение ,
помещённое в круглых скобках, называется
фактором Ланде:
 .
Таким образом,
.
Таким образом,
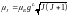 (3). Выражение (3) аналогично тому,
которое связывает спиновой орбитальный
момент с орбитальным механическим. Из
этой аналогии следует смысл фактора
Ланде – это гиромагнитное отношение
для полного магнитного момента.
(3). Выражение (3) аналогично тому,
которое связывает спиновой орбитальный
момент с орбитальным механическим. Из
этой аналогии следует смысл фактора
Ланде – это гиромагнитное отношение
для полного магнитного момента.
L-S связь. Реализуется в том случае, если электростатическое взаимодействие между электронами в атоме сильнее, чем спин-орбитальное взаимодействие для каждого электрона. Поэтому сначала находятся полный орбитальный и полный спиновой моменты для каждого электрона, которые потом складываются:
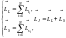 .Полный
момент, очевидно, квантуется:
.Полный
момент, очевидно, квантуется:
 ,
где
,
где
 .
Как было показано выше, число способов,
которыми складываются моменты, равно
числу слагаемых:
.
Как было показано выше, число способов,
которыми складываются моменты, равно
числу слагаемых:
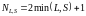 ,
то есть возможно
,
то есть возможно
 состояний атома. Обычно бывает S < L.
Тогда
состояний атома. Обычно бывает S < L.
Тогда
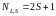 .
.
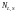 определяет спин-орбитальное расщепление
энергетических уровней в атоме и
называется мультиплетностью.
определяет спин-орбитальное расщепление
энергетических уровней в атоме и
называется мультиплетностью.
2.
J-J связь Этот тип связи реализуется,
когда спин-орбитальное взаимодействие
в атоме сильнее, чем электростатическое
взаимодействие различный электронов
друг с другом. Поэтому мы находим сначала
полный механический момент всех
электронов, а потом – полный момент
всего атома как векторную сумму всех
полных моментов каждого электрона:
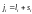 ,
,
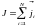 .
Этот тип связи реализуется для
многоэлектронных атомов (окончание
таблицы Менделеева).
.
Этот тип связи реализуется для
многоэлектронных атомов (окончание
таблицы Менделеева).
Отношение μ/L модуля магнитного момента к модулю механического момента, выраженное в единицах e/2m, называется гиромагнитным отношением: μ/L= e/2m =g. Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е. gl=1. Для собственного магнитного момента электрона, обусловленного наличием спина: μ s= eLs/m. Тогда гиромагнитное отношение для спинового магнитного момента и механического момента gs=2.
