24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.

Каждый рентгеновский терм соответствует состоянию оболочки, из которой удален один из эл-нов. У замкнутой оболочки полный орбитальный момент , полный спиновый , и полный механический омент равны 0. Если из этой оболочки удален эл-н с некоторыми моментами , , , то оставшаяся конфигурация будет обладать полными моментами, численно равными моментам удаленного эл-на. Энергетические состояния замкнутой оболочки без одного эл-на имеют такую же мультиплетность, как и энергетические состояния одного эл-на. Т.к. термы одного эл-на дублетны, то и рентгеновские термы должны быть дублетными.

Спин - собственный момент количества движения электрона, имеющий квантовую природу и не связанный с перемещением частицы как целого. С. измеряется в единицах постоянной Планка ħ и равен Jh, J — характерное для каждого целое (в т. ч. нулевое) или дробное положительное число, называемое спиновым квантовым числом. С. электрона равен 1/2, С. Проекция С. на любое фиксированное направление z в пространстве может принимать значения J, J—1, ..., —J. Т. о., частица со С. J может находиться в 2J + 1 спиновых состояниях (при J = 1/2 — в двух состояниях), что эквивалентно наличию у неё дополнительной внутренней степени свободы. Квадрат вектора С., согласно квантовой механике, равен Магнитомеханическое отношение существует у электрона собственный механический

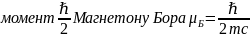
е и m — заряд и масса электрона, с — скорость света). Т. о., для С. электрона отношение магнитного момента к механическому равно γ = е/mс и с точки зрения классической электродинамики является аномальным: для орбитального движения электрона и для любого движения классической системы заряженных частиц с данным отношением е/m оно в 2 раза меньше и равно е/2mс.

25. Маг и мех моменты электрона. Правило квантования.

Итак, электрон обладает в атоме четырьмя моментами:

1. Механическим (орбитальным и спиновым);

2. Магнитным (орбитальным и спиновым).

П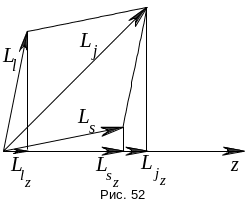 олный механический момент импульса электрона является векторной суммой орбитального механического момента и спинового механического момента: . Так как модули каждого момента всегда квантуются: , то и их сумма должна квантоваться: , где – квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось Z: – значение; . Тогда ; , где 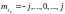– 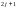значение. Так как , то тогда . Определим угол между орбитальным и спиновым моментами электрона. Так как , то, возводя это выражение в квадрат, получим: . Отсюда , или . Так как возможно лишь – 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).

Полный магнитный момент электрона равен сумме векторов орбитального магнитного момента и спинового магнитного момента: . Так как . Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.