
- •1. Фотоэффект.
- •2. Эффект Комптона.
- •3. Поляризация фотонов. Интерференция фотонов.
- •4. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •5 . Эффект Рамзауэра – Таунсенда.
- •6.Понятие волн де Бройля. Уравнения де Бройля. Эксперименты по волновой природе элементарных частиц
- •Эксперименты по волновой природе элементарных частиц.
- •7. Законы излучения абсолютно черного тела, формула Планка.
- •8. Опыт Франка-Герца. Атомные спектры.
- •9 . Опыты Резерфорда Ядерная модель атома.
- •10. Постулаты Бора...
- •11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.
- •13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
- •1 8.Прохождение частицы сквозь потенциальный барьер(туннельный эффект)
- •19. Контактная разность потенциалов, эффект холодной эмиссии электронов, альфа – распад.
- •20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
- •21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •22. Уравнение Шредингера для атомов щелочных метало, собственные значения и энергии.
- •23. Спектральные серии щелочных атомов, правила отбора
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •28.Эффект Пашена-Бака.
- •31.Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
- •32. Рентгеновские спектры.
20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
Р/м
движение эл-на в центрально-симметричном
кулоновском поле ядра. Ур-е Шр-ра для
частицы в центрально-симметричном
поле:
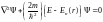 .
Будем р/м движение частицы в сферической
системе координат.
.
Будем р/м движение частицы в сферической
системе координат.
 (1), где
(1), где
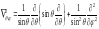 (1). Решение уравнения Шредингера будем
искать в виде:
(1). Решение уравнения Шредингера будем
искать в виде:
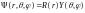 .
Подст-я реш в ур Шредингера:
.
Подст-я реш в ур Шредингера:
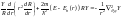
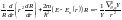 .
Так как обе части этого уравнения входят
независимые переменные и эти части
равны, то мы должны положить
.
Так как обе части этого уравнения входят
независимые переменные и эти части
равны, то мы должны положить
 .
Т.о, это ур распадается на 2:
.
Т.о, это ур распадается на 2:
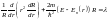 (2) и
(2) и
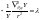 (3). Рассмотрим сначала решение ур
(3). Распишем лапласиан, связанный с
поворотом тела в прост-ве:
(3). Рассмотрим сначала решение ур
(3). Распишем лапласиан, связанный с
поворотом тела в прост-ве:
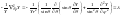 .
.
 .
Так как
.
Так как
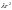 не зависит ни от
,
ни от
не зависит ни от
,
ни от
 ,
то
,
то
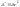 =const
Тогда
=const
Тогда
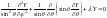 .
Будем искать его решение в виде:
.
Будем искать его решение в виде:

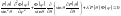 Разделим
на
Разделим
на
 :
:
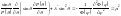 ,
где
,
где
 – константа разделения. Разобьём это
ур на 2 части:
– константа разделения. Разобьём это
ур на 2 части:
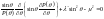 и
и
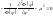 ,
,
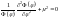 .
Запишем систему
.
Запишем систему
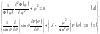
Решение
первого уравнения данной системы имеет
вид:
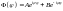 .
Из требования однозначности решения
следует, что
.
Из требования однозначности решения
следует, что
 должно быть любым положительным или
отрицательным числом. Поэтому все
собственные функции дифференциального
уравнения (4) могут быть представлены
формулой:
должно быть любым положительным или
отрицательным числом. Поэтому все
собственные функции дифференциального
уравнения (4) могут быть представлены
формулой:
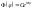 ,
где m=0,+-1,+-2. Постоянная C находится из
условия нормировки и равна
,
где m=0,+-1,+-2. Постоянная C находится из
условия нормировки и равна
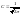 .
Т.образом,
.
Т.образом,
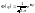 .
Решая уравнение (5), перейдём к новым
координатам:
.
Решая уравнение (5), перейдём к новым
координатам:
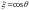 .
Тогда
.
Тогда
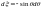 и
и
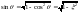 ;
dθ=-dξ/√(1-ξ2). С учётом последних
преобразований перепишем уравнение
(5):
;
dθ=-dξ/√(1-ξ2). С учётом последних
преобразований перепишем уравнение
(5):
 .
Чтобы привести данное уравнение к
стандартному виду введём обозначение:
.
Чтобы привести данное уравнение к
стандартному виду введём обозначение:
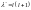 ,
где l – неотрицательное целое число.
Тогда решением данного уравнения будет
присоединённый полином Лежандра:
,
где l – неотрицательное целое число.
Тогда решением данного уравнения будет
присоединённый полином Лежандра:
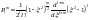 .
Причём, при заданном l, m может принимать
только 2l+1 значение:
.
Причём, при заданном l, m может принимать
только 2l+1 значение:
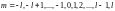 .
Волновая функция должна удовлетворять
условию нормировки:
.
Волновая функция должна удовлетворять
условию нормировки:
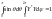 ;
;
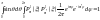 .
Так как
.
Так как
 и
связаны однозначно, то мы можем переписать
последний интеграл в виде:
и
связаны однозначно, то мы можем переписать
последний интеграл в виде:
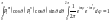 .
Выражение, стоящее под внутренним
интегралом, не зависит от
,
поэтому мы можем вычислять каждый
интеграл по отдельности и полученные
значения перемножить. Известно, что
.
Выражение, стоящее под внутренним
интегралом, не зависит от
,
поэтому мы можем вычислять каждый
интеграл по отдельности и полученные
значения перемножить. Известно, что
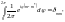 ,
где
,
где
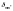 – символ Кронекера. Второй интеграл
даёт значение
– символ Кронекера. Второй интеграл
даёт значение
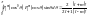 .
Собственная функция уравнения (5)
запишется в виде:
.
Собственная функция уравнения (5)
запишется в виде:
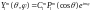 .
Тогда с помощью условия нормировки, мы
можем записать:
.
Тогда с помощью условия нормировки, мы
можем записать:
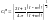 .
.
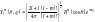 .
Мы получили угловую функцию, описывающую
движение частиц в центрально –
симметричном поле.
.
Мы получили угловую функцию, описывающую
движение частиц в центрально –
симметричном поле.
21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
Рассмотрим
потенциальную энергию частицы:
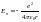 .
Решим уравн Шредингера для потенциальной
составляющей:
.
Решим уравн Шредингера для потенциальной
составляющей:
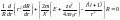 .
Введём следующие обозначения:
.
Введём следующие обозначения: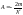 ;
;
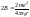 .
Замена переменных:
.
Замена переменных: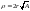 ,
,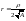 ;
;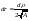 .
Тогда уравнение примет вид:
.
Тогда уравнение примет вид:
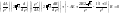
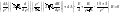
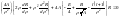
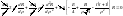
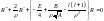 (1).
(1).
1)Р/м
сначала асимптотическое решение при
p→∞. Тогда(1) преобр к виду:
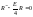 .
Решением его будет
.
Решением его будет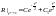 .
Чтобы решен было ограничено на
бесконечности, необходимо положить
.
Чтобы решен было ограничено на
бесконечности, необходимо положить
 ;
;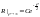 .
.
2)Теперь
рассмотрим ассимптотику при p→0: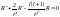 .
Решение будем искать ввиде:
.
Решение будем искать ввиде: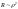 :
: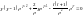 ,
,
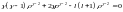 ,
,
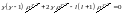 ;
;
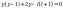 .
Мы получили уравнение относительно
.
Мы получили уравнение относительно :
: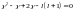 ,
,
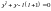 .
.
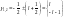 .
Если
.
Если
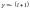 ,
то
,
то
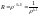 .
При p→∞, p→0. Поэтому данное
.
При p→∞, p→0. Поэтому данное
 придётся отбросить. Т.о, остаётся
решение:
придётся отбросить. Т.о, остаётся
решение:
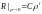 .
.
Решение
для радиальной составляющей волновой
функции мы будем искать в виде:
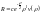 .
Здесь ν(p) – некот функция, которая
определяет поведение R в промежутке от
0 до бескон. Подставляем данный вид
реш-я в (1):
.
Здесь ν(p) – некот функция, которая
определяет поведение R в промежутке от
0 до бескон. Подставляем данный вид
реш-я в (1):
 (2). Введём ограничен на функцию
(2). Введём ограничен на функцию
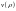 :
она не должна на бескон расти быстрее,
чем
:
она не должна на бескон расти быстрее,
чем
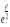 ,
а в 0 должна либо обращаться в 0, либо
быть const,
,
а в 0 должна либо обращаться в 0, либо
быть const,![]() .
Подставим в (2):
.
Подставим в (2):
![]()

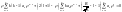
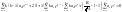
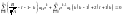 .
.
Данный
многочлен будет равен нулю только в
том случае, когда коэффициенты при
каждой степени p будут равны нулю:
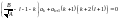 .
Данное соотношение даёт рекуррентную
формулу
.
Данное соотношение даёт рекуррентную
формулу
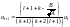 .
Оценим коэффициенты ak при k→∞:
.
Оценим коэффициенты ak при k→∞:
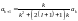 ,
,
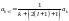
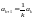 .
Т.о,
.
Т.о,
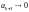 и
и
 .
Тогда при каком-нибудь малом значении
.
Тогда при каком-нибудь малом значении
 многочлен можно оборвать:
многочлен можно оборвать:
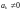 ,
а
,
а
 .
Данное услов будет выполнено, если
коэффициент при
.
Данное услов будет выполнено, если
коэффициент при
 будет равен нулю:
будет равен нулю:
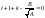 ,
,
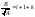 ;.
;.
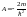 ,
,
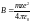 .
.
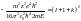 .
.
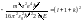 ,
,
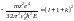 .
Из этой формулы следует, что энергия
зависит от l и k. Введём следующее
обозначение: l+k+1=n. Тогда
, где n=1,2,... Таким образом, решая уравнение
Шредингера, мы нашли энергии
водородоподобного атома, то есть нашли
собственные значения оператора
Гамильтона.
.
Из этой формулы следует, что энергия
зависит от l и k. Введём следующее
обозначение: l+k+1=n. Тогда
, где n=1,2,... Таким образом, решая уравнение
Шредингера, мы нашли энергии
водородоподобного атома, то есть нашли
собственные значения оператора
Гамильтона.
