- •1. Фотоэффект.
- •2. Эффект Комптона.
- •3. Поляризация фотонов. Интерференция фотонов.
- •4. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •5 . Эффект Рамзауэра – Таунсенда.
- •6.Понятие волн де Бройля. Уравнения де Бройля. Эксперименты по волновой природе элементарных частиц
- •Эксперименты по волновой природе элементарных частиц.
- •7. Законы излучения абсолютно черного тела, формула Планка.
- •8. Опыт Франка-Герца. Атомные спектры.
- •9 . Опыты Резерфорда Ядерная модель атома.
- •10. Постулаты Бора...
- •11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.
- •13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
- •1 8.Прохождение частицы сквозь потенциальный барьер(туннельный эффект)
- •19. Контактная разность потенциалов, эффект холодной эмиссии электронов, альфа – распад.
- •20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
- •21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •22. Уравнение Шредингера для атомов щелочных метало, собственные значения и энергии.
- •23. Спектральные серии щелочных атомов, правила отбора
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •28.Эффект Пашена-Бака.
- •31.Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
- •32. Рентгеновские спектры.
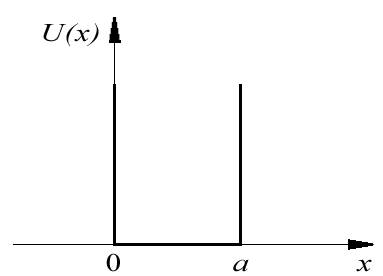
16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия
частицы ![]() имеет
вид
имеет
вид
![]()
![]()
т.е.
внутри ямы (![]() )
потенциальная энергия
)
потенциальная энергия ![]() постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
|
Уравнение Шредингера и его решение для частицы в одномерной потенциальной яме с бесконечно высокими стенками^
Уравнение
Шредингера:
![]() ,
где ψ – волновая функция, Е – энергия
частицы.
,
где ψ – волновая функция, Е – энергия
частицы.
Для
случая U
= 0, получим
![]() или
или
![]() ,
где a2
= 2mE/
,
где a2
= 2mE/![]() 2.
Это уравнение описывает положение
частицы внутри потенциальной ямы. Оно
имеет решение, представляющее собой
суперпозицию двух волн, распространяющихся
в противоположных направления вдоль
оси x.
2.
Это уравнение описывает положение
частицы внутри потенциальной ямы. Оно
имеет решение, представляющее собой
суперпозицию двух волн, распространяющихся
в противоположных направления вдоль
оси x.
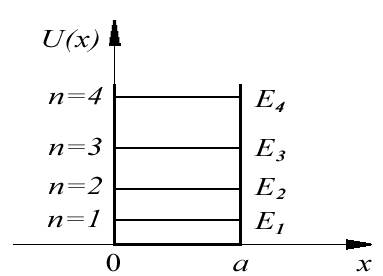
Итак, соотношение для энергии частицы в бесконечной прямоугольной яме:
|
(4.16) |
Важной особенностью полученного энергетического спектра (4.16) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (4.16). Отметим, что решение
|
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.
Число ![]() в (4.16) ,
определяющее энергию частицы в яме,
называется квантовым
числом,
а соответствующее ему значение
в (4.16) ,
определяющее энергию частицы в яме,
называется квантовым
числом,
а соответствующее ему значение ![]() -
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с
-
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с ![]() ,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение
,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение ![]() отвечает
первому возбужденному состоянию,
значение
отвечает
первому возбужденному состоянию,
значение ![]() -
второму возбужденному состоянию и т.д.
-
второму возбужденному состоянию и т.д.
Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики. В классической механике минимальную энергию, равную нулю, имеет покоящаяся в яме частица. Такого состояния покоя у квантовой частицы не существует.
17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
Рассмотрим случай несимметричной ямы: один барьер бесконечный, а другой имеет конечные размеры. Рассмотрим движение в двух областях: 0<x<a и x>a.
В первой области уравнение Шредингера имеет вид
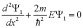 .
Вводя обозначение
.
Вводя обозначение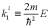 ,
получим:
,
получим: .
Решение этого уравнения аналогично
предыдущему пункту:
.
Решение этого уравнения аналогично
предыдущему пункту: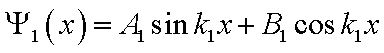 .
Из граничных условий, которые
соответствуют (1), получаем, что B1=0 и
.
Из граничных условий, которые
соответствуют (1), получаем, что B1=0 и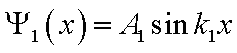 .
.Во второй области уравнение Шредингера имеет вид:
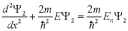 или
или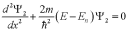 .
Введём здесь обозначение:
.
Введём здесь обозначение: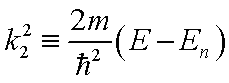 С
учётом обозначения можно записать:
С
учётом обозначения можно записать: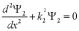 .
Решение данного уравнения зависит от
k2. Имеют место два случая:
.
Решение данного уравнения зависит от
k2. Имеют место два случая:
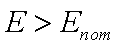 и
и
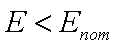 в зависимости от знака k. Разберём
каждый случай.
в зависимости от знака k. Разберём
каждый случай.
1.Случай
Общий
вид решения исходного уравнения задаётся
формулой:![]() .
Волновая функция частоты должна быть
непрерывна. Этот факт математически
выражается так:
.
Волновая функция частоты должна быть
непрерывна. Этот факт математически
выражается так:
![]() и
и
![]() (2). Подставляя значения функций,
получим:
(2). Подставляя значения функций,
получим:
![]() или
или
![]() .
Считая производные и удовлетворяя
равенству (2), получим:
.
Считая производные и удовлетворяя
равенству (2), получим:![]() или
или![]() .
Мы получили систему уравнений:
.
Мы получили систему уравнений:![]() .
Эти условия всегда могут быть
удовлетворены. Поэтому в случае
спектр энергии непрерывен, частица при
своём движении не локализована в
конечной области пространства, её
движение инфинитно.
.
Эти условия всегда могут быть
удовлетворены. Поэтому в случае
спектр энергии непрерывен, частица при
своём движении не локализована в
конечной области пространства, её
движение инфинитно.
Случай . В этом случае
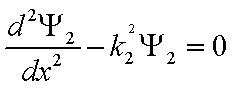 .
Решением этого уравнения будет функция
следующего вида:
.
Решением этого уравнения будет функция
следующего вида: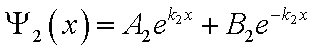 .
Первое слагаемое в данном уравнении
не имеет физического смысла, иначе
волновая функция неограниченно
возрастать с увеличением x. Поэтому мы
обязаны положить A2=0. Получится
уравнение:
.
Первое слагаемое в данном уравнении
не имеет физического смысла, иначе
волновая функция неограниченно
возрастать с увеличением x. Поэтому мы
обязаны положить A2=0. Получится
уравнение: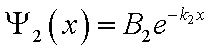 .
Эта функция ограничена для любого
значения
энергии. Однако даже если энергия
частицы меньше энергии потенциального
барьера, то всё равно существует
вероятность обнаружить частицу за
барьером. С ростом x волновая функция
убывает.
.
Эта функция ограничена для любого
значения
энергии. Однако даже если энергия
частицы меньше энергии потенциального
барьера, то всё равно существует
вероятность обнаружить частицу за
барьером. С ростом x волновая функция
убывает.
П опробуем
теперь найти возможные значения энергии,
которые будут принимать частица в том
случае, если её энергия будет меньше
энергии потенциального барьера:
.
Рассмотрим уравнения волновых функций
в двух различных областях:
опробуем
теперь найти возможные значения энергии,
которые будут принимать частица в том
случае, если её энергия будет меньше
энергии потенциального барьера:
.
Рассмотрим уравнения волновых функций
в двух различных областях:![]() ,
.
Из соображений конечности волновой
функции и её непрерывности мы можем
записать:
и
.
Подставляя конкретный вид соответствующей
функции, получим:
,
.
Из соображений конечности волновой
функции и её непрерывности мы можем
записать:
и
.
Подставляя конкретный вид соответствующей
функции, получим:
![]() и
и![]() .
Разделим второе уравнение на первое.
В результате получим:
.
Разделим второе уравнение на первое.
В результате получим:![]() ,
,![]() (3). Найдём возможные значения k1 и k2,
чтобы найти возможные значения энергии.
Известно, что
(3). Найдём возможные значения k1 и k2,
чтобы найти возможные значения энергии.
Известно, что![]() ,
а
,
а![]() .
Возвращаясь к выражениям (3) и используя
только что приведённые, получим:
.
Возвращаясь к выражениям (3) и используя
только что приведённые, получим:![]() .
Подставляя выражение для k1 в предыдущую
формулу, получим
.
Подставляя выражение для k1 в предыдущую
формулу, получим![]() ,
,
![]() ,так
как
,так
как![]() .
Тогда
.
Тогда![]() ,
где
,
где![]() .
Решаем
последнее уравнение графически. Точки
пересечения дают значения энергии. Так
как прямая неограни-но возрастает, а
синус – функция ограниченная, то число
точек пересечения будет конечно. Таким
образом, и спектр энергии будет
дискретным.
.
Решаем
последнее уравнение графически. Точки
пересечения дают значения энергии. Так
как прямая неограни-но возрастает, а
синус – функция ограниченная, то число
точек пересечения будет конечно. Таким
образом, и спектр энергии будет
дискретным.