
- •1. Фотоэффект.
- •2. Эффект Комптона.
- •3. Поляризация фотонов. Интерференция фотонов.
- •4. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •5 . Эффект Рамзауэра – Таунсенда.
- •6.Понятие волн де Бройля. Уравнения де Бройля. Эксперименты по волновой природе элементарных частиц
- •Эксперименты по волновой природе элементарных частиц.
- •7. Законы излучения абсолютно черного тела, формула Планка.
- •8. Опыт Франка-Герца. Атомные спектры.
- •9 . Опыты Резерфорда Ядерная модель атома.
- •10. Постулаты Бора...
- •11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.
- •13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •17.Частица в одномерной прямоугольной потенциальной яме конечной глубины
- •1 8.Прохождение частицы сквозь потенциальный барьер(туннельный эффект)
- •19. Контактная разность потенциалов, эффект холодной эмиссии электронов, альфа – распад.
- •20. Уравнение Шредингера для атома водорода, собственные значения и собственные функции угловой части.
- •21. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •22. Уравнение Шредингера для атомов щелочных метало, собственные значения и энергии.
- •23. Спектральные серии щелочных атомов, правила отбора
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •28.Эффект Пашена-Бака.
- •31.Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
- •32. Рентгеновские спектры.
14. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
Оператор
координаты является оператором умножения
на эту координату:
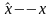 .
Например
.
Например
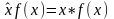
Оператор проекции импульса на оси декартовой системы координат:
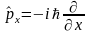 ;
;
 ;
;

Например:
Оператор полного импульса:

Оператор Гамильтона может быть получен как оператор импульса. В классической физике функцией Гамильтона называется полная энергия системы, выраженная через обобщение координаты и обобщение импульса:
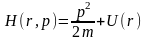 ,
где U(r)
– потенциальная энергия
,
где U(r)
– потенциальная энергия
Оператор Гамильтона:
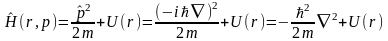
Оператор момента импульса частицы:

Операторы момента импульса:
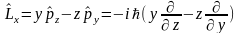
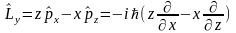


В квантовой физике величины характеризуются не числовыми значениями, а оператором. Оператор – правило, по которому каждой функции из некоторого пространства L ставится в соответствие функция из того же пространства.
В
общем случае
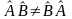 .
Если выполняется условие
.
Если выполняется условие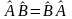 ,
то операторы
,
то операторы
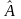 и
и
 называются коммутирующими, а запись
называются коммутирующими, а запись
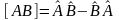 называется коммутатором операторов
и
.
называется коммутатором операторов
и
.
Если
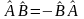 ,
то операторы
и
называются антикоммутирующими, и
запись
,
то операторы
и
называются антикоммутирующими, и
запись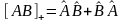
Собственные функции и собственные значения линейных операторов.
Если результатом действия оператора на функцию u является та же функция, умноженная на число λ, то число λ называется собственным значением оператора , а функция u – собственной функцией .
Собственные функции в квантовой теории должны удовлетворять условиям непрерывности, конечности, гладкости, однозначности. Совокупность собственных значений оператора называется его спектром. Именно собственные значения обнаруживаются в эксперименте.
15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
Условие одновременной измеримости различных динамических переменных:
Необходимым
и достаточным условием этого является
коммутативность соответствующих
операторов, то есть коммутатор этих
операторов должен быть равен нулю.
Например, коммутатор операторов
 и
и
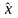 :
:

Соотношение неопределённостей Гейзенберга:
В
1927 г. В.Гейзенберг открыл так
называемые соотношения
неопределенностей, в
соответствии с которыми
неопределенности координаты и импульса связаны
между собой соотношением:
![]() ,
где
,
где ![]() , h постоянная
Планка.
Своеобразие описания микромира
в том, что произведение неопределенности
(точности определения) положения Δx и
неопределенности (точности определения)
импульса Δpx всегда
должно быть равно или больше константы,
равной –
, h постоянная
Планка.
Своеобразие описания микромира
в том, что произведение неопределенности
(точности определения) положения Δx и
неопределенности (точности определения)
импульса Δpx всегда
должно быть равно или больше константы,
равной – ![]() .
Из этого следует, что уменьшение одной
из этих величин должно приводить к
увеличению другой. Хорошо известно,
что любое измерение сопряжено с
определенными ошибками и совершенствуя
приборы измерения, можно уменьшать
погрешности, т. е. повышать точность
измерения. Но Гейзенберг показал, что
существуют сопряженные (дополнительные)
характеристики микрочастицы, точное
одновременное измерение которых,
принципиально невозможно. Т.е.
неопределенность – свойство самого
состояния, оно не связано с точностью
прибора.
.
Из этого следует, что уменьшение одной
из этих величин должно приводить к
увеличению другой. Хорошо известно,
что любое измерение сопряжено с
определенными ошибками и совершенствуя
приборы измерения, можно уменьшать
погрешности, т. е. повышать точность
измерения. Но Гейзенберг показал, что
существуют сопряженные (дополнительные)
характеристики микрочастицы, точное
одновременное измерение которых,
принципиально невозможно. Т.е.
неопределенность – свойство самого
состояния, оно не связано с точностью
прибора.
Для
других сопряженных величин – энергии E
и времени t соотношения
неопределенностей, имеет
вид:
![]() .
Это
означает, что при характерном времени
эволюции системы Δt ,
погрешность определения ее энергии не
может быть меньше чем
.
Это
означает, что при характерном времени
эволюции системы Δt ,
погрешность определения ее энергии не
может быть меньше чем ![]() . Из
этого соотношения следует возможность
возникновения из ничего, так
называемых, виртуальных
частиц на
промежуток времени меньший, чем
. Из
этого соотношения следует возможность
возникновения из ничего, так
называемых, виртуальных
частиц на
промежуток времени меньший, чем ![]() и
обладающих энергией ΔE.
При этом закон сохранения энергии не
будет нарушен. Поэтому по современным
представлениям вакуум это
не пустота, в которой отсутствуют поля
и частицы, а физическая сущность, в
которой постоянно возникают и исчезают
виртуальные частицы.Одним
из основных принципов квантовой механики
является принцип
неопределенностей, открытый
Гейзенбергом. Получение информации об
одних величинах, описывающих микрообъект,
неизбежно ведет к уменьшению информации
о других величинах, дополнительных к
первым. Приборы, регистрирующие
величины, связанные соотношениями
неопределенности, разного типа, они
дополнительны друг к другу. Под
измерением в квантовой механике
подразумевается всякий процесс
взаимодействия между классическим и
квантовыми объектами, происходящий
помимо и независимо от какого-либо
наблюдателя. Если
в классической физике измерение не
возмущало сам объект, то в квантовой
механике каждое измерение разрушает
объект, уничтожая его волновую функцию.
Для нового измерения объект нужно
готовить заново. В этой связи Н. Бор
выдвинул принцип
дополнительности,
суть которого в том, что для полного
описания объектов микромира необходимо
использование, двух противоположных,
но дополняющих друг друга представлений.
и
обладающих энергией ΔE.
При этом закон сохранения энергии не
будет нарушен. Поэтому по современным
представлениям вакуум это
не пустота, в которой отсутствуют поля
и частицы, а физическая сущность, в
которой постоянно возникают и исчезают
виртуальные частицы.Одним
из основных принципов квантовой механики
является принцип
неопределенностей, открытый
Гейзенбергом. Получение информации об
одних величинах, описывающих микрообъект,
неизбежно ведет к уменьшению информации
о других величинах, дополнительных к
первым. Приборы, регистрирующие
величины, связанные соотношениями
неопределенности, разного типа, они
дополнительны друг к другу. Под
измерением в квантовой механике
подразумевается всякий процесс
взаимодействия между классическим и
квантовыми объектами, происходящий
помимо и независимо от какого-либо
наблюдателя. Если
в классической физике измерение не
возмущало сам объект, то в квантовой
механике каждое измерение разрушает
объект, уничтожая его волновую функцию.
Для нового измерения объект нужно
готовить заново. В этой связи Н. Бор
выдвинул принцип
дополнительности,
суть которого в том, что для полного
описания объектов микромира необходимо
использование, двух противоположных,
но дополняющих друг друга представлений.
