13. Постулаты квантовой механики и описание динамических переменных с помощью операторов.

Как и любая область науки, квантовая механика базируется на нескольких основных положениях, принимаемых без доказательства. Эти основные положения сформулированы в виде постулатов.

I постулат. Состояние движения квантового объекта описывается волновой функцией .

Физический смысл волновой функции в том, что её квадрат есть плотность вероятности обнаружения частицы в данном квантовом состоянии. Плотность вероятности определяется так: 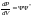, так как функция комплексна. Тогда вероятность обнаружения частицы в данном квантовом состоянии, описываемом волновой функцией, будет: .

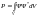II постулат. Волновая функция подчиняется волновому уравнению: .

Здесь – оператор Гамильтона (полной энергии системы), а уравнение, сформулированное во втором постулате, называется уравнением Шредингера.

III постулат. Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.

IV постулат. При иизмерении некоторой динамической переменной, описываемой оператором , с определённой вероятностью получается одно из собственных значений этого оператора. Вероятность измерения собственного значения 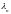равна , где 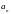есть коэффициент разложения волновой функции 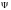по собственным функциям оператора : . Среднее значение динамической переменной, описываемой оператором в состоянии, описываемом волновой функцией , определяется так: .

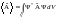Согласно третьему постулату операторы, описывающие динамические переменные, должны быть линейными и эрмитовыми. Однако третий постулат не даёт конкретных значений этих операторов. Вид основных операторов определяется так, чтобы полученные с помощью них значения, совпадали с экспериментальными. Остальные операторы получаются путём формальной замены в функции, описывающей соответствующую величину в классической физике, всех переменных на соответствующие им операторы. Необходимо следить за тем, чтобы полученный оператор оставался линейным и эрмитовым.

1. Оператор координаты есть оператор умножения на эту координату: , например, .

2. Оператор проекции импульса на оси декартовой системы координат есть , например, . Так как импульс величина векторная, то в векторной форме . Тогда, после соответствующих преобразований, получим 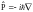. Например, .

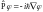3. Оператор полной энергии имеет вид: .

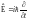4. Получим теперь уравнение для оператора . В классической физике функция Гамильтона есть полная энергия системы. Функция Гамильтона выражается через обобщённые координаты так: – сумма кинетической и потенциальной энергий. Тогда, пользуясь общим правилом, запишем оператор : 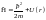, или .

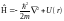5. Оператор момента импульса. В классической физике . Тогда, расписывая по координатам вектор , получим: ; и . Теперь по общему правилу, производя формальную замену, мы можем записать: 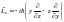, , 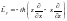. Перейдём теперь к сферической системе координат 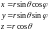(1). Теперь, производя дифференцирование, при переходе к новым переменным, получим: . Так как 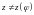, то 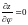. Таким образом, . Возвращаясь к формуле (1), мы можем переписать последнее уравнение: 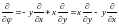. Отсюда для имеем уравнение: .
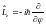