11. Спектральн. Линии. Изотопический сдвиг спектр. Линий.

Все спектры (испускания, поглощения) делятся на линейчатые, полосатые и сплошные. Чем проще структура вещества, тем разрежённей его спектр. С другой стороны, чем меньше электронов содержит вещество, тем проще его спектр. Линейчатые спектры характерны для атомов определённых веществ. Полосатые спектры дают молекулы газа в разряженном состоянии. Сплошным спектром обладает газ при высокой температуре или жидкость, а также твёрдые тела.

Проведя исследования было обнаружено: что спектральные линии объединяются в серии. Серией называется группа спектральных линий, соответствующая переходу атома с одного и того же энергетического уровня на какой-либо другой (для спектра испускания) либо в одно и то же энергетическое состояние (для спектра поглощения). Первая спектральная серия для атома водорода была обнаружена Бальмером и получила его имя. Изучая спектр атома водорода в видимой области, Бальмер получил формулу: 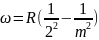где m=1, 2, 3…. Впоследствии были открыты и остальные серии для атома водорода:

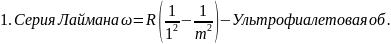
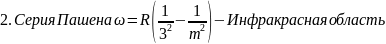
Расстояния между спектральными линиями с увеличением числа m становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий:

Причём n определяет номер спектральной серии. для спектра испускания; для спектра поглощения. Введём

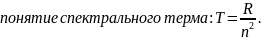
Таким образом, частота любой спектральной линии определяется Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой:

уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае

В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.Изотопами наз. элементы, заряд ядра к-ых одинаков, а массы различны. Химические св-ва изотопов весьма близки др. к др.

Дейтрон – ядро атома дейтерия, состоит из протона и нейтрона. Тритон – ядро атома трития, состоит из протона и 2-х нейтронов. Различие в массах ядер различных изотопов приводит к сдвигу линий др. относительно др. в их спектрах излучения – изотопический сдвиг. Он не велик. Например для

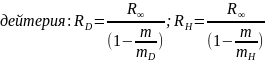
По сдвигу этих линий можно определить массу изотопа, по интенсивности – концентрацию изотопа.Две собственные ф-ции, принадлежащие различным собственным значениям, ортогональны друг другу т.е. интеграл от произведения одной из этих ф-ций на ф-цию, комплексно сопряженную с другой, взятый по всей области интегрирования равен нулю.

12. Ур-ие Шрёдингера как основа квантово-механического описания дискретных состояний атомов. Собственные значения и собственные ф-ии этого ур-ия, их свойства.

Из основных ур-ий электромагнитного поля вытекает волновое ур-ие для электромагнитных волн. Записываем и подставляем в него решение в виде плоских волн получим соотношение между частотой и составляющими волнового вектора (закон дисперсии):

Из соотношений между импульсом и энергией ньютоновской

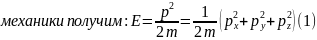
Воспользуемся квантовыми соотношениями для энергии и составляющих импульса:

Подставляя их в (1), сокращая на 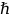получим:

- закон дисперсии волн де Бройля в нерелятивистском приближении. Далее возьмем формулу плоской волны де Бройля и продифференцировав ее 1 раз во времени и 2 по всеми координатам получим:

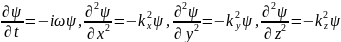
Найдя отсюда 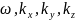и подставив в закон дисперсии (2):

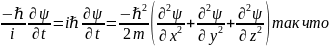
Для стоячих монохроматических волн решение может быть представлено в виде произведения 2-х ф-ий, одна из к-ых ф-ия координат, другая - ф-ия времени, зависимость от времени . Для таких решений левая часть (3) дает:

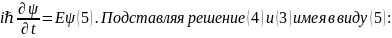
Частицы. Обобщим его на случай частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U. Полная энергия равна 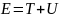. Для случая движения в поле с потенциальной энергией мы должны подставить вместо E в (6) кинетическую энергию и ур-е примет вид:

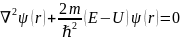
На приведенные соображения следует смотреть как на соображения, поясняющие установление ур-ия Шредингера, а не как вывод его. Вообще это ур-е строго вывода не имеет, оно устанавливается, и правильность его подтверждается согласием с опытом получаемых с его помощью результатов.

Свидетельством квантового характера ур-я Шредингера явл. Присутствие в нём постоянной Планка . Ур-е Шредингера записывается в 2-х наиболее распространённых формах.

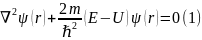
- эта форма наиболее удобна для нахождения ф-ии как решение дифференциального ур-я. Другая форма записи:

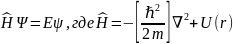
Более удобна для исследования принципиальных вопросов квантовой механики и обобщения ур-я Шредингера.

Еще есть ур-е Шредингера зависящее от времени:

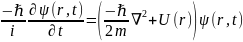
Ур-е Шредингера имеет решение не при любых значениях Е, а лишь при некоторых, к-ые обозначаем 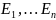. Значение Е при к-ых (1) имеет решение обладающее указанными свойствами, т.е. наз. собственными значениями, а функции 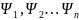явл. Решением ур-ия (1) при собственными ф-ями, принадлежащими собственным значениям .