По физической природе

• Механические (звук, вибрация)

• Электромагнитные (свет, радиоволны, тепловые)

• Смешанного типа — комбинации вышеперечисленных

По характеру взаимодействия с окружающей средой

• Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

• Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебания являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

• Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями.

• Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

• Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.

2) Гармоническое колебание. Основные параметры

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

x(t) = Asin(ωt + φ)

или

x(t) = Acos(ωt + φ),

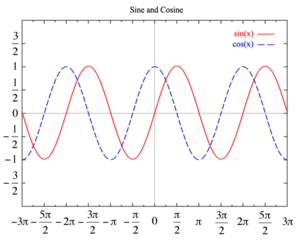
Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.

где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, (ωt + φ) — полная фаза колебаний,  — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

Постоянные величины А, Т, , входящие в уравнение (9.1), называются параметрами колебания. Рассмотрим их физический смысл.

Из (9.1) следует, что в случае, если соs(2·t/Т + ) = ± 1, то  значение модуля x максимально, т.е. |x| = x_max = A. Величину А, равную наибольшему значению колеблющейся физической величины, назовем амплитудой колебания. 

В случае изменения времени на величину, кратную T, аргумент функции косинус изменится на величину, кратную 2, а х и ее производная примут первоначальные значения:

x(t) = x(t + n·T),   (t) = (t + n·T) где Т - период, минимальное время, по истечение которого процесс колебаний  полностью повторяется$ n - целое число.

Период колебаний - наименьшее время по истечении которого движение полностью повторяется, т.е. сама колеблющаяся величина и ее скорость принимают прежние значения.

Величина, обратная периоду колебаний Т, называется частотой  = 1/Т. Частота - есть число колебаний, совершаемое системой, за 1 секунду. Циклическая или круговая частота - есть число колебаний за 2секунд w = 2/Т = 2·.

Мгновенное значение физической величины х определяется значением аргумента функции косинус, который называется фазой колебаний: 

Ф = w·t + ₀.

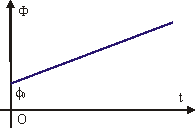Рис. 9.2. Зависимость фазы гармонических колебаний от времени.

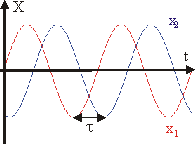Рис. 9.3.

Фаза колебаний Ф линейно растет со временем (см. рис. 9.2). При t = 0 значение Ф равняется ₀, которое называется начальной фазой колебания. Начальную фазу можно рассчитать, исходя из значения физической величины в начальный момент времени и известной амплитуды колебаний:

х(0) = х₀ = А·cos ₀;    cos ₀ = х₀/A.

Следовательно, ₀ зависит от выбора начала отсчета времени. 

Например, если для колебаний, описываемых уравнением (9.1),  x(0) = х₀ = 0, то ₀ = /2, если  x(0) = х₀ = А, то ₀ = 0.

В случае, если амплитуда колебаний не известна, то для нахождения начальной фазы и амплитуды колебаний кроме начального смещения необходимо знать начальное значение скорости колеблющегося тела. 

Большое значение для анализа сложного колебательного движения имеет понятие разности фаз двух колебаний: Ф = Ф₂ - Ф₁. Если колебания синхронные (т.е  имеют одинаковую частоту), то величина Ф не зависит от времени и они происходят с постоянным сдвигом фаз. Пример такого рода колебаний приведен на рис. 9.3. Колебание величины x₁ = A₁·sin(w·t)  опережает колебание x₂ = A₂·sin(w·(t - )).

Если колебания несинхронные, то величина Ф зависит от времени.

Синхронными называются гармонические колебания, имеющие одинаковые частоты.

Сдвиг фаз можно выразить в радианах и в долях периода. Пусть колебания подчиняются уравнениям:

x₁ = A₁·sin(2·t/T); x₂ = A₂·sin(2·(t - )/T), где  - время запаздывания 2-го колебания относительно 1-го.

Второе колебание можно представить в следующем виде:

x₂ = A₂·sin(2·t/T - 2·/T).

Очевидно, ₁ - ₂ = 2·/Т.     (9.2)

Из уравнения (9.2) следует, что если  = Т/4, то ₁ - ₂ = /2, а при  = Т/2, сдвиг фаз ₁ - ₂ = .

Рис. 9.4.

Колебания, происходящие со сдвигом фаз , называются антифазными. Имеется некоторая неопределенность в отставании и опережении на . Нельзя сказать, которое из колебание отстает, т. к. математически эти утверждения эквивалентны. Рассмотрим случай, когда х₂ отстает от х₁ больше, чем на  (см. рис. 9.4). Сдвиг по фазе Ф₁ - Ф₂ =  + ' характеризует отставание 2-го колебания от 1-го. Из графика видно, что такое отставание эквивалентно опережению 2-м колебанием 1-го на угол Ф₂ - Ф₁ =  - '. Такой же результат получим и математически, исходя из тригонометрического равенства:

sin( + ) = sin( - ).

Чтобы не было этой неопределенности, условились сдвиг фаз задавать в диапазоне от 0 до . 

Влияние параметров колебаний на их вид вы можете наблюдать на графиках, которые построите самостоятельно.