Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[1].

24) Законы динамики вращательного движения

1. Момент силы.

Вращающее действие силы определяется ее моментом. Моментом силы относительно какой-либо точки называется векторное произведение

, (40)

- радиус-вектор, проведенный из точки в точку приложения силы (рис.5). Единица измерения момента силы .

Величина момента силы

,

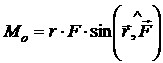или можно записать

, (41)

где - плечо силы ( кратчайшее расстояние от точки до линии действия силы).

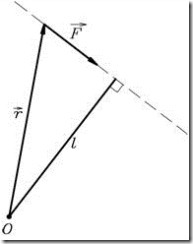
Рис.5.

Момент силы относительно какой-либо точки равен нулю, если линия действия силы проходит через эту точку.Проекция вектора на какую-либо ось, например, ось z, называется моментом силы относительно этой оси. Чтобы определить момент силы относительно оси, сначала проецируют силу на плоскость, перпендикулярную оси (рис.6), а затем находят момент этой проекции относительно точки пересечения оси с перпендикулярной ей плоскостью. Если линия действия силы параллельна оси, или пересекает ее, то момент силы относительно этой оси равен нулю.

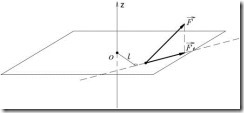
Рис.6.

2. Момент инерции тела.

Моментом инерции тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси

, (42)

- масса -той точки , - кратчайшее расстояние от -той точки до оси z.

Для сплошных тел момент инерции определяется через интеграл

, (43)

- расстояние от элемента массы тела до оси z.

Моменты инерции однородных тел простой геометрической формы обычно рассчитывают по формуле (43), а сложной определяют экспериментально. В таблице 1 приведены моменты инерции некоторых тел.

Теорема Штейнера. Если для какого-либо тела известен его момент инерции относительно оси , проходящей через центр масс тела, то момент инерции этого тела относительно оси , параллельной , равен

, (44)

- масса тела, - кратчайшее расстояние между осями и .