1) Механическое движение. Системы отсчёта. Пространство и время и их физические свойства. Принцип относительности в механике Простейшей формой движения является механическое движение, которое заключается в изменении с течением времени положения тел или их частей относительно друг друга. Совокупность неподвижных относительно друг друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчёта. Движение одного и того же тела относительно различных систем отсчёта может иметь различный характер. Для примера представим себе набирающий скорость поезд. Пусть по коридору одного из вагонов этого поезда идёт с постоянной скоростью пассажир. Тогда движение пассажира относительно вагона будет равномерным, а относительно поверхности Земли – ускоренным. Движение тел происходит в пространстве и во времени. Ньютон считал пространство и время абсолютными, не зависящими как друг от друга, так и от присутствующих в пространстве тел. Абсолютное пространство определялось Ньютоном как безотносительное к чему-либо внешнему вместилище вещей, остающееся всегда одинаковым и неподвижным. О времени Ньютон писал: «абсолютное истинное или математическое время само по себе и в силу своей внутренней природы течёт равномерно, безотносительно к чему-либо внешнему». Теория относительности внесла в представления о пространстве и времени коренные изменения. Согласно СТО (специальная теория относительности) пространство и время неразрывно связаны друг с другом, образуя единое четырёхмерное пространство-время. Из общей теории относительности следует, что присутствие гравитирующих (тяготеющих) масс «искривляет» пространство и оказывает влияние на ход времени.

2) Измерение интервалов времени и длины. Собственное время, собственная длина.

СОБСТВЕННОЕ ВРЕМЯ - время, измеряемое часами, движущимися вместе с рассматриваемым телом, т. е. время в собственной системе отсчёта. Время протекания к--л. процесса, измеряемое внеш. наблюдателем, мимо к-рого движется тело, зависит от относит. скорости движения. Если измерения проводятся наблюдателем в инерциальной системе отсчёта, то собств. промежуток времени протекающий на движущемся теле, связан с временем t системы отсчёта ф-лой:

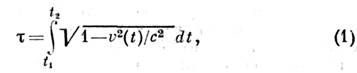
где v(t) - скорость движения тела. Промежуток С. в. является длиной отрезка мировой линии данного тела, делённой на с. В общем случае при измерении времена в произвольной (неинерциальной) системе отсчёта и при наличии полей тяготения ф-ла (1) заменяется след. выражением:

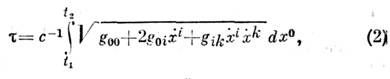
где g₀₀, g_0i, g_ik, - компоненты фундаментального метрич. тензора (по дважды встречающимся индексам подразумевается суммирование i, k = 1, 2, 3), x⁰ = ct, xⁱ - компоненты скорости движения тела. Если тело покоится в статич. слабом поле тяготения, то ф-ла (2) принимает вид:

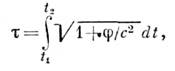
где - ньютоновский потенциал поля тяготения. Т.к. , то С. в. в поле тяготения течёт медленнее, чем вне его. См. Относительности, теория, Тяготение. И. Д. Новиков.

Собственная длина стержня.

Собственная длина стержня - длина стержня в той системе отсчета, в которой он покоится. В этой системе собственная длина стержня максимально по сравнению с длиной того же стержня, измеренной в любой другой системе отсчета, движущейся вдоль этого стержня.

3) Виды механического движения. Модели в механике: модель материальной точки, абсолютно твёрдого тела, сплошной среды.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково. Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение. Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось. Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное. Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях. Например, колебательное движение совершает маятник в часах. Поступательное и вращательное движения – самые простые виды механического движения.

Движение тел происходит под действием сил. Под действием внешних сил тела могут деформироваться, т.е. изменять свои размеры и форму.        Тело, деформацией которого можно пренебречь в условиях данной задачи, называют абсолютно твердым телом (хотя абсолютно твердых тел в природе не существует).        Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой. В механике сплошных сред на основе методов, развитых в теоретической механике, рассматриваются движения таких материальных тел, которые заполняют пространство непрерывно, пренебрегая их молекулярным строением. Вместе с тем также считаются непрерывными характеристики тел, такие, как плотность, напряжения, скорости и т. д.