Вопрос № 43: Понятие о функциях, заданных неявно:

1. Понятия о функциях, заданных неявно.

   1. Их дифференцирование.

2. Касательная плоскость.

3. Нормаль к поверхности.

Касательная и нормаль к поверхности:

В случае явного указания поверхности, то есть , где существует и непрерывна в области точки , тогда: – приращение аппликаты касательной плоскости, при переходе от точки на касательной плоскости в точку .

В случае неявного задания функции – , если при этом выполняется условие о неявно заданной функции, то вблизи функции ????

Тогда уравнение касательной плоскости выглядит так: учитывая формы для в случае неявного задания:

Назовём нормалью к поверхностью прямую, перпендикулярную касательной плоскости в любой точке:

Вопрос № 44: Частные производные высших порядков:

1. Частные производные высших порядков.

2. Независимость смешанных производных от порядка дифференцирования.

3. Дифференциалы высших порядков.

4. Формула Тейлора для функции многих переменных.

Вообще частные производные порядка к от функции , где – называется производная от производной к-1-ого порядка по каждой из переменной.

Определение: имеет частные производные по х, то есть существуют , то её называют производной второго порядка для функции и обозначают , аналогично

Теорема о смешанных производных:

Пусть для существуют частные производные первого порядка, тогда:

Заметим, что для элементарных функций смешанные производные так же элементарные функции.

Дифференциалы высших порядков:

Для функции существует непрерывная производная второго порядка. Вторым дифференциалом функции называется дифференциал от первого дифференциала функции.

Используя метод математической индукции можно доказать, что н-ного порядка:

Формула Тейлора:

существует в окрестности точки непрерывна производная до п-1-ого порядка включительно, тогда

Вопрос № 45: Экстремум функции многих переменных:

1. Экстремум функции многих переменных.

2. Необходимое условие существования экстремума.

3. Формулировка достаточных условий существования экстремума.

Говорят, что для функции существует минимальное (максимальное) значение в точке М⁰ из области определения, если у М⁰ существует окрестность, во всех точках которой: , или приращение функции меньше нуля, для максимума, и больше для минимума.

Необходимое условие существования экстремума:

Экстремум функции существует только тогда, когда существуют и равны нулю первые частные производные по всем переменным функции.

Доказательство:

– это функция одной переменной х₁, которая в точке ; Существует экстремум, отсюда, как известно для функции одной переменной её производная по переменной х₁⁰ в точке равна нулю. Это частная производная функции по переменной х₁, для

Такая точка называется стационарной.

Следствие:

В стационарной точечке производная функции равна нулю, вектор градиента функции в стационарной точке равен нулевому вектору.

Все стационарные точки являются точками возможного экстремума, в этой точке рассматривается достаточное условие экстремума.

Функция в окрестности стационарной точки, частные производные второго порядка непрерывны:

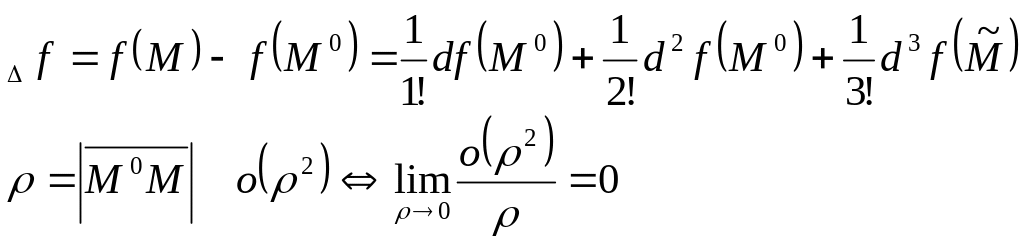
– то есть знак приращения определяется знаком второго дифференциала. Выражение такого вида, где называется квадратичной формой.

Для определения знака квадратичной формы используется критерий Сильвестра.

Рассмотрим , вычислим его главные миноры.

1. Если все миноры больше нуля, то квадратичная форма является положительно определённой, функция имеет минимум в точке.

2. Если идёт чередование знаков, причём первый минор отрицателен, то квадратичная форма является отрицательно определённой, функция имеет минимум в точке.

3. При любых других расстановках знаков у миноров квадратичная форма является неопределённой по знаку, и функция не имеет в точке экстремума.

4. Если квадратичная форма равна нулю, при условии, что не все приращения равны нулю, то для исследования на экстремум следует применять производные более высоких порядков.