Вопрос № 18: Понятие сложной функции:

1. Понятие сложной функции.

2. Непрерывность сложной функции в точке.

Пусть определена на , и определена на , тогда на определена следующая функция – суперпозиция функций.

Если непрерывна в и непрерывна в , то непрерывна в точке а.

Заметим, что основные элементарные функции непрерывны в каждой точке своей области определения. Все элементарные функции непрерывны в своей области определения.

Вопрос № 19: Классификация точек разрыва:

1. Классификация точек разрыва.

2. Понятие кусочно-непрерывной функции.

Точка называется точкой разрыва, если в ней нарушается определение непрерывности функции. Точки разрыва делятся на две категории:

0. Если существуют односторонние конечные пределы в точке, то точку называют точкой разрыва первого рода, в частном случае, если конечны односторонние пределы, то точку называют точкой устранимого разрыва.

1. Если хотя бы один из односторонних пределов бесконечен, или не существует, то точку называют точкой разрыва второго рода.

Функция непрерывна на отрезке А-В, если она непрерывна на интервале А-В, а так же существует и конечна (непрерывность справа), а так же существует и конечна (непрерывность слева).

кусочно-непрерывна на отрезке А-В, если она непрерывна на интервале А-В, за исключением конечного числа точек разрыва первого рода, и существуют конечные правый и левый пределы.

Вопрос № 20: Комплексные числа:

1. Комплексные числа.

2. Комплексная плоскость.

3. Операции над комплексными числами в алгебраической форме.

Число вида: , где х,у – действительные числа, а i – число, квадрат которого даёт минус единицу – мнимая единица!

– сопряжонное.

Арифметические действия над комплексными числами:

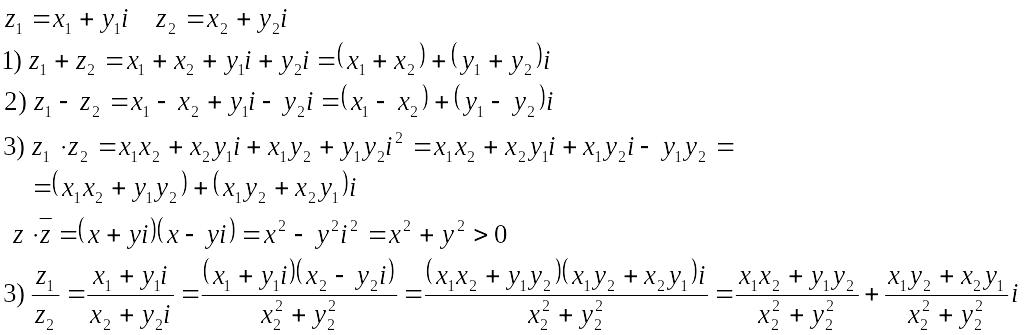
Степени числа i:

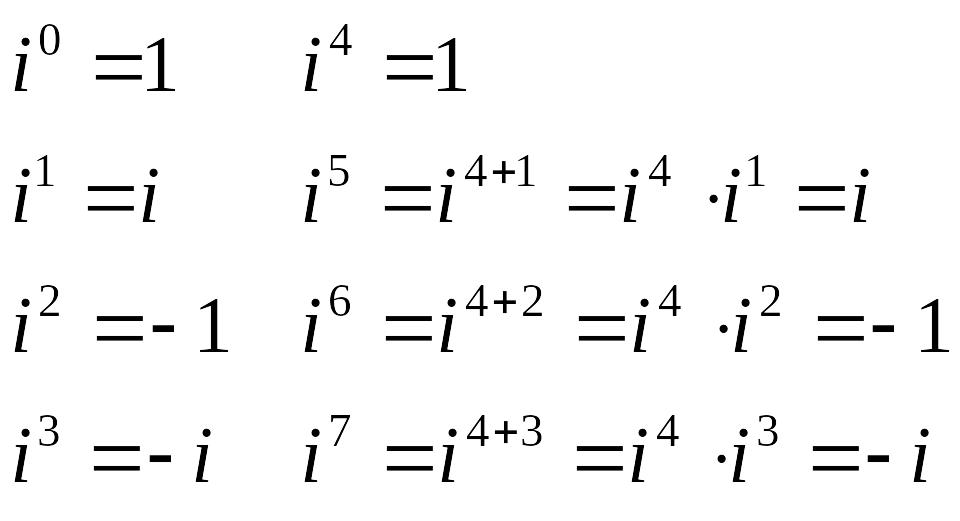
Вопрос № 21: Тригонометрическая форма записи комплексных чисел:

1. Тригонометрическая форма записи комплексных чисел.

2. Возведение в степень.

3. Извлечение корня.

Комплексное число характеризуется упорядоченной парой чисел, ей соответствует единичная точка на плоскости при выбранной системе координат. Говорят, что она изображает комплексное число, а координатную плоскость называют комплексной плоскостью. На плоскости совмещены полярная и декартова система координат так, что полюс полярной системы совпадает с началом декартовой системы координат, а полярная ось совпадает с осью ОХ.

Задаются радиус – то есть модуль комплексного числа и угол φ равный арктангенсу отношения мнимой части комплексного числа к его действительной части.

Тогда комплексное число будет выглядеть так:

Формула Эйлера:

Возведение в степень:

Извлечение корня:

Введём понятие всех значений: , тогда

Вопрос № 22: Производная функции одной переменной:

1. Производная функции одной переменной.

2. Геометрическая интерпретация.

3. Уравнение нормали и касательной к графику.

Пусть определена на интервале А-В. Фиксированной точке х придадим приращение так, что бы точка принадлежала интервалу А-В.

– приращение функции в точке х, соответствует приращению у.

Придел разности отношения приращения функции к приращению аргумента, при стремлении последнего к нулю называется производной функции в точке х.

Физический смысл:

Пусть закон прямолинейного движения точки по прямолинейному пути.

Отношение приращений функции к аргументу – средняя скорость движения за время _Δх, а производная – мгновенная скорость в точке.

Геометрический смысл:

– производная – тангенс угла наклона касательной, к прямой в точке, к оси абсцисс.

Уравнение касательной и нормали:

Возьмём на касательной произвольную точку, тогда: – верно для любой точки на касательной .

Прямая, перпендикулярная касательной называется нормалью к графику в точке. Известно, что у перпендикулярных прямых угловые коэффициенты связаны следующим образом: , следовательно уравнение нормали будет выглядеть следующим образом: .

Вопрос № 23: Правила дифференцирования:

1. Правила дифференцирования суммы.

   1. разности.

   2. произведения.

   3. частного.

Пусть функции имеют конечные производные, тогда:

Докажем, что производная суммы – есть сумма производных:

Вопрос № 24: Производная сложной и обратной функции:

1. Производная сложной функции.

2. Производная обратной функции.

3. Логарифмическая производная.

Если для всех значений функции из области её определения можно поставить в соответствие единственный х из области определения функции: , то говорят, что на множестве задана обратная функция с областью определения и областью значения

Теорема о существовании обратной функции:

определена, непрерывна и возрастает (убывает) в окрестности точки х₀, где , тогда в окрестности определена обратная функция – непрерывная монотонная и имеющая в точке у₀ производную, равную

Производная сложной функции:

Пусть имеет в точке и конечную производную, а имеет в точке х конечную производную, тогда имеет в точке х конечную производную:

Логарифмическая производная:

Пусть больше нуля и имеет в точке х производную, тогда:

– логарифмическая производная

Вопрос № 25: Параметрическое дифференцирование, производные высших порядков:

– в свою очередь то же является функцией, если для в точке х существует производная, то её называют производной второго порядка.

Аналогично

Параметрическое дифференцирование:

Пусть х(t) и у(t) имеют в точке t производную, при этом функция х(t) имеет обратную функцию в окрестности рассматриваемой точки, тогда существует производная , которая вычисляется по формуле:

Действительно , где обратная к

Вопрос № 26: Понятие дифференцируемой функции в точке х:

1. Понятие дифференцируемой функции в точке х.

2. Теорема о дифференцируемой функции.

– называется дифференцируемой в точке х, если приращение функции представимо в виде: , где А – независимо от приращения аргумента, а α стремится к нулю, при стремлении приращения аргумента к нулю.

Утверждение: Если функция дифференцируема в точке, то она непрерывна в ней. Действительно при стремлении приращений функции и аргумента к нулю, что и означает непрерывность функции в точке.

Дифференциал функции – это производная функции, умноженная на дифференциал аргумента.

Для дифференцируемости функции в точке необходимо и достаточно существование в этой точке конечной производной.

Вопрос № 27: Понятие дифференциала:

1. Понятие дифференциала.

   1. Геометрический смысл дифференциала.

2. Формула для вычисления дифференциала

Учитывая, что независимая переменная совпадает с dx:

Геометрический смысл дифференциала:

Рассматривается треугольник, построенный на касательной к графику.

Отношение катетов прямоугольного треугольника, катетами которого являются приращения функции и аргумента. Отсюда отношение катетов будет равно: приращение функции:

Производная ординаты касательно при переходе от точки х к точке x+dx равна величине дифференциала.

Формулы вычисления дифференциалов:

Если , то можно получить следующие свойства дифференциала:

Пусть дифференцируемы в точке х, тогда

Вопрос № 28: Дифференциал сложной функции:

1. Дифференциал сложной функции.

2. Инвариантность формы первого дифференциала.

. Пусть , где , причём дифференцируема в точек t, тогда: дифференцируема в точке , тогда по теореме о сложной функции для .

Заметим, что t независимая переменная для , тогда формула дифференциала для

Формула совпадает для независимых переменных х, это свойство называется инвариантностью формы записи дифференциала.

Вопрос № 29: Дифференциалы высших порядков:

1. Дифференциалы высших порядков.

2. Нарушение инвариантности формы записи второго дифференциала.

Дифференциалом второго порядка называется дифференциал от первого дифференциала.

Вычислим , когда х неизвестная переменная.

Ясно, что

Рассмотрим :

Из полученного результата видно, что второй дифференциал не обладает свойством инвариантной формы записи.

Вопрос №29: Правило Лопиталя, Формула Тейлора:

Правило Лопиталя:

Пусть дифференцируемы в окрестности точки а, за исключением быть может самой точки, и .

Пусть , тогда если существует , то существует и , и тогда . Аналогичное утверждение имеет место, когда предел функции стремится к бесконечности.

Пример:

Формула Тейлора:

Пусть дифференцируема в окрестности точки х₀ раз, то есть имеет производную до п минус первого порядка включительно, тогда для всех точек х из этой окрестности выполняется следующее:

1. – Форма Лагранжа.

2. – Форма Плана

Частным случаем формы Тейлора является формула Макларена, когда х₀=0:

Вопрос № 31: Возрастание, убывание функции в точке:

1. Возрастание функции в точке.

2. Убывание функции в точке.

3. Достаточное условие.

Функция существует в окрестности точки и дифференцируема в ней.

Говорят, что функция возрастает в точке с, если для , а для , и убывает, если , а для .

Достаточное условие возрастания и убывания функции:

0. Если существует первая производная функции в точке, и она больше нуля, то это означает, что для каждого тогда если

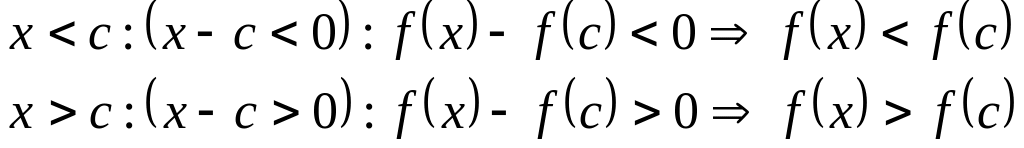
1. Если существует первая производная функции в точке, и она меньше нуля, то это означает, что для каждого *

Функция возрастает на интервале а-в, если она возрастает в каждой точке этого интервала, тогда ясно, что первая производная больше нуля, для х из этого интервала. Следовательно функция возрастает на интервале, если первая её производная больше нуля, и убывает на интервале, если первая производная меньше нуля.

Функция возрастает (убывает) на интервале, если для каждой пары точек х_1,2 из интервала, таких, что первая меньше (больше) второй, значение функции в первой точке меньше (больше), чем во второй.