Вопрос 19.Бесконечно большие и бесконечно малые последовательности. Основные свойства б.М. Последовательностей.
Величина xn называется б.б, если для любого наперед заданного числа M>0 можно указать такое натуральное число N, что для всех номеров n>N выполняется неравенство | xn|>M
а)Переменная величина xn называется б.м., если для всякого наперед заданного положительного числа Е можно узнать такое натуральное число N, что | xn|<E, для всех n>N
б) Если xn
имеет предел
0, т.е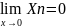
,
то такая величина называется называется
б.м.в.
Свойства б.м.в.:
1)
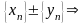0 - б.м.п.
2)
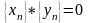
3)А*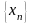
=0
4)
=
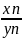б.м.в или конечная величина или const
Вопрос 20: Сходимость числовых последовательностей. Основные свойства сходящихся последовательностей. Предельный переход в неравенства.
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел.
Хn = f(n), n€N, an = f(n)
Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.
Пусть дано U1,U2…Un = fn – бесконечная числовая последовательность, тогда выражение U1 + U2 +…+ Un…+… - называется бесконечным числовым рядом. Каждый элемент Un имеет последующий элемент Un+1/ Это объясняет употребление термина «последовательность».
U1, U2 – члены числового ряда.
Un = f(n) – общий член ряда.
Если все члены ряда числа, то ряд называется числовым. Если же они являются функциями, то ряд называется функциональным.
Ряд считается законченным, если известен общий член ряда yn, выраженный как функция его номера, т.е. Un = f(n).
Сумма n-первых членов находится по формуле :
Sn = a(1 – q в степени n)/1 – q.
Геометрический ряд сходится к сумме: Sn = a/1 – q; При |q| < 1 и расходится при |q| >=1.
Если ряд U1 + U2 +…+ Un…+… сходится, то предел его общего члена Un при n →∞ равен 0.
Несмотря на то, что необходимый признак сходится, гармонический ряд расходится.
Суммой
последовательностей
и
называют последовательность
,
где
,
т.е.
.
Разностью
этих последовательностей называют
последовательность
,
где
,
т.е.
.
Если
и
‑ постоянные,
то последовательность
,
называют линейной
комбинацией
последовательностей
и
,
т.е
.
Произведением
последовательностей
и
называют последовательность с
-м
членом
,
т.е.
.
Если
,
то можно определить частное
.
Сумма, разность, произведение и частное последовательностей и называются их алгебраическими композициями.
Сходящиеся последовательности
Говорят, что
последовательность
сходится, если существует число
такое, что для любого
существует такое
,
что для любого
,
выполняется неравенство:
.
Число
называют пределом
последовательности
.
При этом записывают
или
.
Теорема.
Для того
чтобы последовательность
имела предел, необходимо и достаточно
чтобы
,
где
– постоянная;
–
бесконечно малая.
Основные свойства сходящихся последовательностей:
1Теорема: Сходящаяся последовательность имеет только 1 предел.
2Теорема: Восходящаяся последовательность ограничена.
3Теорема: Сумма(разность) 2-х сходящихся последовательностей есть последовательность сходящаяся и ее предел равен сумме(разности) пределов последовательности.
4Теорема: Произведение сходящихся последовательностей есть последовательность сходящаяся, предел которой равен произведению пределов последовательностей.
5Теорема: Отношение.
Теорема.
Если
последовательность
монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.