
- •1.Задача о вычислении объема цилиндрического тела. Двойной интеграл.
- •2.Свойства двойного интеграла
- •1. Геометрический смысл двойного интеграла.
- •6. Оценка двойного интеграла снизу и сверху: если , то где s - площадь области d.
- •3.Замена переменных в двойном интеграле.
- •4.Вычисление двойного интеграла в Декартовой системе координат.
- •1.Вычисление двойного интеграла в декартовой системе координат для правильной области
- •2. Вычисление двойного интеграла в декартовой системе координат для неправильной области
- •5.Вычисление двойного интеграла в полярной системе координат.
- •6.Тройной интеграл.
- •7.Свойства тройного интеграла.
- •2.11. Свойства тройного интеграла
- •8. Вычисление тройного интеграла в Декартовой системе координат.
- •9.Вычисление тройного интеграла в цилиндрической системе координат.
- •10. Вычисление тройного интеграла в сферической системе координат
- •11.Скалярное поле. Поверхности и линии уровня скалярного поля.
- •12.Производная по направлению скалярного поля.
- •13.Градиент скалярного поля, его свойства
- •14.Векторное поле. Векторные линии векторного поля.
- •15.Поверхностный интеграл первого рода, его свойства.
- •16.Методы вычисления поверхностного интеграла первого рода.
- •17.Поток векторного поля, его гидродинамический смысл.
- •18.Поверхностный интеграл второго рода, его свойства.
- •19.Связь между поверхностными интегралами первого и второго родов.
- •20.Вычисление потока векторного поля через замкнутую поверхность. Теорема Остроградского-Гаусса.
- •2) Если функцию f(X,y,z) интерпретировать как плотность распределения вещества вдоль дуги ав, то - масса дуги ав.
- •22.Вычисление криволинейного интеграла первого рода.
- •24.Криволинейный интеграл второго рода, его свойства.
- •4) Составим интегральную сумму вида
- •25.Вычисление криволинейного интеграла второго рода.
- •26. Формула Грина
- •27.Условия независимости криволинейного интеграла от пути интегрирования.
- •2) Интеграл не зависит от формы пути интегрирования, а зависит лишь от положения точек m0 и м;
- •4) В каждой точке области d.
- •28.Циркуляция вектора. Теорема Стокса.
- •29. Числовой ряд. Сходимость числового ряда
- •32. Необходимое условие сходимости числового ряда.
- •33. Знакоположительные числовые ряды. Признаки сравнения.
- •35. Радикальный признак Коши
- •36. Интегральный признак Коши
- •37. Знакопеременные числовые ряды. Абсолютная и условная сходимость.
- •38. Достаточный признак сходимости знакочередующегося числового ряда (Теорема Лейбница)
- •39. Функциональный ряд. Область сходимости функционального ряда.
- •40. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •1) Если степенной ряд сходится при некотором значении , то абсолютно сходится при всяком значении , для которого справедливо .
- •2) Если степенной ряд расходится при некотором значении , то он расходится при всяком : .
- •41. Свойства степенных рядов.
- •1) Если степенной ряд сходится при некотором значении , то абсолютно сходится при всяком значении , для которого справедливо .
- •2) Если степенной ряд расходится при некотором значении , то он расходится при всяком : .
- •42. Ряды Тейлора и Маклорена. Разложение функций в ряд Тейлора.
17.Поток векторного поля, его гидродинамический смысл.
Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.
Пусть поверхность S расположена в поле скоростей частиц несжимаемой жидкости с плотностью ρ=1.
Можно
показать, что поток векторного поля в
этом случае равен
![]()
где
![]() -
единичный нормальный вектор к поверхности
S,
расположенный по одну сторону с вектором
,
а величина
-
единичный нормальный вектор к поверхности
S,
расположенный по одну сторону с вектором
,
а величина
![]() .
Независимо
от физического смысла вектора
,
интеграл (3.34) по поверхности называют
потоком
векторного поля
через поверхность S.
Пусть
.
Независимо
от физического смысла вектора
,
интеграл (3.34) по поверхности называют
потоком
векторного поля
через поверхность S.
Пусть
![]() и
и
![]() ,
тогда поток П
вектора
через поверхность S
можно записать в виде:
,
тогда поток П
вектора
через поверхность S
можно записать в виде:
![]()
Или
учитывая связь поверхностных интегралов
первого и второго родов, можно записать
поток П
через поверхностный интеграл в
координатах:
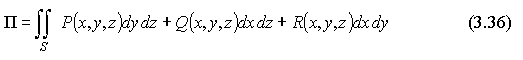
18.Поверхностный интеграл второго рода, его свойства.
Пусть задана поверхность S, ограниченная линией L (рис. 3.10).
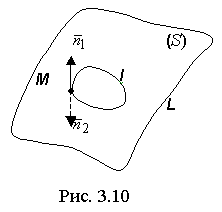
Возьмём на поверхности S какой-нибудь контур l, не имеющий общих точек с границей L.
В
точке М
контура l
можно восстановить две нормали
![]() и
и
![]() к
поверхности S.
к
поверхности S.
Выберем какое-либо одно из этих направлений.
Обводим точку М по контуру l с выбранным направлением нормали.
Если в исходное положение точка М вернётся с тем же направлением нормали (а не с противоположным), то поверхность S называют двусторонней.
Мы будем рассматривать только двусторонние поверхности Двусторонней поверхностью является всякая гладкая поверхность с уравнением z = f(x,y).
Пусть S - двусторонняя незамкнутая поверхность, ограниченная линией L, не имеющей точек самопересечения. Выберем определённую сторону поверхности.
Будем называть положительным направлением обхода контура L такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остаётся слева.
Двусторонняя поверхность с установленным на ней таким образом положительным направлением обхода контуров называется ориентированной поверхностью.
Перейдём к построению поверхностного интеграла второго рода. Как при изучении криволинейных интегралов второго рода рассматривалась направленная кривая, так и при построении поверхностного интеграла второго рода рассматривается определенная сторона поверхности.
Возьмём в пространстве двустороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан уравнением вида z = f(x,y) или является цилиндрической поверхностью с образующими, параллельными оси Oz.
Пусть R(x,y,z) - функция, опредёленная и непрерывная на поверхности S. Сетью линий разбиваем S произвольным образом на n "элементарных" участков ΔS1, ΔS2, ..., ΔSi, ..., ΔSn, не имеющих общих внутренних точек.
На каждом участке ΔSi произвольным образом выберем точку Mi(xi,yi,zi) (i=1,...,n). Пусть (ΔSi)xy - площадь проекции участка ΔSi на координатную плоскость Оху, взятая со знаком "+", если нормаль к поверхности S в точке Mi(xi,yi,zi) образует с осью Oz острый угол, и со знаком "-", если этот угол тупой.
Составим
сумму
 которую называют интегральной
суммой
для функции R(x,y,z)
по поверхности S
по переменным х,
у.
которую называют интегральной
суммой
для функции R(x,y,z)
по поверхности S
по переменным х,
у.
Обозначим λ - наибольший из диаметров ΔSi (i = 1, ..., n).
Если
существует конечный предел
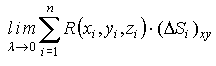 ,
,
не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек Mi ΔSi (i = 1, ..., n), то он называется поверхностным интегралом по выбранной стороне поверхности S от функции R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается

Аналогично можно построить поверхностные интегралы по координатам x, z илиу, z по соответствующей стороне поверхности, т. е.
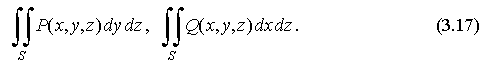
Если существуют интегралы (3.16) и (3.17), то можно ввести "общий" интеграл по выбранной стороне поверхности:
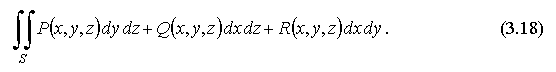 Поверхностный
интеграл второго рода обладает обычными
свойствами интеграла. Заметим лишь, что
любой поверхностный интеграл второго
рода изменяет знак при перемене стороны
поверхности.
Поверхностный
интеграл второго рода обладает обычными
свойствами интеграла. Заметим лишь, что
любой поверхностный интеграл второго
рода изменяет знак при перемене стороны
поверхности.
Вычисление интеграла (3.16) как правило, сводят к вычислению двойного интеграла.
Пусть S - двусторонняя поверхность, заданная уравнением z=f(x,y), где f(x,y) непрерывна в области τ (τ есть проекция поверхности S на координатную плоскость Оху), и R(x,y,z) - непрерывная функция на поверхности S.
Выберем "верхнюю" сторону поверхности S, тогда знак проекции (ΔSi)xy всегда "+", поэтому
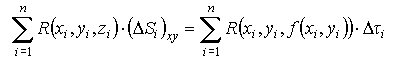 есть
интегральная сумма для функции
R(x,y,f(x,y))
по плоской области τ.
есть
интегральная сумма для функции
R(x,y,f(x,y))
по плоской области τ.
Переходя
к пределу (при
λ
0
), получаем
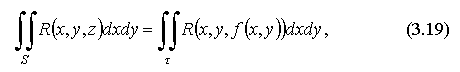 отсюда
и очевидны условия существования
поверхностного интеграла второго рода.
отсюда
и очевидны условия существования
поверхностного интеграла второго рода.
*************************************
