38. Достаточный признак сходимости знакочередующегося числового ряда (Теорема Лейбница)

Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. (1)

где для всех (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).

Теорема Лейбница. Если в знакочередующемся ряде (1) члены таковы, что

                                                                            (2)

И

           (3)

то ряд (1) сходится, его сумма положительна и не превосходит первого члена.

Док-во. Рассмотрим сумму n = 2m первых членов ряда (1):

S2m =(u₁-u₂)+ (uᴣ - u4 )+…+ (u2m-1 – u2m )

Из условия (2) следует,что выражение в каждой скобке положительно.Следовательно, сумма S2m >0

и возрастает с возрастанием m. Запишем теперь эту же сумму так:

S2m =u₁-(u₂ - uᴣ )- (u4 – u5 )-… (u2m-2 – u2m-1 )- u2m.

В силу условия (2) каждая из скобок положительна. Поэтому в результате вычитания этих скобок ui мы получим число, меньшее ui , т.е. S2m ˂ ui

Таким образом, мы установили, что S2m при возрастании mвозрастает и ограничена сверху. Отсюда следует, что S2m имеет предел S: = S, причем О < S< ui

Однако сходимость ряда еще не доказана; мы доказали только, что последовательность «четных» частичных сумм имеет пределом число S. Докажем теперь, что «нечетные» частичные суммы также

стремятся к пределу S.

Рассмотрим для этого сумму n = 2m +1 первых членов ряда (1): S2m+1 = S2m + U2m+1

Так как по условию (3) = 0, то, следовательно

= : + = : =

Тем самым мы доказали, что : = S как при четном n так и при нечетном n. Следовательно, ряд (1) сходится.

Замечание 1 Теорема Лейбница справедлива, если неравенства (2) выполняются, начиная с некоторого номера N.

Замечание 2 Теорема Лейбница иллюстрируется геометрически следующим образом. На числовой прямой будем откладывать (рис.1)частичные суммы:

, , , , …

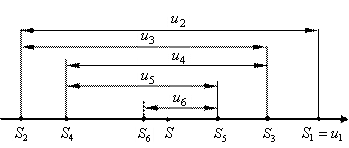
Рис. 1. Геометрический смысл теоремы Лейбница

Тогда точки, соответствующие частичным суммам будут приближаться к некоторой точке S. При этом точки, соответствующие чётным суммам располагаются слева от S, а нечетным суммам – справа от S.

Замечание 3. Если знакочередующийся ряд удовлетворяет условию теоремы Лейбница, то нетрудно оценить погрешность, которая получится, если заменить его сумму S частичной суммой Sn. При такой замене мы отбрасываем все члены ряда, начиная с Но эти числа сами образуют знакочередующийся ряд, сумма которого по абсолютной величине меньше первого члена этого ряда (т. е. меньше ). Значит, погрешность, получающаяся при замене S на Sn., не превосходит по абсолютной величине первого из отброшенных членов.

39. Функциональный ряд. Область сходимости функционального ряда.

Ряд называется функциональным, если его члены являются функциями от х, т.е . ,   , которые определены на некотором множестве X.

Если переменной  придавать различные числовые значения, то будут получаться сходящиеся или расходящиеся числовые ряды. Совокупность таких значений переменной х, при которых функциональный ряд сходится, называют областью сходимости. Областью сходимости ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.

По аналогии с числовыми рядами определяются частичные суммы функционального ряда, предел которых определяет сумму ряда (если существует). Очевидно, что сумма функционального ряда в области сходимости является функцией от х, т.е.

.

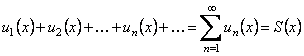Говорят, что последовательность функций  сходится равномерно к функции  на множестве D, если для любого  можно определить такой номер N, зависящий только от , что для любого  и для всех  выполняется неравенство

.

Ряд 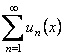 сходится равномерно на множестве D к сумме , если последовательность его частичных сумм  сходится равномерно на множестве D к функции .