6. Оценка двойного интеграла снизу и сверху: если , то где s - площадь области d.

Теорема

(О среднем значении для двойного интеграла).

Если f(x;y) - непрерывна на замкнутой области D, то существует - некая "средняя" точка области:

Доказательство Если f(x;y) непрерывна на D, то существуют наименьшее m и наибольшее М значения функции f(x;y), т.е.   по свойству 6 имеем: то есть число I/S находится между m и М.

Но непрерывная функция f(x;y) принимает все промежуточные от m до М значения существует точка : ,и теорема 2.2 доказана.

******************

3.Замена переменных в двойном интеграле.

Теорема.

Пусть двойной интеграл преобразуется от прямоугольных декартовых координат (x,y) к криволинейным u и v, связанными с прямоугольными соотношением

x=φ(u,v)

y=ψ(u,v)

где φ(u,v) и ψ(u,v) – функции устанавливающие взаимно однозначное соответствие между областью D плоскости Oxy и областью G плоскости Ouv, непрерывные вместе со своими частными производными первого порядка в области G, причем определитель преобразования (определитель Якоби)

в области G, тогда имеет место следующее соотношение

- формула замены переменных в двойном интеграле.

4.Вычисление двойного интеграла в Декартовой системе координат.

1.Вычисление двойного интеграла в декартовой системе координат для правильной области

Теорема

 Пусть область D - правильная в отношении оси Ох (рис. 2.6.) Тогда в этом случае область D может быть задана одной системой неравенств:

Если существует двойной интеграл (это возможно, например, если f(x;y) непрерывна на D), то его можно вычислить через повторный кратный интеграл так: 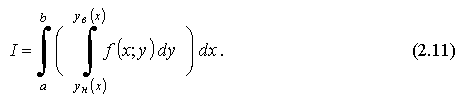При этом внутренний интеграл по у находится при постоянном х.

Данное представление (2.11) получается из определения двойного интеграла при специальном способе разбиения области D на n "мелких" частей (линиями, параллельными либо Ох, либо Оу - прямоугольной "шахматной" сеткой. А затем выполняется суммирование "объёмов" ΔV_i сначала по оси Оу, а затем по оси Ох).

2. Вычисление двойного интеграла в декартовой системе координат для неправильной области

  Если область D является неправильной в отношении обеих осей, то ее разбивают на конечное число правильных областей.

********************

5.Вычисление двойного интеграла в полярной системе координат.

Пусть на плоскости Оху одновременно введена и полярная система координат Orφ (рис. 2.9):

 Оp - полярная ось, которая совпадает с осью Ох; φ - полярный угол; r - полярный радиус точки М.

Тогда, как известно:

 Для полярной системы координатная сетка представляет собой пересечение окружностей увеличивающихся радиусов r с лучами, выходящими из точки О под возрастающими углами φ к полярной оси (рис. 2.10).

 Рассмотрим элементарный участок полярной сетки (рис. 2.11).

Тогда его площадь ΔS можно найти как разность площадей S₁ и S₂ полярных секторов радиусов r+Δr и r с раствором угла Δφ:

При Δr 0, Δφ 0 получаем ΔS≈ r·Δr·Δφ.

Таким образом, при замене переменных по формуле (2.12) дифференциал площади в полярной системе координат преобразуется так:

(Напомним, что в декартовой системе координат Оху прямоугольная сетка дает dS=dx·dy.)

Замечание.

Формулу (2.13) можно получить и по-другому, используя Якобиан J - "коэффициент искажения" площади при переходе к другой системе координат. А именно

  что совпадает с (2.13).

 

Теорема

Если область D - является правильной в полярной системе координат Оrφ, то двойной интеграл в этих координатах вычисляется так: