Уравнения второго порядка, допускающие пони­жение порядка.

Рассмотрим три случая, когда решение уравнения с помощью замены переменной водится к уравнению первого порядка. Такое преобразование уравнения называется понижением порядка.

1. Уравнение вида y'' = f (x).

Уравнение не содержит y и у'.

Введем новую функцию z(x), и поло­жим z(x) = y'.

Тогда z'(x) = y'', и уравнение превращается в уравнение первого порядка: z'(x) = f(x) с функцией z(x).

Решая его, находим: z(x) = 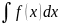+ C₁. Так как z(x) = y', то y' = 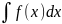+ C₁. Отсюда, интегрируя еще раз, получаем решение:

y = 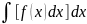+ C₁x + C₂

где C₁ и C₂ - произвольные постоянные.

Пример 1.

Найти общее решение уравнения y'' = x.

Решение:

Полагая z(x) = y', получаем уравнение первого порядка z'(x) = х. Интегрируя его, найдем

z(x) =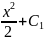 . Заменяя z(x) на y', интегрируя его еще раз, находим искомое общее решение:

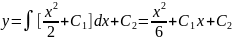
2. Уравнение вида y" = f (x,y').

Уравнение не содержит явным образом искомой функции y. Обозначим производную y' через z, т. е. положим z(x) = y`, тогда z`(x) = y``, и уравнение, преобразуемое в уравнение первого порядка относительно z(x): z`(x)=f(x,z).Решая его, найдем z(x)=φ(x, C<sub>1</sub>). Так как z(x) = y`,то y`= φ(x, C₁). Отсюда, интегрируя еще раз получаем искомое решение:

^y = ^.

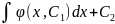где C₁ и C₂ - произвольные постоянные

Пример 2.

Найти общее решение уравнения y''-3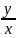 = x.

Решение: Полагая z(x) = y`,получаем линейное уравнение первого порядка

^z'-3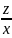 = x. Решая его, найдем z(x) =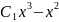 , тогда y`= и y=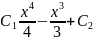 – искомое решение.

3. Уравнение вида y'' = f (y,y').

Уравнение не содержит явным образом независимой переменной x. Введем новую функцию z(у), полагая y`=z, Тогда

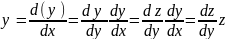
Подставляя в уравнение выражения y^' и y^'', получим уравнение первого порядка относительно вспомогательной функции z.

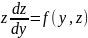
Решая его найдем φ(у, C₁). Так как 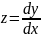, то

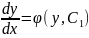
Отсюда 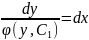Полученное уравнение с разделяющими переменными, из которых находим общее решение данного уравнения

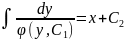
Лекция 11. Решение примеров.

Пример 3.

Найти общее решение уравнения yy``- 2y`²=0

Решение: Полагая у`= z(y) и учитывая что у``=z 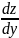получаем, 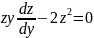. Это уравнение первого порядка с разделяющимися переменными. Приводя его к виду 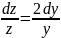и интегрируя, имеем

ln |z|=2 ln|y|+ln |C₁|, откуда z= C₁y².Учитывая, что z 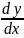, находим откуда получаем искомое решение 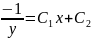или 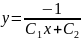. При сокращении на z было потеряно решение уравнения z=y``=0, т.е. у = С=const. В данном случае оно содержится в общем решении, так как получается из него при 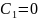, за исключением решения у=0.

Решение уравнений вида: у⁽ⁿ⁾=f(x).(6)

Это легко решается. Действительно, интегрируя последовательно n раз, получаем:

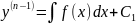
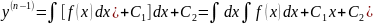
y=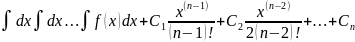 (7)

Где 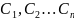- произвольные постоянные. Функция (7) является общим решением уравнения (6).

Пример 4.

Найти общее решение уравнения третьего порядка у```= e^x и вычислить его частное решение, удовлетворяющим начальным условиям: y=0, х=0, y`=0, х=0, y``=1, х=0.

Решение: Последовательно интегрируя, находим у``= e^x + C₁, у`= e^x + C₁х+ C_2. Интегрируя еще раз , получаем общее решение данного уравнения:

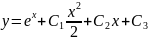, где - - произвольные постоянные.

Подставляя в выражение для y,y`,y`` начальные условия имеем 0=1+ C_3. 0=1+ C_2. 1=1+ C_1. Откуда находим C₁=0, C₂= -1, C₃= -1, Итак, 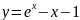искомое частное решение.