
- •Лекция 1.
- •Основные сведения о рядах.
- •Лекция 2. Признаки сходимости числовых рядов с положительными членами.
- •Лекция 3
- •Признак Коши
- •Знакопеременные ряды
- •Знакочередующиеся ряды
- •Признак Лейбница
- •Лекция 4 Теорема Абеля
- •Ряд Тейлора, ряд Маклорена
- •Лекция 5.
- •Лекция 6 Дифференциальные уравнения.
- •Лекция 8.
- •Дифференциальные уравнение приводящиеся к однородным.
- •Линейные дифференциальные уравнения первого порядка.
- •Лекция 9.
- •Дифференциальные уравнения второго порядка.
- •Лекция 10.
- •Уравнения второго порядка, допускающие понижение порядка.
- •Лекция 11. Решение примеров.
- •Линейные уравнения с постоянными коэффициентами.
- •Линейное однородное уравнение.
- •Лекция 12. Решение примеров:
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Лекция 13. Решение примеров:
- •3) Правая часть имеет вид:
- •4) Правая часть уравнения имеет вид:
- •Лекция 14.
- •Задача коши и кривая задача для уравнения второго порядка.
- •Использование дифференциальных уравнений в экономической динамике.
- •15 Лекция Решение примеров.
- •Интегрирование дифференциальных уравнений с помощью рядов.
Ряд Тейлора, ряд Маклорена
Если
функция f (x)
разлагается в степенной ряд f (x)=
с0+
с1(х-а)+с2(х-а)2+
с3(х-а)3+…+ск(х-а)к
+…
в некоторый окрестности точки а, т.е. в
интервале (а-h,a+h),
то коэффициенты этого ряда определяются
по формулам: с0=
F(a),
ск=
Следовательно,
f(x)=f(a)+
Ряд, сходящийся в правой части формулы называется рядом Тейлора для функции f(x)
Равенство
выполняется ряд Тейлора сходится к f(x)
в интервале (а-h,a+h),
если остаток ряда Тейлора rn(x)=
(f(x)-f(a)- стремиться к нулю при неограниченном
возрастании n:
стремиться к нулю при неограниченном
возрастании n: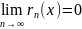 при всех х из интервала (а-h,a+h).
при всех х из интервала (а-h,a+h).
Формула (3) в частном случае при а=0 определяет разложение функции в ряд Маклорена:
f(x)=
f(0)+
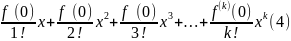
Лекция 5.
Рассмотрим разложение в ряд Маклорена элементарных функций.
Пусть f(x)=ex По формулам Тейлора:
![]() +
Rn(x)
,
+
Rn(x)
,
где
Rn(x)=![]()
Так
как при фиксированном х величина ex
ограничена (а значит, ограничены все
производные) то
 Следовательно, при всех
Следовательно, при всех
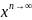
![]() + ….
+ ….
Аналогичным образом получаем разложение в ряд функций f(x)= sin x и f(x)= cos x (здесь также при всех х)
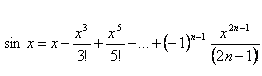 +
….
+
….
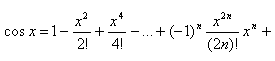 ….
….
Разложим в ряд Маклорена функцию f(x)= (1+x)m, где m- произвольное постоянное число.
Найдя f(0), f `(0), f (n)(0)… получим ряд (называемый биноминальным)
![]()
Определим радиус сходимости этого ряда
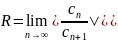 Так
как Cn=
Так
как Cn=
![]()
Cn+1= ,
то
,
то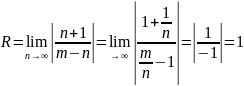
Таким образом биноминальный ряд сходится при Х ε (-1,1) и расходится при Х<-1 и Х>1. Сходится ли этот ряд при Х=1 и Х=-1, необходимо исследовать в каждом случае отдельно.
Осталось показать, что сумма этого ряда при Х ε (-1,1) действительно равна (1+x)m. Оценка остаточного члена в этом случае довольно сложна, поэтому доказательство опустим.
Итак , при Х ε (-1,1)
![]()
В частности при m= -1
 Интегрируя
это равенство от 0 до Х, где X<|1|,
получим:
Интегрируя
это равенство от 0 до Х, где X<|1|,
получим:
 Откуда
легко получить разложение функции:
Откуда
легко получить разложение функции:
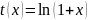
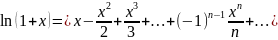 это
равенство справедливо в интервале
(-1,1). Можно показать, что оно справедливо
при Х=1
это
равенство справедливо в интервале
(-1,1). Можно показать, что оно справедливо
при Х=1
Положив в разложении х=t2 , после интегрирования получим разложение в ряд функции
F(x)= arctg x. Справедливо при X<|1|,
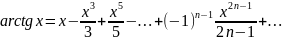 Это
верно при Х=1
Это
верно при Х=1
Пусть в формуле m= -1/2, n= -t2
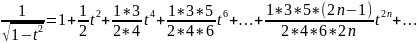
Интегрируя получаем, при Х ε (-1,1).

Геометрический ряд
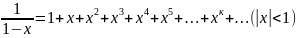
Найти:

Заменив
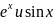 их разложениями в степенные ряды,
получаем
их разложениями в степенные ряды,
получаем

Найти:

Используем
разложение
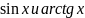 в степенные ряды, получаем:
в степенные ряды, получаем:
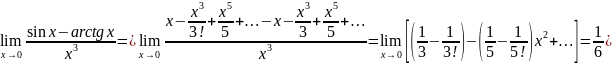
С помощью рядов Тейлора вычисляют значения так называемых не берущиеся интегралы .
Вычислить интеграл:
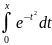 сначала
разложим подынтегральную функцию в
ряд, заменяя Х на –х2
в разложении функции ex
сначала
разложим подынтегральную функцию в
ряд, заменяя Х на –х2
в разложении функции ex
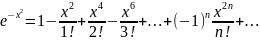 Интегрируя
равенство, получаем:
Интегрируя
равенство, получаем:
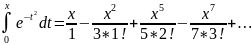 (1)
Таким
образом,
с помощью формулы (1) можно вычислить
значение данного интеграла для любого
Х с любой степенной точки.
(1)
Таким
образом,
с помощью формулы (1) можно вычислить
значение данного интеграла для любого
Х с любой степенной точки.
Лекция 6 Дифференциальные уравнения.
Основные понятия.
Дифференциальным уравнением называется уравнения вида F(x,y,y`,y``,…,y(n))=0, где х- независимая переменная, y=f(x) искомая функция. y,y`,y``,…,y(n) - ее производные.
Решением дифференциального уравнения называется функция y=f(x),которая при подстановке ее и ее производных обращает равенство F(x,y,y`,y``,…,y(n))=0 в тождество.
Порядком дифференциального уравнения называется наибольший порядок n входящей в него производной.
Примеры:
Решить дифференциальное уравнение:
y`+sin x=0
Запишем уравнение в виде y`= - sin x. По определению первообразной решением этого уравнения является первообразная для функции f(x)= - sin x.
Поэтому
решением данного уравнения имеют вид:
В общем виде для уравнения y`=f(x) решениями будут функции
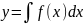 которые являются первообразными для
f(x).
которые являются первообразными для
f(x).
Интегрированием дифференциального уравнения называется процесс нахождения его решений.
Интегральной кривой называется график решения дифференциального уравнения.
Например:
для уравнения y`=
- sin
x
интегральные кривые являются графиками
функции
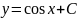 ,
полученным из графика
,
полученным из графика
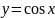 сдвигом вверх (вниз) на константу С.
сдвигом вверх (вниз) на константу С.
Общим решением дифференциального уравнения F(x,y,y`,y``,…,y(n))=0 порядка n называется такое решение y= f(x,C1, C2,… Cn,) которое является функцией от независимой переменной X от n произвольных независимых постоянных C1, C2,… Cn.
Частным решением называется решение, получаемое из общего решения, при некоторых конкретных значениях постоянных C1, C2,… Cn.
Пример:
Для уравнения второго порядка y`` =0 общее решение имеет вид y = C1х+ C2. Одним из частных решений будет решение y=x полученное при C1=1 ,C2=0.
Дифференциальные уравнения первого порядка.
Разрешенным относительно производной называется дифференциальное уравнение первого порядка F(x,y,y`)=0, которое можно записать в общем виде y`=f(x, y).
Уравнение с разделяющимися переменными.
Решением уравнения вида y`=f(x, y), сводящихся к нахождению неопределенных интегралов, если функция двух переменных f(x, y) представима в виде произведения двух функций одной переменной
f(x,
y)
=g(x)*h(y),
заменяя y`
на
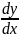 ,
получаем
,
получаем
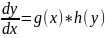
Уравнением
с разделяющимися переменными
называется уравнение вида
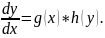 По-другому такие уравнения можно записать
в виде:
По-другому такие уравнения можно записать
в виде:
М(х) dx+N(y) dy=0
или
М(х) dx= - N(y) dy
Интегрируя
обе части последнего равенства,
получаем:

Общее решение Φ(x,y,C)=0 заданное в неявном виде, называется интегралом этого уравнения.
Геометрически общее решение (и общий интеграл) представляется собой семейство интегральных кривых на плоскости, зависящее от одного параметра Сю
Частным решением уравнения называется решение, полученное из общего решения при фиксированном значении С: y= φ(x,C0), где C0- число аналогично определяется частный интеграл Φ(x,y,C0)=0
Задача Коши.
Найдите решение y=f(x), дифференциального уравнения первого порядка, удовлетворявшее начальному условию y=y0 при x=x0. Другими словами, найти интегральную кривую этого уравнения , проходящую через точку М0 (x0, y0).
Лекция 7.
Примеры:
Пусть мы имеем уравнение

Функция y= sin x, y= 2cos x, y= 3sin x- cos x и вообще функция вида y= C1 sin x, y= C2 cos x, или
y= C1 sin x+ C2 cos x является решениями данного уравнения при любом выбор постоянных C1 и C2, в этом легко убедиться, подставив заданные функции в уравнение. Наряду с обыкновенными дифференциальными уравнениями.
Рассмотрим уравнение y`x-x2-y=0. Его решениями будут все функции вида: y= x2+Cx, где С- любое постоянное. Действительно, дифференцируя функцию y=x2+Cx ,находим y`=2х+С. Подставляя выражения y и y` в исходное уравнение, получаем тождество (2х+С) x-x2- Cx=0
Каждое из уравнений, рассмотренных в примерах 1 и 2, имеет бесчисленное множество решений.
Рассмотрим уравнение y` =
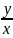
Разделяя
переменные, получаем:
 Интегрируя, имеем
Интегрируя, имеем
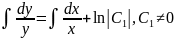 или
или
 Потенцируя, находим
Потенцируя, находим
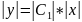 ,
что эквивалентно уравнению
,
что эквивалентно уравнению
 .
Полагая
.
Полагая
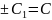 окончательно получаем
окончательно получаем


 Заметим,
что y=0
также решение уравнения (оно было
потеряно при делении на y).
Это решение можно включить в (9), если
считать что постоянная С принимает
значение С=0. Геометрическими общее
решение (9) представляет собой семейство
прямых проходящих через начало координат.
Пусть
требуется выделить из общего решения
(9) частное решение , удовлетворяющее
следующим начальным условиям: х0=1,
у0=2.
Подставляя эти значения в общее решение
вместо х и у, получаем 2=C•1, откуда С=2.
Таким образом , искомое частное решение
y =2x.
Заметим,
что y=0
также решение уравнения (оно было
потеряно при делении на y).
Это решение можно включить в (9), если
считать что постоянная С принимает
значение С=0. Геометрическими общее
решение (9) представляет собой семейство
прямых проходящих через начало координат.
Пусть
требуется выделить из общего решения
(9) частное решение , удовлетворяющее
следующим начальным условиям: х0=1,
у0=2.
Подставляя эти значения в общее решение
вместо х и у, получаем 2=C•1, откуда С=2.
Таким образом , искомое частное решение
y =2x.
Для уравнения первого порядка
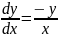 общим уравнением будет семейство
функций
общим уравнением будет семейство
функций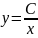 - это можно проверить простой подстановкой
в уравнение. Найдем
честное решение, удовлетворяющее
следующему начальному условию:
х0=2,
у0=1.
Подставляя
эти значения :
х0,
у0
в формулу
,получаем
- это можно проверить простой подстановкой
в уравнение. Найдем
честное решение, удовлетворяющее
следующему начальному условию:
х0=2,
у0=1.
Подставляя
эти значения :
х0,
у0
в формулу
,получаем
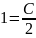 или С=2. Следовательно, искомым частным
решением будет функция
или С=2. Следовательно, искомым частным
решением будет функция
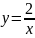
Рис.1
Дано семейство парабол:
Рис.2
Найдите
дифференциальное уравнение семейства
парабол y=Cx2.
Дифференцируя по х уравнение семейства,
найдем
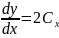 . Подставляя сюда значение найдем:
. Подставляя сюда значение найдем:
 из уравнения семейства получаем
дифференциальное уравнение данного
семейства,
из уравнения семейства получаем
дифференциальное уравнение данного
семейства,
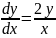 Это дифференциальное уравнение имеет
смысл при х≠0, т.е.в точке любой области,
не содержащей точек на оси Оy/
Это дифференциальное уравнение имеет
смысл при х≠0, т.е.в точке любой области,
не содержащей точек на оси Оy/
