1)Дифференцирование функций заданных параметрически

  До сих пор функция записывалась в явном виде y=f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в параметрической форме в виде двух уравнений

где t - вспомогательная переменная, называемая параметром.   Заметим, что функция может быть представлена в параметрической форме различными способами.   Например, функция, записанная в неявном виде x² + y² = 1 может быть представлена в явном виде:   и в параметрической форме:

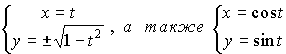
  Заметим, что x² + y² = 1 есть уравнение окружности единичного радиуса с центром в начале координат.   В первом параметрическом представлении уравнения x² + y² = 1 параметр t изменяется от -1 до +1 и равен абциссе подвижной точки окружности, во втором случае параметр t изменяется от 0 до 2П и равен углу, образованному радиусом подвижной точки и осью Ox.   Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме

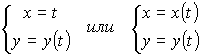
От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=(y), так как уравнение F(x,y)=0 может оказаться неразрешимым относительно y или x .   Лего перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найти t=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)

y=y[t(x)]=f(x)

   От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно.    Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения

и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0.    Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если

y(t)=f [ x(t) ].

   Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как функцию от x. То есть t=t(x). Тогда y=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле

и применим формулу, связывающую производные обратных функций:

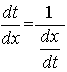
   Введя обозначения

,       

получим

Теперь найдем вторую производную от функции, заданной в параметрической форме.    Из предыдущего уравнения и определения второй производной следует, что

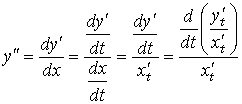
   но

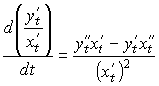
   Следовательно

   где

              

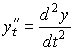
2) Теорема Ролля

   Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0.    Доказательство. Так как функция f(x) непрерывна на [a, b],то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m.    Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана.    Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.

Геометрический смысл теоремы Ролля

   Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах f(a) = f(b) равные значения, существует точка (c; f(c)), в которой касательная параллельна оси Оx.

3) Теорема Лагранжа.  Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f(b) - f(a) = (b - a)f '(x).

  Доказательство. Рассмотрим вспомогательную функцию

F(x) = f(x) - k(x - a),

где   - угловой коэффициент хорды AB (смотри рисунок 2).   Эта функция удовлетворяет всем условиям теоремы Ролля.   В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем

  Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b).   Следовательно, по теореме Ролля, в интервале (a, b) найдется такая точка x₀, что

F'(x₀) = 0,

т.е.

f ' (x₀) - k = 0

или

  Отсюда имеем

f(b) - f(a) = (b - a)f ' (x₀),

что и требовалось доказать.   Так как a + (b - a) = b, то величина a + Q(b - a), где Q - правильная положительная дробь (0 < Q < 1), равна какому-то числу в интервале (a, b), поэтому формулу Лагранжа можно записать в виде

f(b) - f(a) = (b - a)f ' [a + Q(b - a)]

  Если положить a = x, b = x + Dx, откуда b - a = Dx, то формула Лагранжа запишется в виде

Dy = f(x + Dx) - f(x) = Dxf ' (x + QDx).

  Ранее было доказано, что если функция равна постоянной C при любом значении x в интервале (a, b), то ее производная равна нулю.   Докажем теперь обратную теорему, являющуюся следствием теоремы Лагранжа:   Если произвоодная f ' (x) обращается в нуль для любых значений x в интервале (a, b), то в этом интервале f(x) = C.   В самом деле, если x₁ и x₂ - два любых значения в интервале (a, b), то в силу теоремы Лагранжа, имеем

f(x₂) - f(x₁) = (x₂ - x₁)f'(x₀),

где, x₁ < x₀ < x₂. Но так как f'(x₀) = 0, то

f(x₂) - f(x₁) = 0,

что и доказывает нашу теорему.    Отсюда непосредственно вытекает важная теорема:    Если две функции f₁ (x) и f₂ (x) имеют одну и ту же производную в интервале (a, b), то они на данном интервале отличаются друг от друга на постоянную величину.    В самом деле, рассмотрим функцию

j(x) = f₂(x) - f₁(x).

   Тогда для любого значения x из интервала (a, b)

j'(x) = f₂'(x) - f₁'(x) = 0.

   Но это означает, что j(x) = C и, следовательно

f₂(x) - f₁(x) = С.

4) Теорема Коши́ о среднем значении является обобщением теоремы Лагранжа о конечных приращениях.

Формулировка 

Пусть на отрезке определены две непрерывные функции  . Пусть также  существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть  , и   Тогда

.

Cледствие 

Полагая  , получаем теорему Лагранжа о конечных приращениях.

5) Формулы и ряды Тейлора и Маклорена.  Разложение функций в степенные ряды.

 Если функция  y = f(x)  имеет производные в окрестности точки x = x₀   до (n+1) - го порядка включительно, то существует точка      , такая, что  

(1)

где        

Формула (1) называется формулой Тейлора функции y = f(x)  для точки x₀,

R_n (x) - остаточным членом формулы Тейлора в форме Лагранжа. 

Многочлен 

называется многочленом Тейлора функции y = f(x).

При x₀ = 0  приходим к частному случаю формулы (1): 

(2)

где 

Формула (2) называется формулой Маклорена функции   y = f(x). 

Сформулируем условие разложимости функции в ряд Тейлора.

Если функция  f(x)  дифференцируема в окрестности точки x₀ любое число раз и в некоторой окрестности этой точки      , то 

(3)

 При x₀ = 0  

(4)

Ряд (3) называется рядом Тейлора, а ряд (4) – рядом Маклорена.

Приведем разложения в степенные ряды некоторых функций:

	(5)
	(6)
	(7)
	(8)
(-1 < x < 1)	(9)

Для каждого случая в скобках указана область, в которой степенной ряд сходится к соответствующей функции. 

Последний ряд, называемый биномиальным, на концах интервала сходимости ведет себя по - разному в зависимости от  ; при   абсолютно сходится в   ; при   -1 < m < 0расходится в точке x = -1 и условно сходится в точке x = 1 при   расходится в точках  . 

В общем случае разложение в степенные ряды основано на использовании рядов Тейлора или Маклорена. Но на практике степенные ряды многих функций можно найти формально, используя ряды (5 - 9).

Например, при разложении в степенной ряд функции   в формулу (6) вместо подставляем   . Тогда:   

Полученный ряд сходится при любых   , но следует помнить, что функция   не определена при x < 0 . Поэтому найденный ряд сходится к функции только в полуинтервале   .

Аналогично можно записать степенные ряды функций  f (x) = e^-2x   и   . 

  

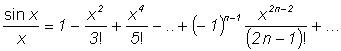
5)Возрастание и убывание функции на интервале, экстремумы.

Очень важную информацию о поведении функции предоставляют промежутки возрастания и убывания. Их нахождение является частью процесса исследования функции и построения графика. К тому же точкам экстремума, в которых происходит смена с возрастания на убывание или с убывания на возрастание, уделяется особое внимание при нахождении наибольшего и наименьшего значения функции на некотором интервале. В этой статье дадим необходимые определения, сформулируем достаточный признак возрастания и убывания функции на интервале и достаточные условия существования экстремума, применим всю эту теорию к решению примеров и задач. Рекомендуем при необходимости обращаться к разделу дифференцирование функции, так как все признаки в этой статье основаны на нахождении производной. 

Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X. К примеру, из свойств основных элементарных функций мы знаем, что y = sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале 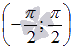  мы можем утверждать о возрастании на отрезке  . Точку   называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке максимума называют максимумом функции и обозначают  . Точку   называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке минимума называют минимумом функции и обозначают  . Под окрестностью точки   понимают интервал  , где   - достаточно малое положительное число.  Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

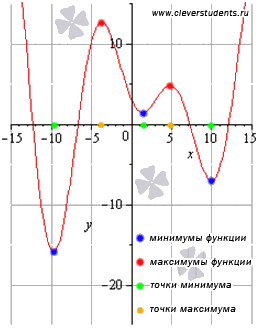
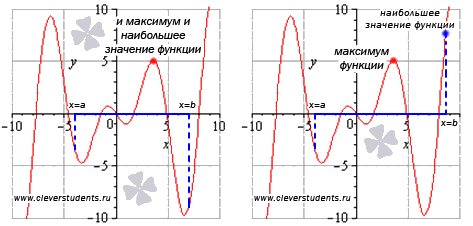
Не путайте экстремумы функции с наибольшим и наименьшим значением функции. На первом рисунке наибольшее значение функции на отрезке [a; b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x = b, которая не является точкой максимума.

Достаточные признаки возрастания и убывания функции.

На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:

если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

найти область определения функции;

найти производную функции;

решить неравенства   и   на области определения; к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

6) Точки экстремума

   Точка x₀ называется точкой строгого локального максимума (минимума) функции f (x), если для всех значений аргумента из некоторой достаточно малой δ(дельта) - окрестности точки х₀ выполняется неравенство

f (x) < f (x₀) ( f ( x) > f ( x₀ ) )

при х ≠ x₀.    Локальный максимум и локальный минимум объединяются общим названием экстремум. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство f (x) < f ( x₀) ( f (x) > f ( x₀ )) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x₀.     Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то другого локального минимума.    В точках экстремума приращение функции имеет определённый знак. Если Δ f = f ( x₀ + h ) − f ( x₀) ≥ 0 для достаточно малых значений h, то точка х₀ является точкой локального минимума. Если Δ f = f( x₀ + h ) − f (x₀) ≤ 0 для достаточно малых значений h, то точка х₀ является точкой локального максимума. Точки экстремума это точки графика функции, которые отделяют участки определённой монотонности друг от друга.    Ниже приведены виды точек экстремумов. В первых двух функция определена и производная существует, такие точки называются стационарными.     Функция в точках экстремума определена, однако производной в точке экстремума может не существовать.

Необходимое условие экстремума

   Теорема.

 Если х₀ — точка экстремума функции f (x), то либо в этой точке производная обращается в нуль f ' (x₀) = 0 (в стационарных точках), либо в этих точках производная не существует (в угловых точках).    Доказательство. Рассмотрим разложение функции в окрестности точки х₀ в ряд Тейлора с остаточным членом в форме Пеано

Δ f (x) = f ' (x₀)·Δ x + o(Δ x).

Так как остаточный член является бесконечно малой величиной относительно приращения аргумента, то

sign Δ f (x) = sign f ' (x₀)·sign Δ x,

и знак приращения функции зависит от знака приращения аргумента sign (Δ x). Что недопустимо для точек экстремума. Следовательно производная функции в точке х₀ или равна нулю, или не должна существовать.

Достаточное условие экстремума

   Теорема. 

Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х₁, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х₁. Если при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то при х = х₁ функция имеет локальный максимум. Если же при переходе слева направо через эту точку х₁производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.    Комментарий. Если в достаточно малой окрестности точки х₁ справедливо f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁, то в точке х₁ функция имеет максимум; если f ' (x) < 0 при х < x₁, f ' (x) > 0 при х >x₁, то в точке х₁ функция имеет минимум.    Доказательство. Пусть при переходе слева направо через эту точку х₁ производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х₁, имеем f ' (x) > 0 при х < x₁, f ' (x) < 0 при х > x₁. Применяя теорему Лагранжа к разности f (x) − f ( x₁), получим

f ( x ) − f ( x₁ ) = f ' ( c )·( x − x₁ ).

где с лежит между точками х и х₁. По условию теоремы

sign f ' ( c ) = − sign ( x − x₁ ),

поэтому в произвольно малой окрестности точки х₁ имеем

f ( x ) < f ( x₁ ).

В этом случае точка х₁ есть точка локального максимума, что и требовалось доказать.

Исследование поведения функций в точке х₀ с помощью производных высшего порядка

   Теорема. 

Пусть функция f ( x ) определена в некоторой ε – окрестности точки х₀, причём f ' ( x₀ ) = f '' ( x₀) = … = f ^{( k - 1 )} = 0  и f ^(k) ( x₀ ) ≠ 0. Тогда точка х₀ является точкой локального максимума, если k – чётное и f ^(k) ( x₀ ) < 0, и точкой локального минимума, если k – чётное и f ^(k) ( x₀ ) > 0. Если k – нечётное, то критическая точка х₀ не является точкой экстремума; является точкой возрастания функции f ( x ) в случае f ^(k) ( x₀ ) > 0 и является точкой убывания функции f ( x ) в случае f ^(k) ( x₀ ) < 0.    Доказательство. Воспользуемся формулой Тейлора для функции f ( x ) в точке х₀:

.

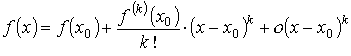Поэтому

.

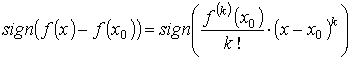Если k – чётное, то

sign ( f ( x ) − f ( x₀ ) ) = sign ( f ^(k)( x₀ ) ),

из чего следует вывод относительно экстремума функции в условиях этой теоремы. Если k – нечётное, то

sign (f ( x ) − f ( x₀ )) = sign ( f ^(k)( x₀ ) )·sign ( x − x₀ ),

и приращение функции зависит от знака приращения аргумента с поправкой на знак величины f ^(k) ( x₀ ), из чего следует вывод относительно точки монотонности функции в условиях этой теоремы.

7) Вторая производная. 

Если производная  f ' ( x ) функции  f ( x ) дифференцируема в точке ( x₀ ), то её производная называется второй производной функции  f ( x )  в точке ( x₀ ), и обозначается  f '' (x₀ ).  

 

Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

 

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x   ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x   ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

П р и м е р .

Рассмотрим график функции  y = x3 : Эта функция является вогнутой при  x > 0  и выпуклой при  x < 0. В самом деле,  y'' = 6x, но 6x > 0 при  x > 0  и  6x < 0  при  x < 0, следовательно,  y'' > 0 при x > 0 и  y'' < 0 при x < 0,откуда следует, что функция  y = x3 является вогнутой при  x > 0 и выпуклой при x < 0. Тогда  x = 0 является точкой перегиба функции  y = x3.

9) Определение точки перегиба

   Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба.     В окрестности такой точки x ₀ график функции y = f (x) слева и справа от точки x₀ имеет разные направления выпуклости.    Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой - над нею.     В окрестности точки перегиба график функции геометрически переходит с одной сторон касательной на другую и "перегибается" через нее. Отсюда и произошло название "точка перегиба".

Необходимое условие точки перегиба

   Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x₀, f(x₀)) была точкой перегиба графика функции y = f (x) необходимо, чтобыf " (x₀) = 0.     Доказательство. Предположим обратное, пусть f "(x₀) ≠ 0. Тогда в силу непрерывности второй производной по теореме об устойчивости знака непрерывной функции существует окрестность точки x₀, в которой f ″(x) < 0 (f "(x) > 0), и, значит график функции y = f (x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке M(x₀; f (x₀ )). Полученное противоречие доказывает теорему.    Не всякая точка М (x₀, f (x₀)), для которой f " (x₀) = 0, является точкой перегиба. Например, график функции y = f(x) = x⁴ не имеет перегиба в точке (0; 0), хотя f " (х) = 12·x ² = 0 при х = 0. Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки М (x₀; f (x₀)) графика, для которых f "(x₀) = 0, будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует сформулировать достаточное условие перегиба.

Достаточное условие точки перегиба

   Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x₀ интервала (a, b), за исключением, быть может самой точки х₀, а график функции имеет касательную в точке С = (х₀, f (x₀)). Если при переходе через точку х₀ вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).    Доказательство. Из того, что f "(x₀) слева и справа от точки x₀ имеет разные знаки, то направление выпуклости графика функции слева и справа от точки x₀ является различным. Это и означает наличие перегиба в точке M(x₀; f (x₀)).

10) Экстремумы функции

Определение 1. Говорят, что в точке  функция  имеет локальный максимум (локальный минимум), если  .

В этом определении обратите внимание на слово “локальный”. Оно означает, что  принимает свое наибольшее значение в точке   только по отношению к отрезку  . Вне этого отрезка о поведении функции ничего не утверждается: она может принять там и значение, большее чем  . То же самое можно сказать и по отн. к локальному минимуму.

Определение 2.Говорят, что функция   имеет в точке  глобальный максимум (минимум) на множестве   если  .

Термины “максимум” и “минимум” объединяют одним словом “экстремум” и говорят о локальном или глобальном экстремуме. Отметьте еще, что для непрерывной функции локальный максимумы или минимумы чередуются.

Нахождение локальных экстремумов - одна из важнейших задач исследования функций имеющая большое практическое значение. Перейдем к е изучению.

Пусть функция  FO определена на некотором отрезке  . Научимся сначала находить локальные экстремумы, расположенные внутри этого отрезка.

Необходимое условие экстремума

Пусть в точке  , такой, что  , функция   принимает свое экстремальное, т.е. наибольшее или наименьшее значение. Тогда по теореме Ферма

Это и дает необходимое условие экстремума. Отметьте, что если выполнено условие  то это еще не означает, что в точке  функция имеет локальный экстремум. Условие   дает лишь точку “подозрительную” на экстремум, и что там на самом деле, - еще предстоит ответить.

Итак, пусть в некоторой точке выполняется условие Достаточное условие экстремума  , т.е. эта точка является “подозрительной” на экстремум. Что же на самом деле в этой точке?

Для дальнейшего основным для нас будет разложение функции в ряд Тейлора с остаточным членом в форме Пеано

*

и тот факт, что из-за условия   второе слагаемое в этом разложении исчезает.

Разберем основные случаи в порядке их усложнения.

А. Пусть  . тогда разложение (*) принимает вид

Функция   - это парабола. График   в окрестности точки   в зависимости от знака   изображен на рисунках

Из рисунков видно, что если  < то в точке   - локальный минимум, а если  , то в   - локальный максимум. Б. Пусть   но  . Тогда разложение (*) примет вид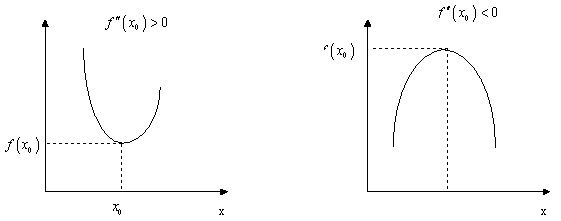

 

 

 

 

 

 

 

 

График функции   в окрестности точке   имеет вид

 

Отсюда видно, что экстремума в точке   нет.

В. Пусть   но

. Тогда

График функции   напоминает параболу. Поэтому график   в окрестности точки   имеет вид

Отсюда видно, что если   то в точке   - локальный минимум, а если , то в точке  - локальный максимум.

Г. Пусть   но . тогда   Так как  - нечетное число, то график   напоминает график функции  . Поэтому график   в окрестности точки   имеет вид

Отсюда видно, что в точке  экстремума нет.

 Случай, когда в точке   существуют лишь односторонние производные

На теорему Ферма можно ссылаться лишь тогда, когда в точке . Если же   не существует, то теорема Ферма не работает. Рассмотрим случай, когда в точке   существуют лишь односторонние производные   и . Вспомним, что производная - это тангенс угла наклона касательной к оси OY, будем иметь следующие четыре варианта

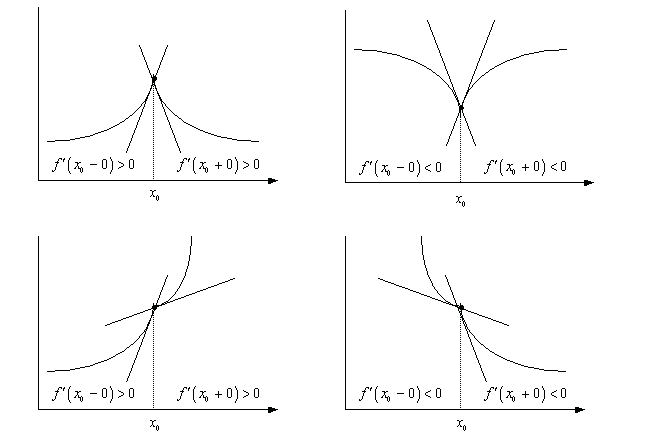
Отсюда видно, что если   и   имеют разные знаки, то в точке   - локальный экстремум. Если   и   имеют одинаковые знаки, то локального экстремума нет.

 Граничные точки

Рассмотрим наконец, граничные точки a и b отрезка  . Здесь поведение функции  может быть следующим.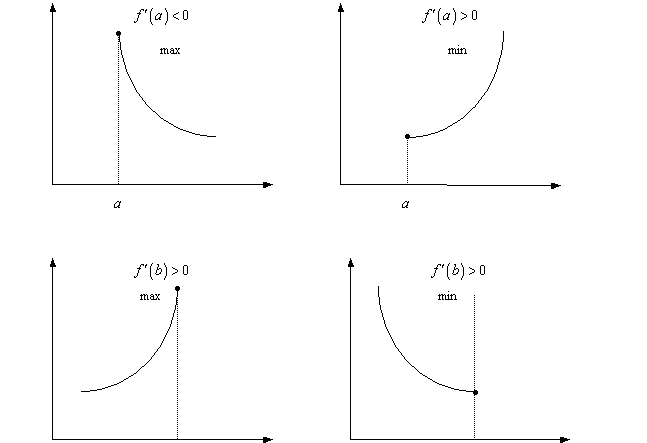

Таким образом, что мы имеем в граничных точках, определяется знаком первой производной.

Подведем итоги.

 Схема исследования функции на экстремумы

Чтобы исследовать экстремумы функции  надо сделать следующее:

1. Найти те точки  , в которых  . Это будут точки, “подозрительные” на наличие в них экстремума.

2. В точках где   найти первую по порядку старшинства производную, отличную от нуля. Если это будет производная четного порядка - в точке   локальный экстремум (если эта производная отрицательная - то максимум, если положительная - то минимум), если же нечетного порядка - в точке   экстремума нет.

3. Найти те точки, где существуют лишь односторонние производные. Если эти производные разных знаков - в точке локальный экстремум, если одного знака - экстремума нет.

4. Найти производные на границах области задания функции и определить, как ведет себя функция на границе.

5. Вычислить значения функции в точках локальных минимумов и максимумов и найти глобальный минимум (наименьший из локальных минимумов) и глобальный максимум (наибольший из локальных максимумов).

11) Асимптоты графика функции

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции  называется вертикальная прямая  , если   или  при каком-либо из условий:  ,  ,  . Заметим, что мы при этом не требуем, чтобы точка   принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:   или  , где  .     

        Пример 7.1   Рассмотрим функцию 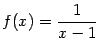 . График   имеет вертикальную асимптоту  , поскольку при   выполняется условие  , а также при   выполняется условие  .     

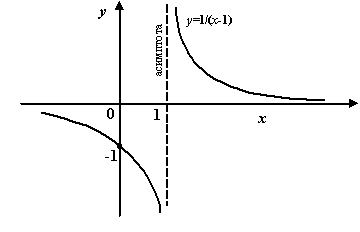
Рис.7.1.Вертикальная асимптота функции 

        Пример 7.2   Рассмотрим функцию  . Её график имеет вертикальную асимптоту  , так как   при  . То, что при   функция   не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая   являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать,   при  .)     

Рис.7.2.Вертикальная асимптота функции 

        Пример 7.3   Рассмотрим функцию 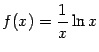 . Прямая   является вертикальной асимптотой графика  , так как   при  . Заметим, что слева от точки   функция вообще не определена.     

Рис.7.3.Вертикальная асимптота функции 

        Пример 7.4   График функци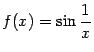и   не имеет при  вертикальной асимптоты, так как   -- ограниченная (числом 1) и, следовательно, локально ограниченная при   и не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция 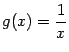  -- имеет вертикальную асимптоту  .     

Рис.7.4.График функции   не имеет вертикальной асимптоты

        Пример 7.5   Прямая   не является вертикальной асимптотой графика функции 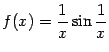 , поскольку здесь нельзя утверждать, что при  или   функция стремится к бесконечности. При некоторых малых значениях   значения   могут быть как угодно велики, однако при других малых   функция обращается в 0: так, при   (  ) значения функции равны   и стремятся к бесконечности при  , а при всех   вида   (  ) значения функции равны 0. В то же время как те, так и другие точки   при увеличении   попадают всё ближе и ближе к точке 0. Значит, функция   не является бесконечно большой при  , и прямая   -- не асимптота.     

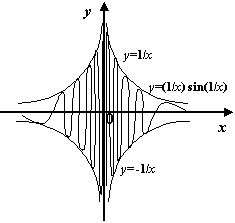
Рис.7.5.График функции   не имеет вертикальной асимптоты

Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.

12) Общая схема исследования функции и построения её графика

После того как мы обсудили многие аспекты поведения функции и способы их исследования, сформулируем общую схему исследования функции. Эта схема даст нам практический способ построения графика функции, отражающего основные черты её поведения.

Пусть дана функция  . Для её исследования нужно:

1). Найти её область определения  . Если это не слишком сложно, то полезно найти также область значений  . (Однако, во многих случаях, вопрос нахождения   откладывается до нахождения экстремумов функции.)

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси  ), не является ли она периодической.

3). Выяснить, как ведёт себя функция при приближении аргумента   к граничным точкам области определения  , если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции. Поясним сказанное примером:

        Пример 7.36   Пусть 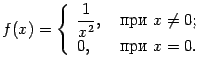  Эта функция определена на всей числовой оси, однако 0 является точкой разрыва функции: при   функция стремится к  . Значит, вертикальная прямая   служит вертикальной асимптотой функции, хотя функция и определена в точке  .     

4). Если область определения   вклоючает в себя лучи вида   или  , то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при   или   соответственно.

5). Найти точку пересечения графика с осью   (если  ). Для этого нужно вычислить значение  . Найти также точки пересечения графика с осью  , для чего найти корни уравнения   (или убедиться в отсутствии корней). Уравнение   часто удаётся решить лишь приближённо, но уже отделение корней¹⁹ помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

6). Найти интервалы монотонности функции   (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной  .

На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

7). Найти интервалы выпуклости и вогнутости функции. Это делается с помощью исследования знака второй производной  . Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.

8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график.

13.

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) даннойфункции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция   является первообразной  . Так как производнаяконстанты равна нулю,   будет иметь бесконечное количество первообразных; таких как   или   … и т. д.; таким образом семейство первообразных функции  можно обозначить как  , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

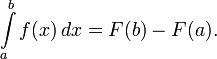
Это соотношение называется формулой Ньютона — Лейбница.

Неопределённый интегра́л для функции   — это совокупность всех первообразных данной функции.

Если функция   определена и непрерывна на промежутке   и   — её первообразная, то есть   при  , то

  ,

где С — произвольная постоянная.

Связь интегрирования и дифференцирования

теорема Барроу

Грубо говоря если после знака стоит например cosx,значит до этого выражение было sinx+с

Т.е. после знака интеграла в общем стоит то выражение,которое мы получаем после нахождения производной какого-то выражения

14.Свойства неопределенных интегралов

Свойства неопределенных интегралов

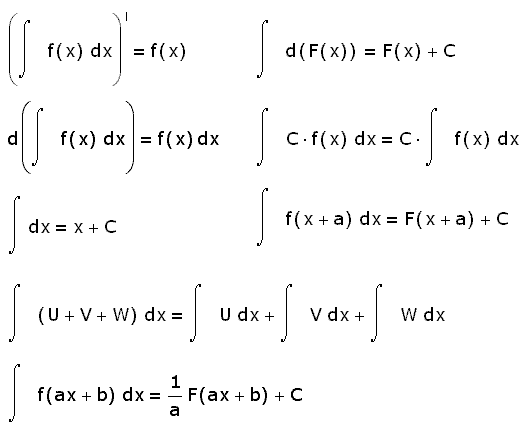
15

15.Комплексные числа

Ко́мпле́ксные^[1] чи́сла (устар. Мнимые числа^[2]), — расширение множества вещественных чисел, обычно обозначается  . Любое комплексное число может быть представлено как формальная сумма  , где   и   — вещественные числа,   — мнимая единица^[3].

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа  , 

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:   – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел   и  , если  , 

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная:  . Для наглядности ответ можно переписать так:  .

Рассчитаем вторую разность: Здесь действительная часть тоже составная: 

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью:  . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел   , 

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что   и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что 

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:  .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа  ,  . Найти частное  .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу   и смотрим на нашзнаменатель:  . В знаменателе уже есть  , поэтому сопряженным выражением в данном случае является  , то есть 

Согласно правилу, знаменатель нужно умножить на  , и, чтобы ничего не изменилось, домножить числитель на то же самое число  :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой   (помним, что  и не путаемся в знаках!!!).

Распишу подробно:

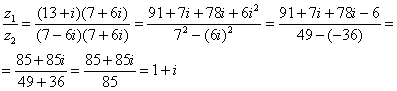
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде  .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел:  . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы:  . Для любителей порешать приведу правильный ответ: 

Редко, но встречается такое задание:

Пример 5

Дано комплексное число  . Записать данное число в алгебраической форме (т.е. в форме  ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу  . В знаменателе уже есть  , поэтому знаменатель и числитель нужно домножить на сопряженное выражение  , то есть на  :