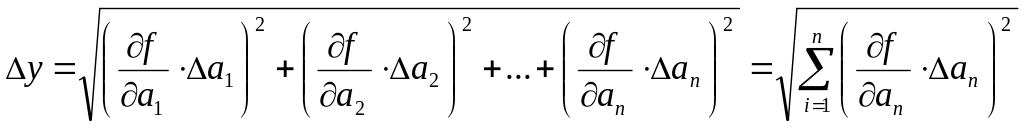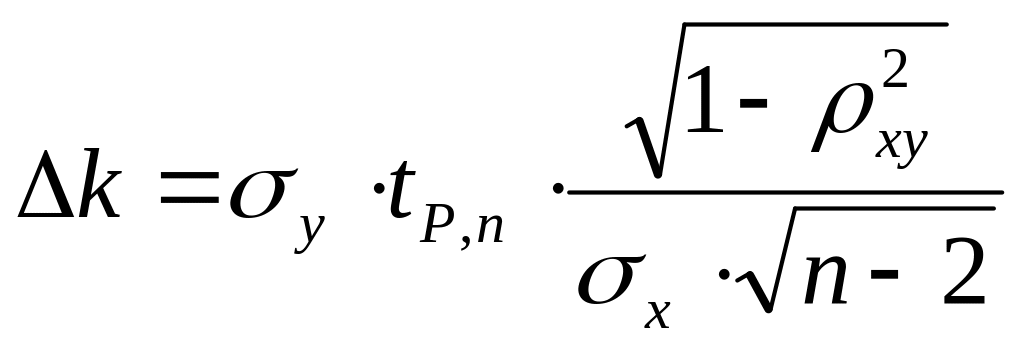1.1.3 Обробка результатів непрямих (посередніх) вимірювань.

При непрямих вимірюваннях фізичної величини спочатку проводяться прямі вимірювання фізичних величин , , …, (і обробляються, як у прикладі 1), а потім використовується формула для розрахунку результату непрямих вимірювань . Припустимо величина може бути виражена через , , …, як

.

(1.1.3.1)

Тоді для розрахунку потрібно підставити у цю формулу середні арифметичні значення , , …, :

(1.1.3.2)

Похибку непрямих вимірювань можна розрахувати по загальній диференційній формулі:

(1.1.3.3)

Відносну похибку непрямих вимірювань можна розрахувати по формулі:

(1.1.3.4)

Таким чином, якщо формула для розрахунків (функція ) має вигляд добутку, степеня, дробу, кореня, то зручніше розраховувати відносну похибку.

Приклад 2. Розрахувати об’єм циліндру і похибку його вимірювання, за умови що його діаметр рівний (12,2 мм ±0,2) мм; P=0,95; висота h рівна (24,5 ± 0,2) мм; Р=0,95.

1. Розрахуємо об’єм циліндра, підставивши результати прямих вимірювань в відому формулу для розрахунку об’єму циліндра:

мм3

2. Розрахуємо часткові похідні функції для обчислення , підставивши в формули значення висоти циліндра і його діаметру:

	мм2
	мм2

3. Розрахуємо похибку визначення об’єму циліндра:

мм3

4. Запишемо результат обчислень у вигляді мм³; Р=0,95.

В прикладі 2 формула для розрахунку досить проста, тому розрахунок похибки не дуже складний. Однак, для порівняння, при розрахунку відносної похибки замість п. 2 - 4 потрібно зробити:

2. Визначимо :

3. Розрахуємо часткові похідні і їх значення

	мм-1
	мм-1

4. Розрахуємо відносну похибку :

5. Знайдемо :

мм3

6. Запишемо результат обчислень у вигляді мм³; Р=0,95.

Як видно, в другому випадку обчислення простіші і, за умови що формула для розрахунку фізичної величини непрямим методом логарифмується, розрахунок відносної похибки є простішим для складніших формул розрахунку.

1.1.4 Метод найменших квадратів

Одним із завдань лабораторних робіт є дослідження взаємозв’язку між фізичними величинами. Припустимо, що вимірюються фізичні величини і і нам відома формула, яка пов’язує ці величини. Використовуючи дану формулу ми можемо лінеарізувати залежність і , тобто побудувати її на графіку таким чином, щоб експериментальні точки були близькі до прямої (конкретні способи лінеаризації будуть розглянуті в відповідних лабораторних роботах). Якщо, як було припущено вище, в наших вимірюваннях домінує випадкова похибка, то виміряна експериментальна точка може з однаковою ймовірністю опинитися вище чи нижче від очікуваного теоретичного значення. Маючи графік з експериментальними точками потрібно провести пряму так, щоб відстань від неї до експериментальних точок була мінімальною, або, іншими словами, кількість точок, що лежать над прямою, повинна бути рівній кількості точок під прямою. Наприклад, якщо ми досліджуємо закон Ома , і виміряли струм через опір та відповідну цьому струму напругу на опорі , то побудова залежності підтвердить справедливість закону Ома і дозволить обчислити значення самого опору . Якщо, як припущено вище, розподіл похибок нормальний, то отримати пряму можна мінімізуючи відстань від неї до експериментальних точок, як це робиться в методі найменших квадратів. В противному разі потрібно використовувати інші нелінійні методи.

Розглянемо метод найменших квадратів. Припустимо, що між величинами і існує лінійна залежність, тобто

.

(1.1.4.1)

В нашому розпорядженні є результати n вимірювань . Необхідно визначити коефіцієнти і , так щоб набувала мінімального значення величина

,

(1.1.4.2)

яка залежить від кута нахилу прямої і параметру . Заради зручності наступних викладок перейдемо від величини до . Згідно формул математичної статистики обидві ці величини матимуть екстремум за однакових умов. Таким чином

(1.1.4.3)

Цю рівність можна переписати у вигляді

,

(1.1.4.4)

Далі

(1.1.4.5)

де . Необхідні умови для мінімуму дають

	,	(1.1.4.6)
	.	(1.1.4.7)

Розв’язання цих рівнянь дасть

	,	(1.1.4.8)
		(1.1.4.9)

де .

Як можна показати, похибку визначення і можна розрахувати за формулами

		(1.1.4.10)
		(1.1.4.11)

Приклад 3. Розглянемо застосування методу найменших квадратів на практиці. Припустимо, що ми провели експеримент і отримали наступні результати вимірювань : (1,00; 5,00). (2,00; 5,43), (3,00; 6,25), (4,00; 6,70), (5,00; 7,05), (6,00; 7,80), (7,00; 8,30), (8,00; 8,80), (9,00; 9,50), (10,00; 9,80). Тут - фізична величина, значення якої ми задавали в ході експерименту, - фізична величина, яку ми вимірювали і яка відповідає , кількість вимірів .

1. Заносимо результати вимірювань у таблицю і розраховуємо суму і :

	1,00	5,00
	2,00	5,43
	3,00	6,25
	4,00	6,70
	5,00	7,05
	6,00	7,80
	7,00	8,30
	8,00	8,80
	9,00	9,50
	10,00	9,80
сума	55,00	74,63

2. Використовуючи табличні дані, розраховуємо і :

3. Заповнюємо всі стовпчики в таблиці:

	1,00	5,00	-4,500	-2,463	20,250	6,066	11,084
	2,00	5,43	-3,500	-2,033	12,250	4,133	7,116
	3,00	6,25	-2,500	-1,213	6,250	1,471	3,033
	4,00	6,70	-1,500	-0,763	2,250	0,582	1,145
	5,00	7,05	-0,500	-0,413	0,250	0,171	0,207
	6,00	7,80	0,500	0,337	0,250	0,114	0,169
	7,00	8,30	1,500	0,837	2,250	0,701	1,256
	8,00	8,80	2,500	1,337	6,250	1,788	3,343
	9,00	9,50	3,500	2,037	12,250	4,149	7,130
	10,00	9,80	4,500	2,337	20,250	5,462	10,517
сума	55,00	74,63			82,500	24,636	44,995

4. Розраховуємо і :

5. Розраховуємо і :

6. Розрахуємо , :

7. Розраховуємо , :

8. Запишемо результат згідно правил округлення:

	,
	,