2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
Приступим теперь к изучению методов интегрирования. Первый метод – метод непосредственного интегрирования основывается на таблице интегралов, свойствах интегралов и следующей теореме.
Об инвариантности формул интегрирования. Каждая формула интегрирования сохраняет свой вид, если в нее вместо независимой переменной подставить любую дифференцируемую функцию этой переменной. То есть, если
,
то
,
где
– дифференцируемая функция переменной
x.
Рассмотрим такие примеры.
Пример:
Найти
.
Решение.
Чтобы воспользоваться табличным
интегралом 6:
,
нужно под знаком дифференциала получить
3x. Так как
,
то умножим и разделим подынтегральное
выражение на 3. Получим
.
Использовав
свойства интеграла и введя новую
переменную
,
найдем
.
Пример:
Найти
.
Решение.
Воспользуемся табличной формулой 2. Так
как
,
то, умножив и разделив подынтегральное
выражение на 2 и введя новую переменную
,
получим:
.
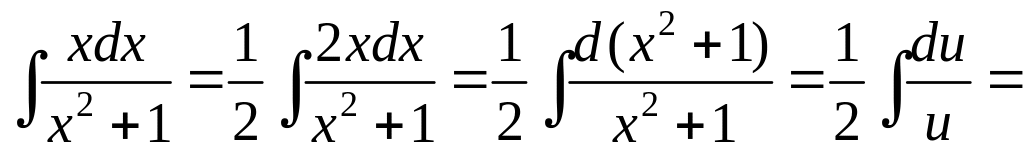
В дальнейшем переменную u можно не писать.
Пример:
Найти
.
Решение.
Воспользуемся табличной формулой 4. Так
как
,
то имеем:
.
Пример:
Найти
.
Решение.
Так как
,
то используя табличную формулу 1 при
,
получим:
.
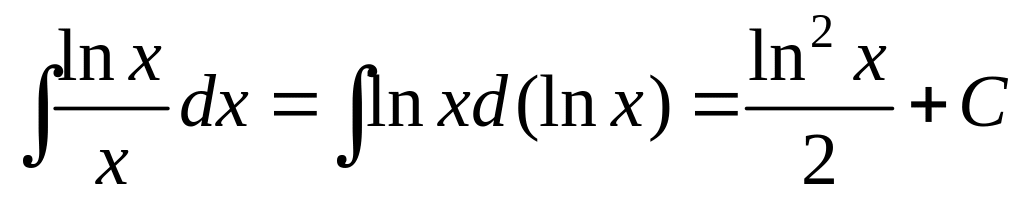Пример:
Найти
.
Решение.
Воспользуемся табличным интегралом 1
при
и формулой
.
Получим:
.
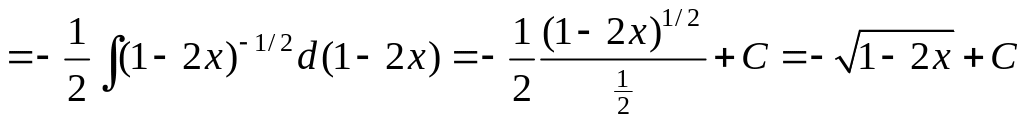Пример:
Найти
.
Решение.
.
Пример:
Найти
.
Решение.
.
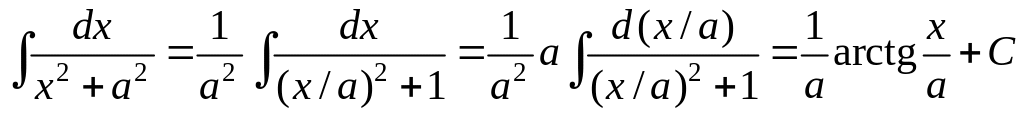Полученную формулу
следует запомнить, как табличную.
Пример:
Найти
.
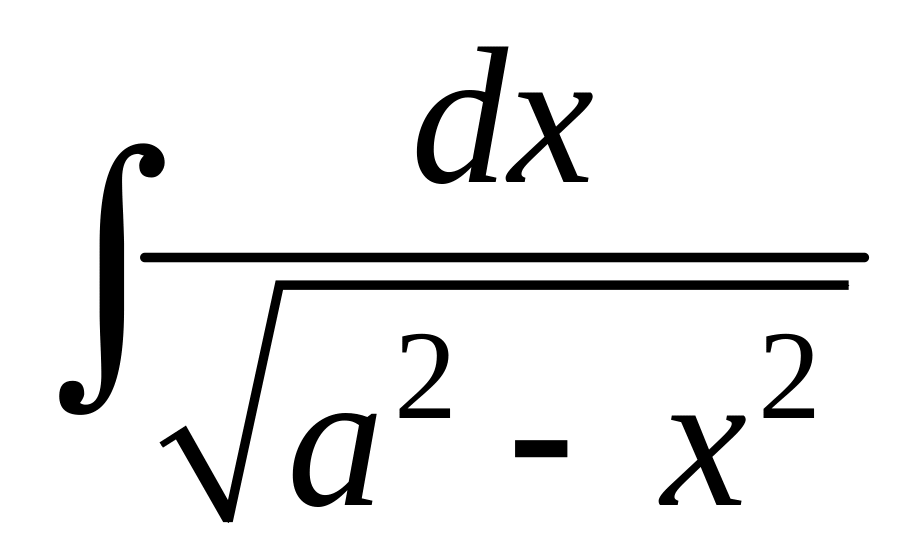Решение.
.
Полученную формулу
также следует запомнить, как табличную.
Интегрирование по частям
Пусть
и
– дифференцируемые функции переменной
x. Найдем дифференциал от их произведения
.
Проинтегрировав обе части этого
равенства, получим
.
Определение. Формула
называется формулой интегрирования по частям.
Чтобы
применить эту формулу, подынтегральное
выражение
представим в виде произведения
.
Тогда вычисление исходного интеграла
сведется к нахождению двух других
интегралов:
и
.
Поэтому необходимо так выбрать выражения
u и
,
чтобы два новых интеграла оказались
более простыми, чем исходный.
Пример:
Найти
.
Решение.
Положим
,
.
Тогда
,
(берем только первообразную при
).
Используя формулу интегрирования по
частям, получим
.
Пример:
Найти
.
Решение.
Положим
.
Тогда
.
Метод интегрирования по частям применяется для интегрирования произведения функций. Например, в интегралах вида
,
,
,
— целое,
выбирается
,
а в интегралах вида
,
,
в
качестве u берутся функции
,
,
,
соответственно (Почему?).
С помощью интегрирования по частям берутся также интегралы от основных элементарных функций, которых нет в таблице:
,
,
.
Формулу интегрирования по частям в одном примере можно применять несколько раз.
Метод замены переменной (метод подстановки)
Пусть требуется найти интеграл
.
Допустим,
что
– неизвестная первообразная (
),
которую надо найти. Сделаем замену
переменной, положив
.
Тогда функция
станет сложной функцией переменной t.
Следовательно,
.
Проинтегрировав правую и левую части полученного равенства по t, получим
или
.
Учитывая, что – первообразная для функции , окончательно получаем формулу:
,
которая называется формулой замены переменной.
Использование
этой формулы заключается в следующем:
по виду подынтегрального выражения
выбирают замену переменной
(на практике обычно выбирают
,
а затем выражают
)
и согласно формулы замены переменной
переходят к новому интегралу по переменной
t. Этот интеграл вычисляют, а затем
возвращаются к старой переменной x,
подставляя в ответ
.
Пример:
Найти
.
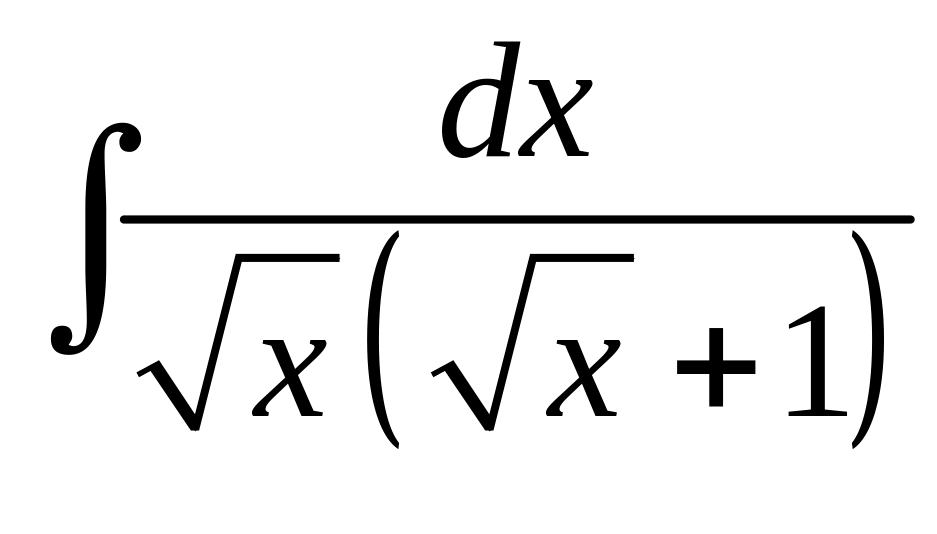Решение.
Положим
.
Тогда
.
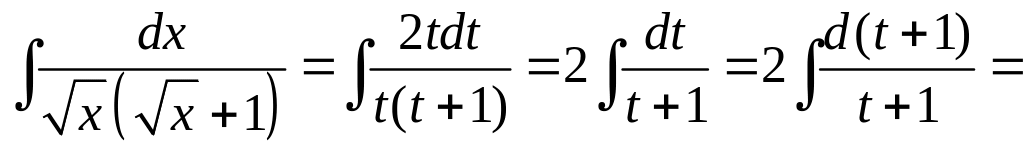