6. Методы интегрирования

Замена переменной в определенном интеграле

1. Пусть дан

,

где  – непрерывная на [ ] функция. Пусть , причем удовлетворяет условиям:

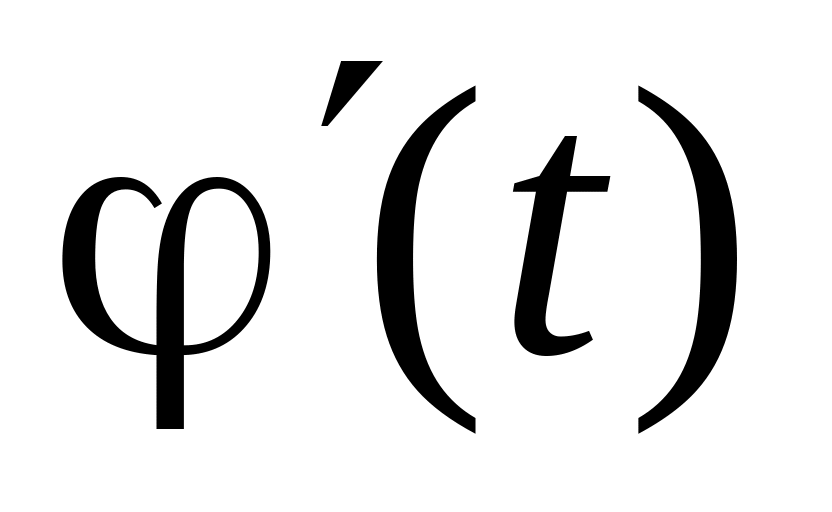1. , непрерывны на [ ],

2. , .

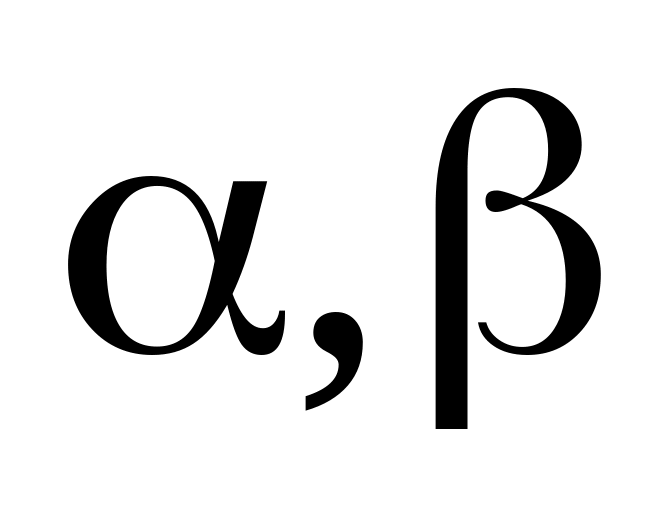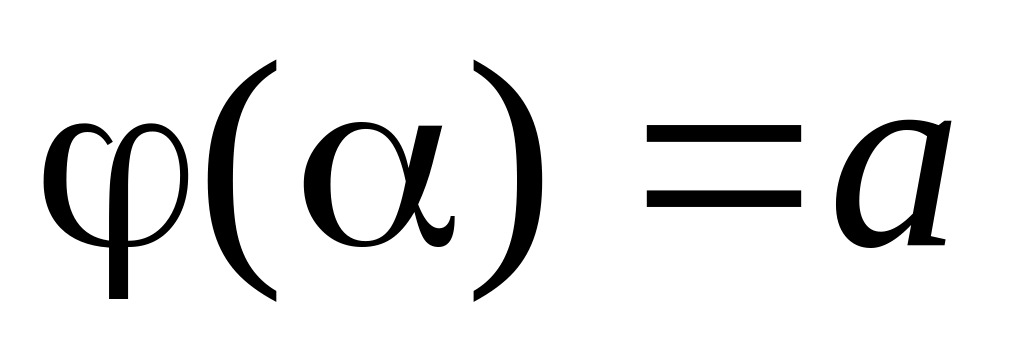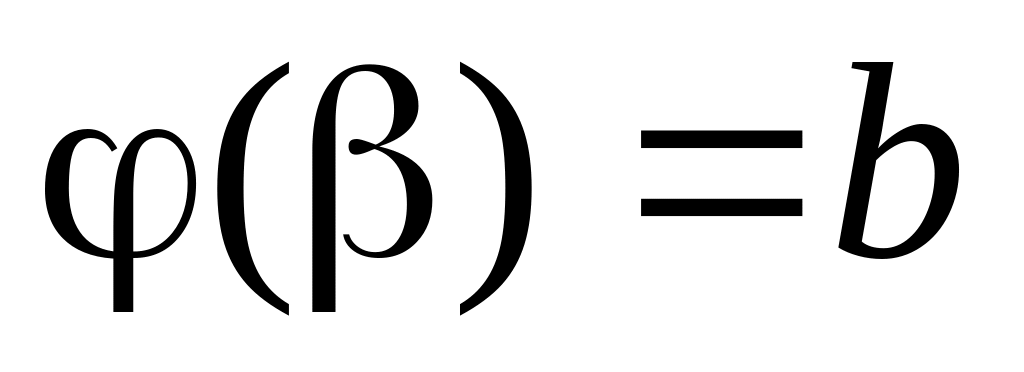Тогда имеет место формула

.

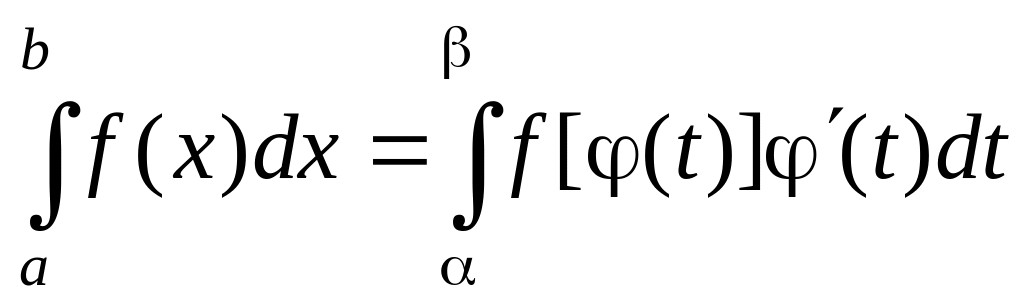1. Сравним доказанную формулу с формулой замены переменной в неопределенном интеграле. Подынтегральные функции в этих формулах совпадают, отличия состоят в следующем:

1. в определенном интеграле обязательна смена пределов интегрирования по формулам , ;

2. после вычисления неопределенного интеграла необходимо вернуться к старой переменной, в определенном интеграле этого делать не нужно.

Примеры.

1. Найти .

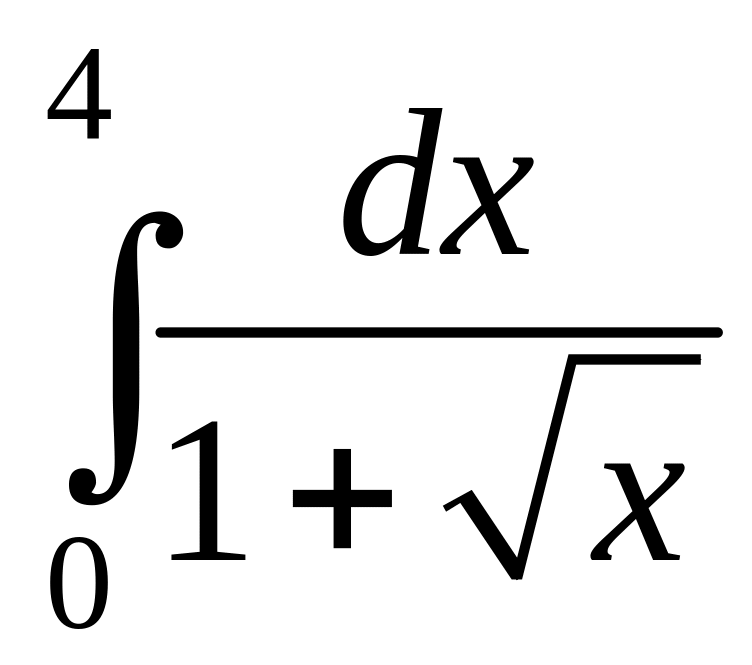Решение. Положим , , , . Тогда

.

2. Найти .

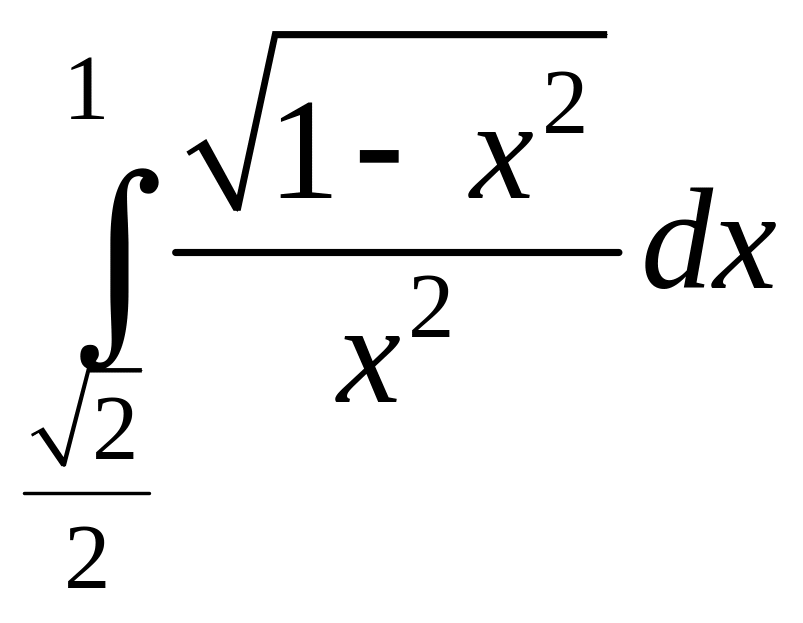3. Решение. Положим , .

.

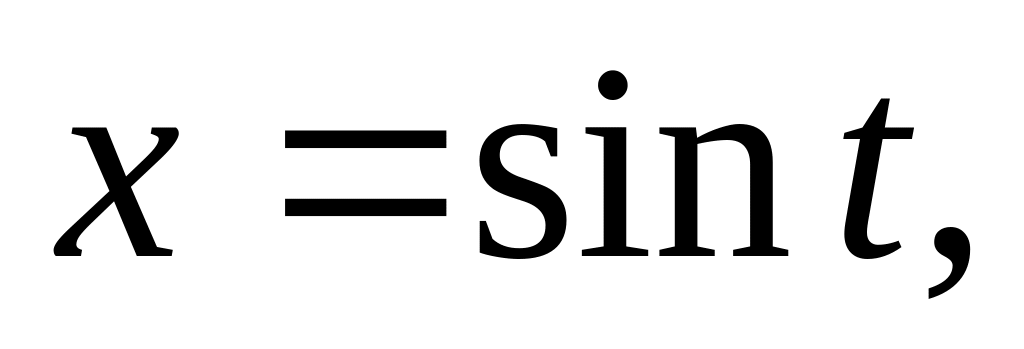
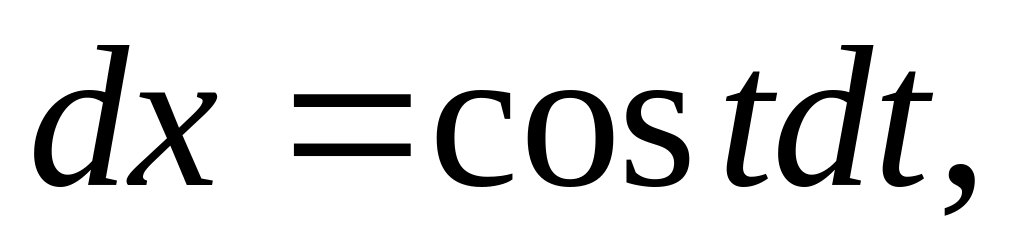
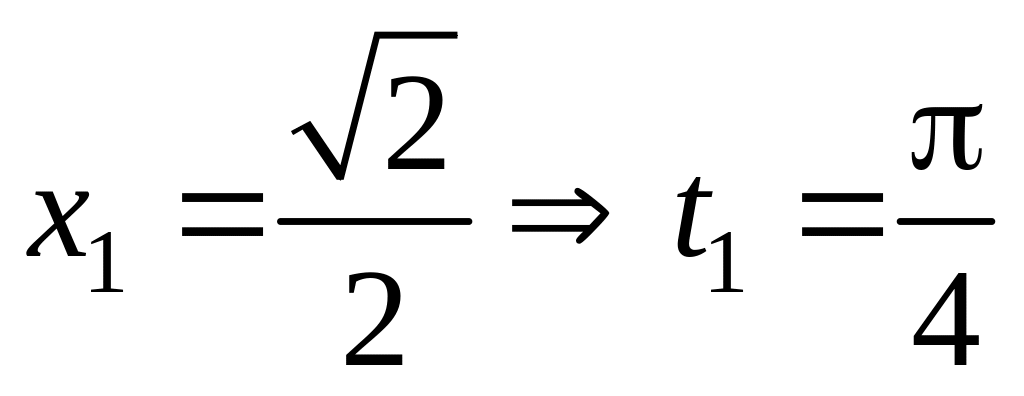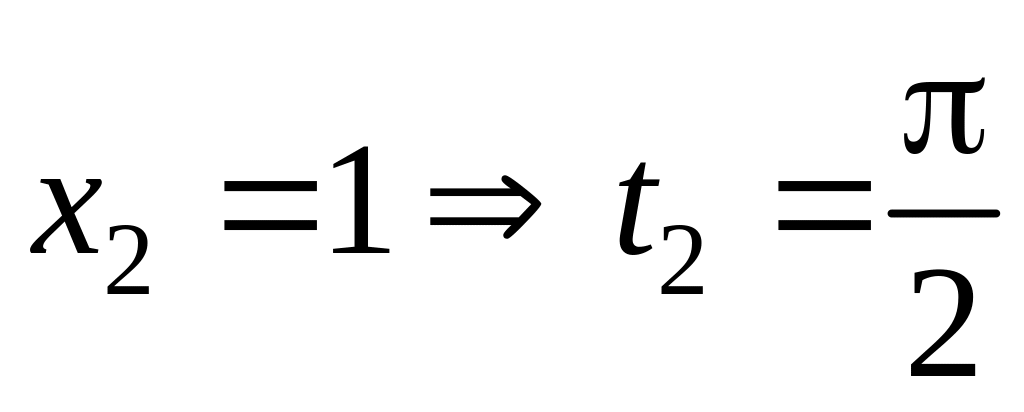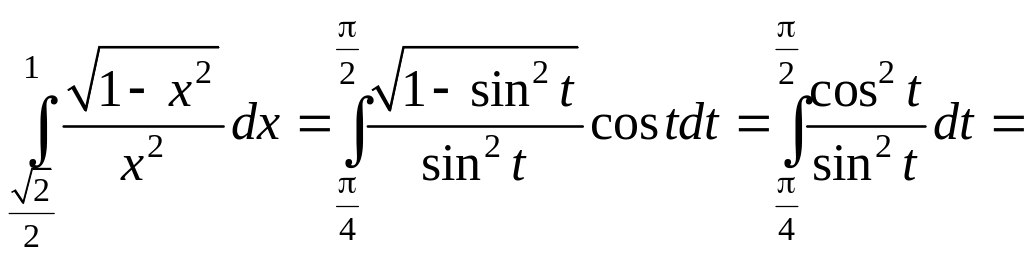
Интегрирование по частям в определенном интеграле

1. Если 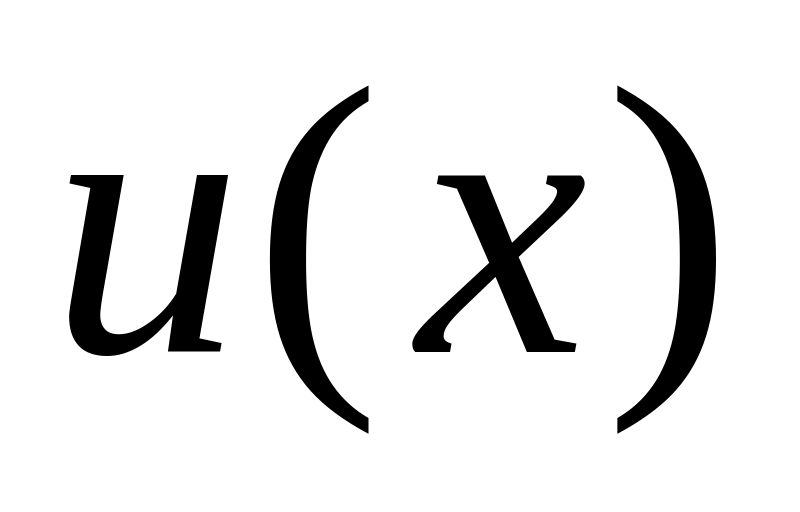, , ,  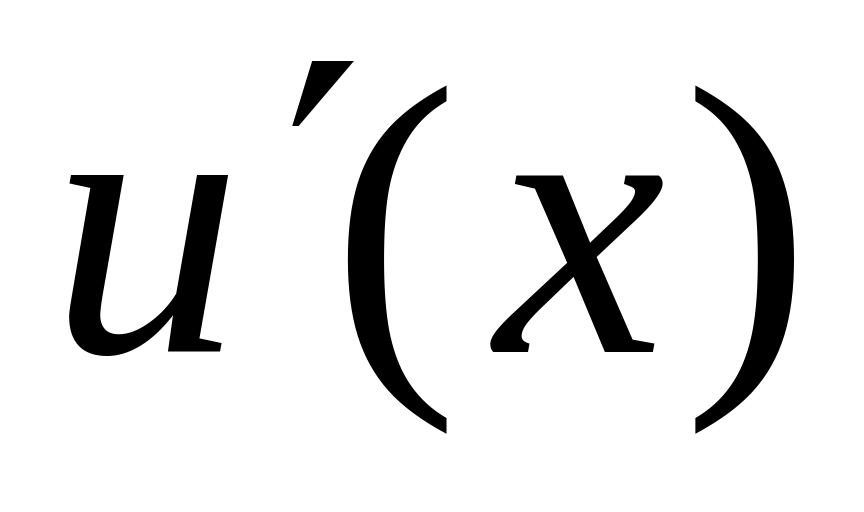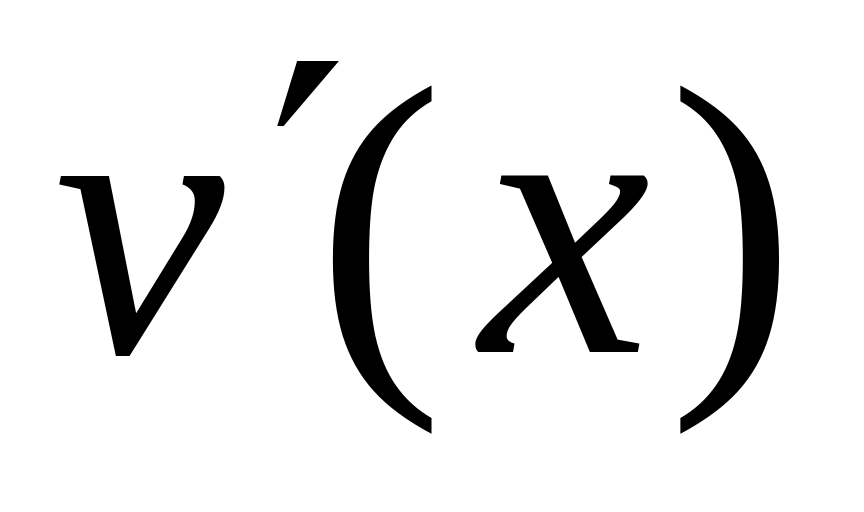– непрерывны на отрезке [ ], то имеет место формула

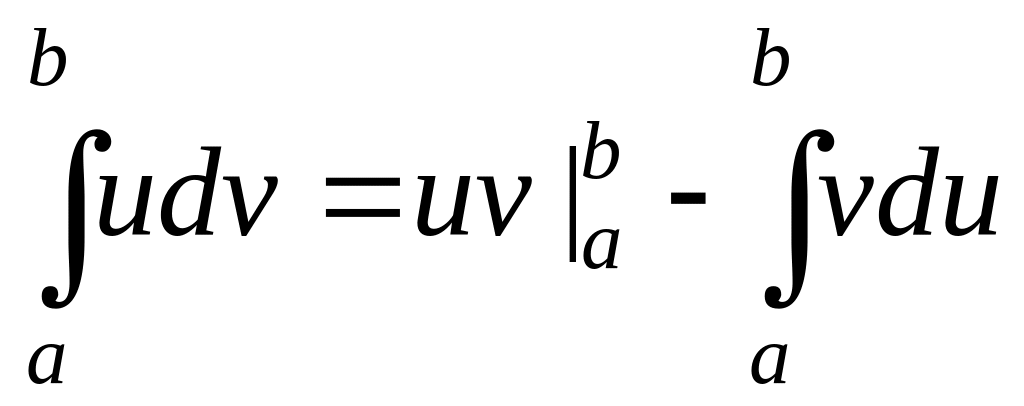
Пример.

Найти .

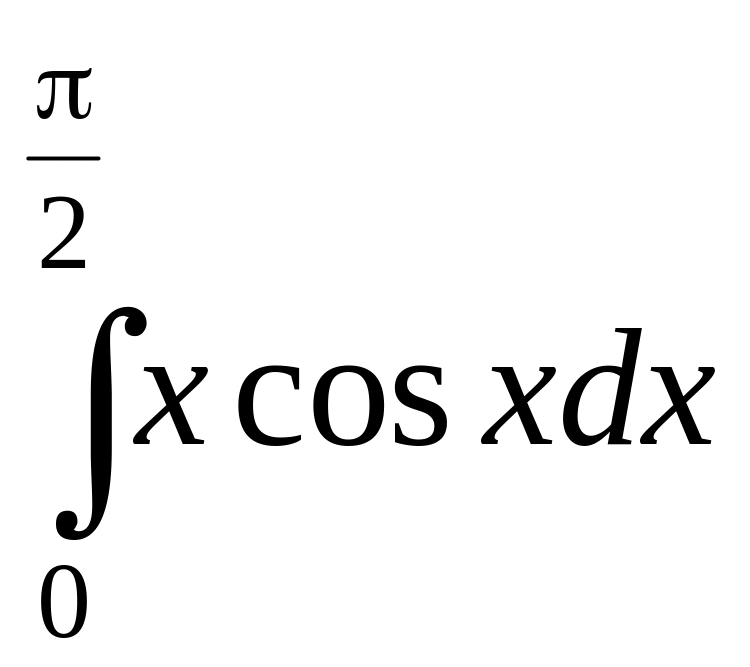Решение. Пусть , , , .

.

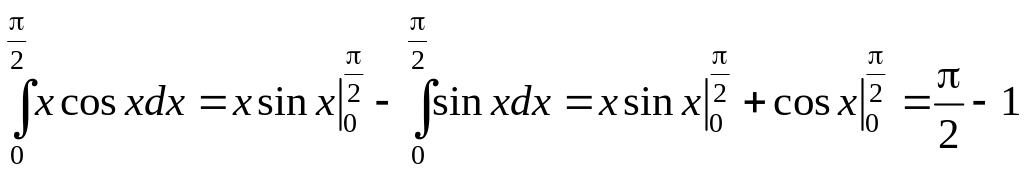6. Несобственные интегралы с бесконечными пределами.

При введении понятия определенного интеграла считалось, что отрезок конечный, а функция непрерывна на и, следовательно, ограничена. Если нарушено хотя бы одно из перечисленных условий, то определить интеграл, как предел интегральных сумм нельзя. Однако, имеется другой способ обобщить понятие определенного интеграла на случаи, когда:

1. интервал интегрирования бесконечный,

2. подынтегральная функция неограниченная.

Такие интегралы называются несобственными интегралами.

Определение несобственных интегралов

Пусть функция непрерывна на участке оси 0x. Выберем произвольное значение и рассмотрим определенный интеграл 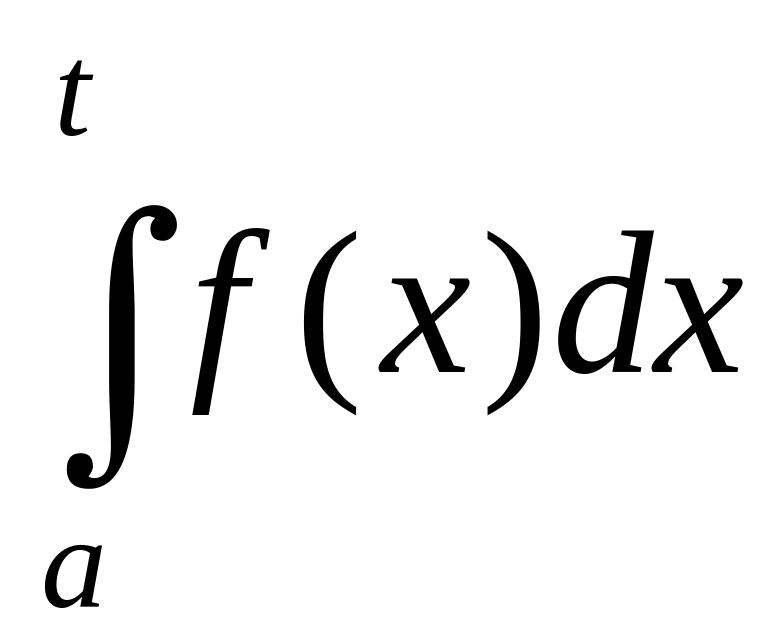на конечном отрезке .

Определение. Несобственным интегралом от функции на промежутке называется

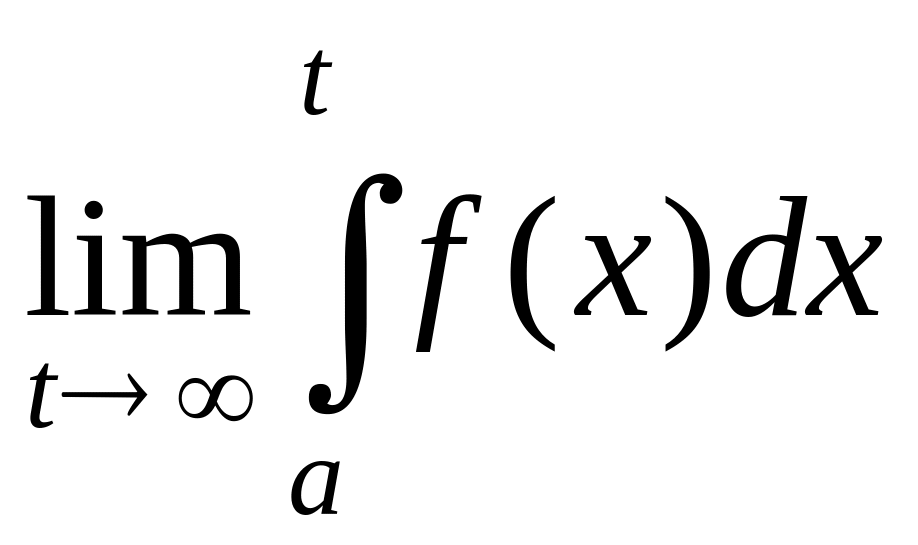
и обозначается 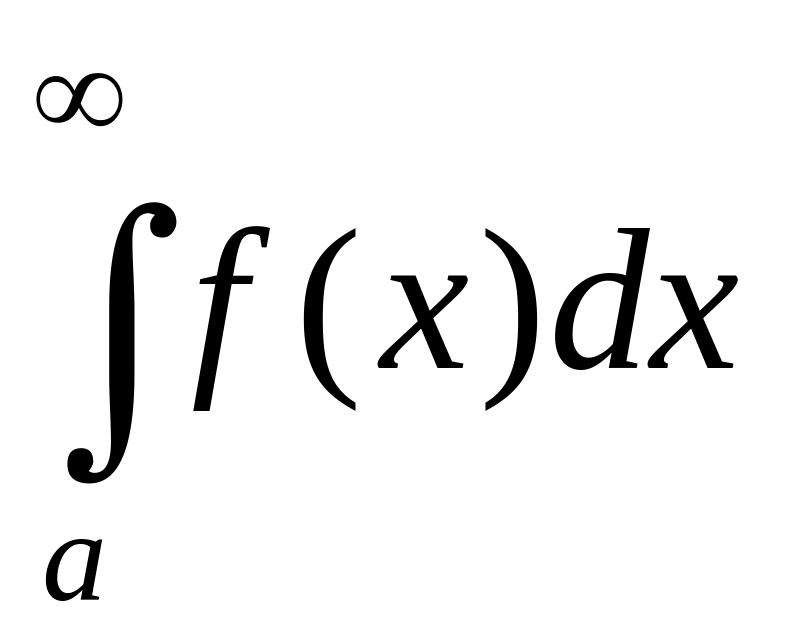. Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то — расходящимся.

Итак, по определению

.

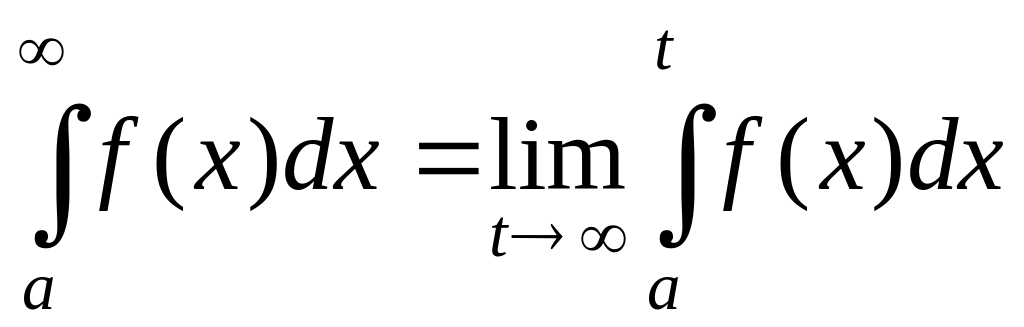Геометрический смысл несобственного интеграла. Если , то — это площадь бесконечной криволинейной трапеции с основанием (рис.7).

Рис.7

Аналогично определяется несобственный интеграл от функции на промежутке :

.

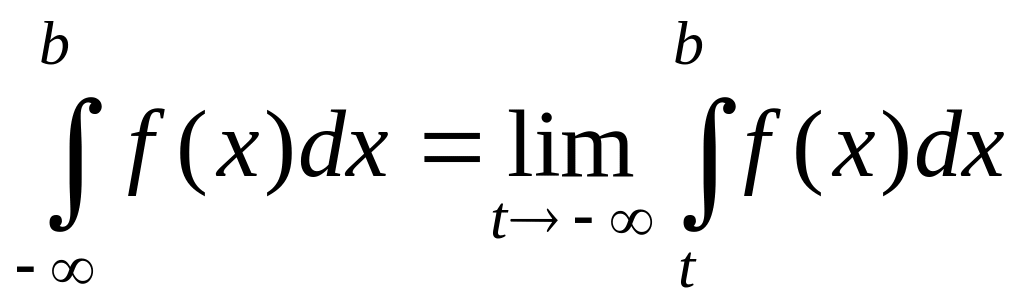Если функция непрерывна на всей числовой оси , то можно определить несобственный интеграл 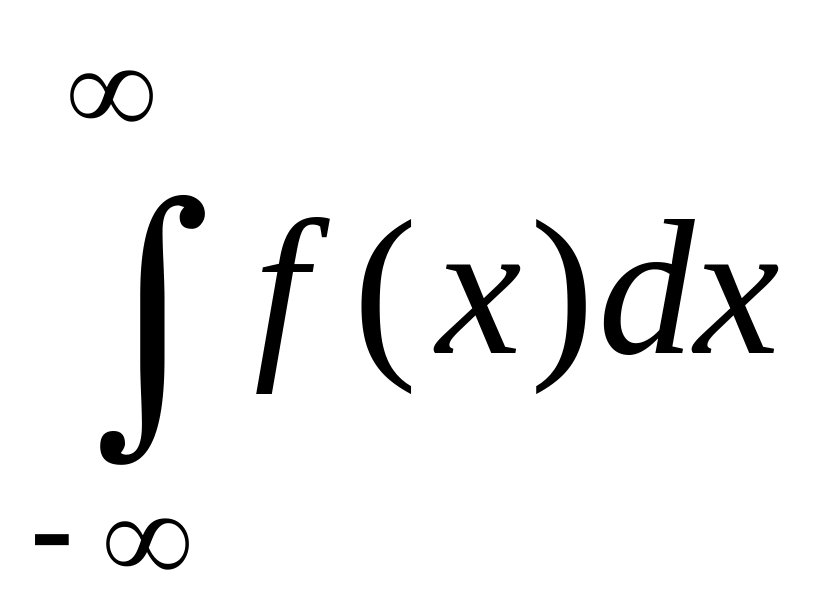. Для этого выберем произвольную точку c, а несобственный интеграл по промежутку определим по формуле

.

Несобственный интеграл называется сходящимся, если сходятся оба интеграла, стоящие в правой части формулы, и расходящимся, если расходится хотя бы один из них.

Вычисление несобственных интегралов

Пусть — первообразная для функции . Тогда, используя определение несобственного интеграла и формулу Ньютона-Лейбница, получим

,

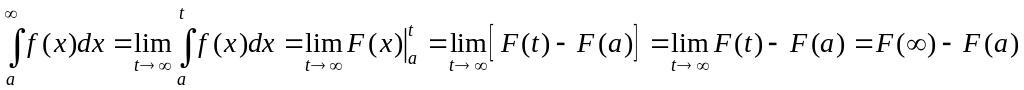где .

Таким образом, для вычисления несобственного интеграла получена формула Ньютона-Лейбница

.

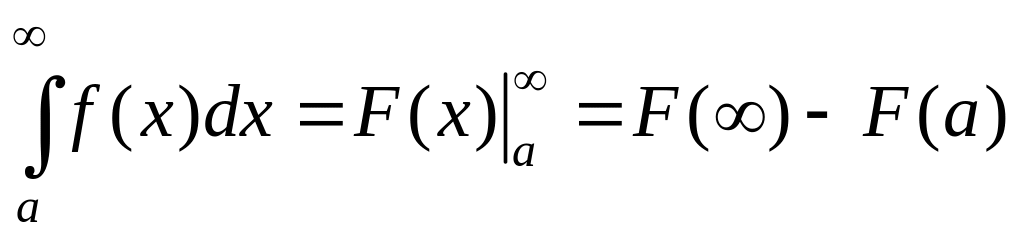Аналогично,

,

.

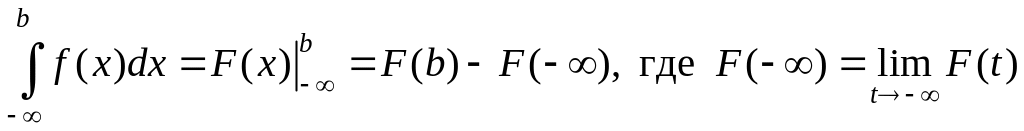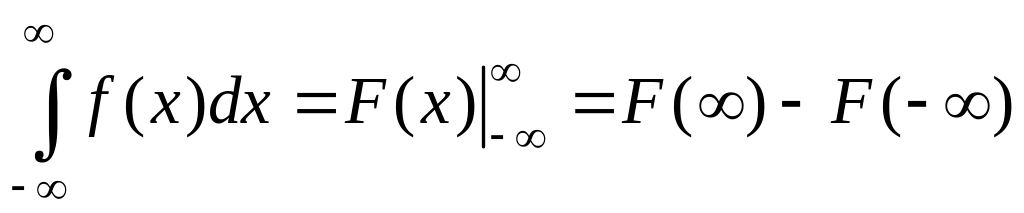Примеры.

1. Найти .

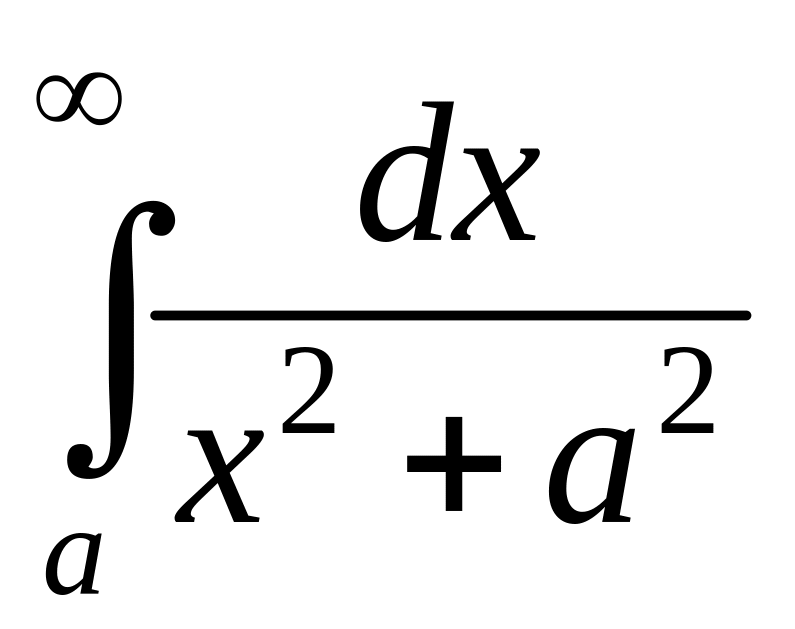Решение.

.

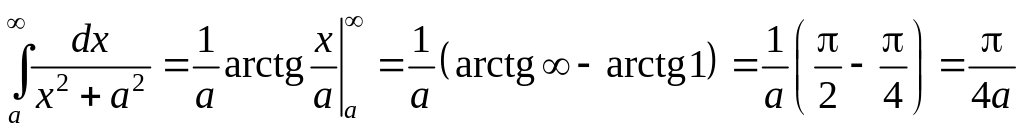Интеграл сходится.

2. Найти .

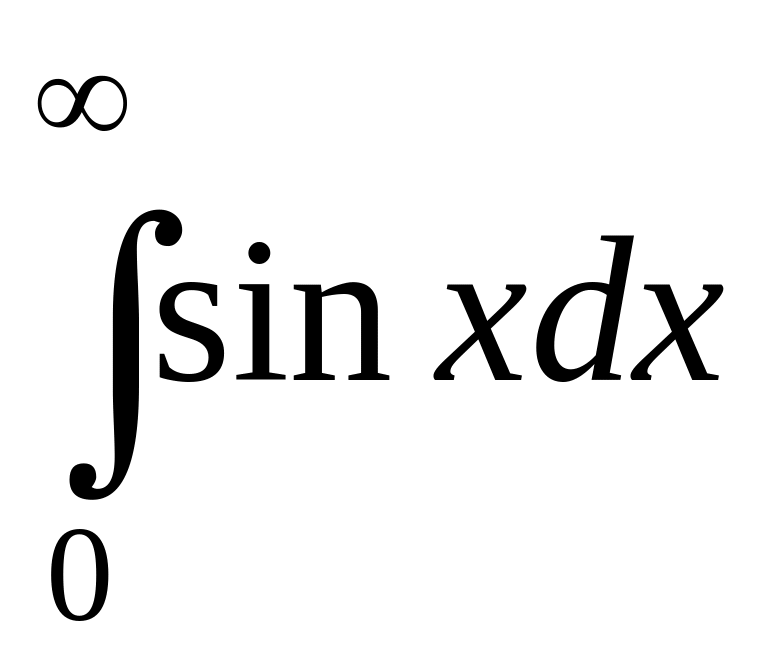Решение.

.

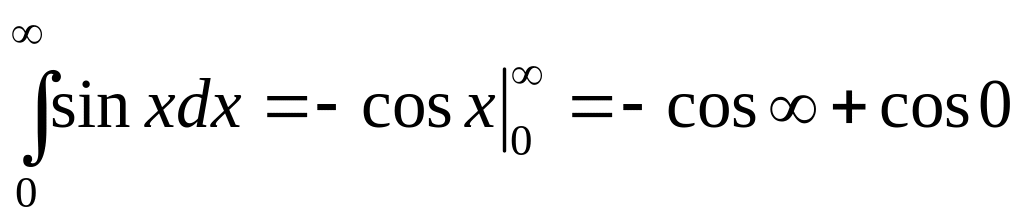Интеграл расходится, так как не существует.

Исследование сходимости интеграла

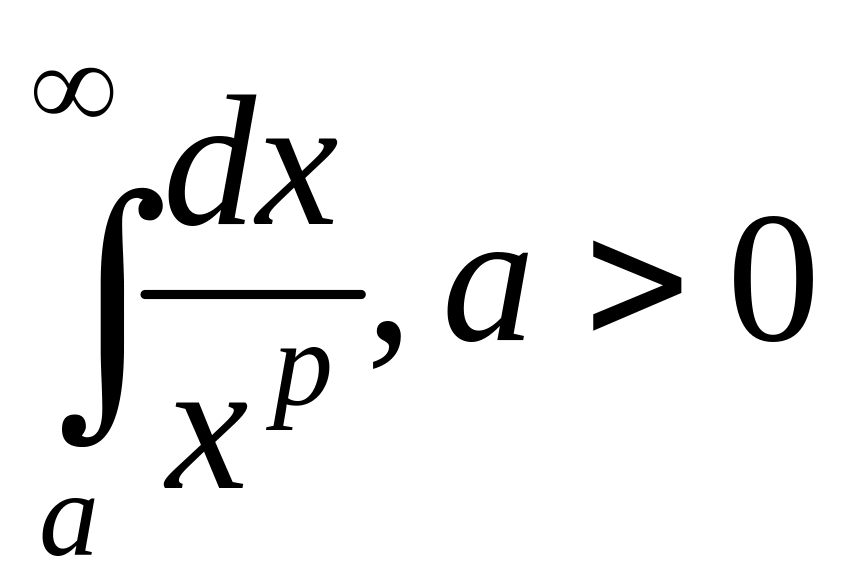
При дальнейшем изучении курса высшей математики часто будут использоваться несобственные интегралы вида . Поэтому проведем исследование его сходимости в зависимости от величины параметра p.

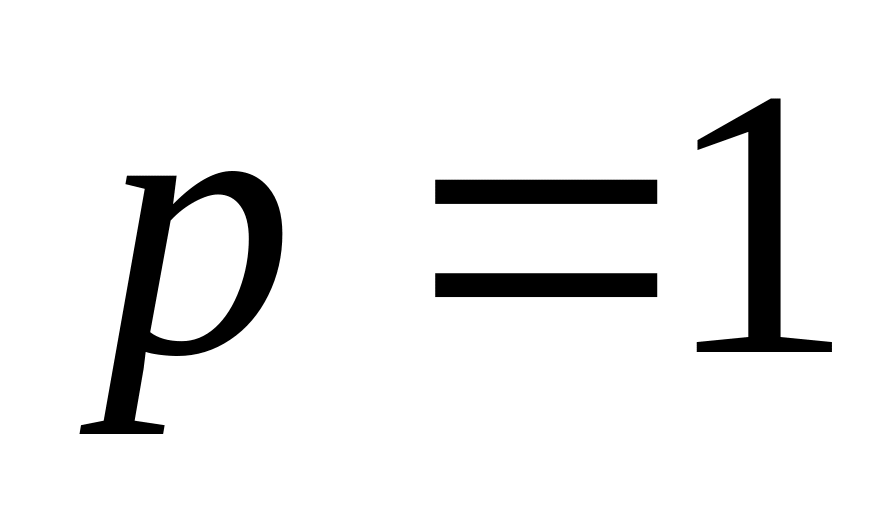1. Пусть . Тогда

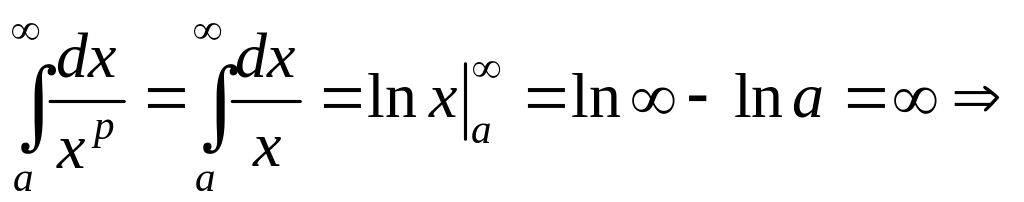интеграл расходится.

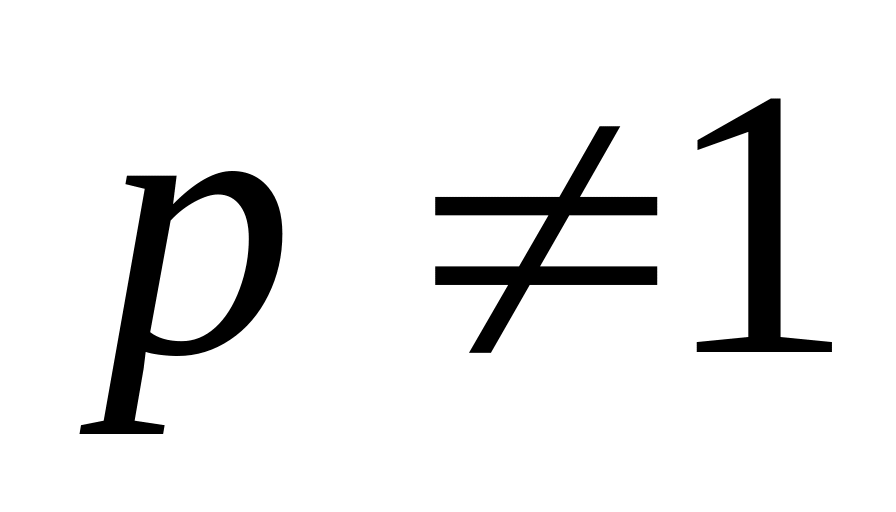2. Пусть . Тогда

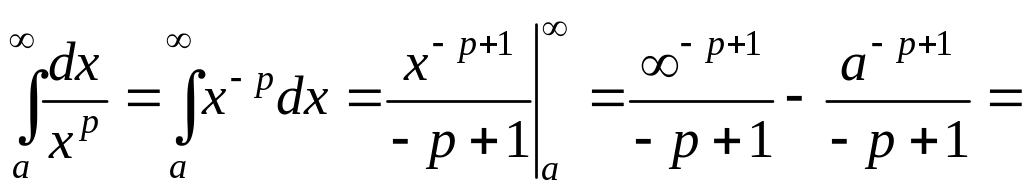
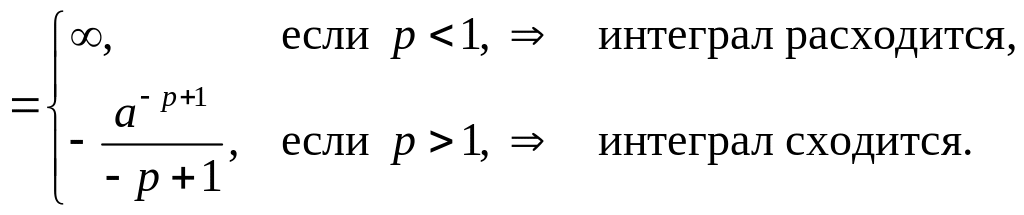
Итак,