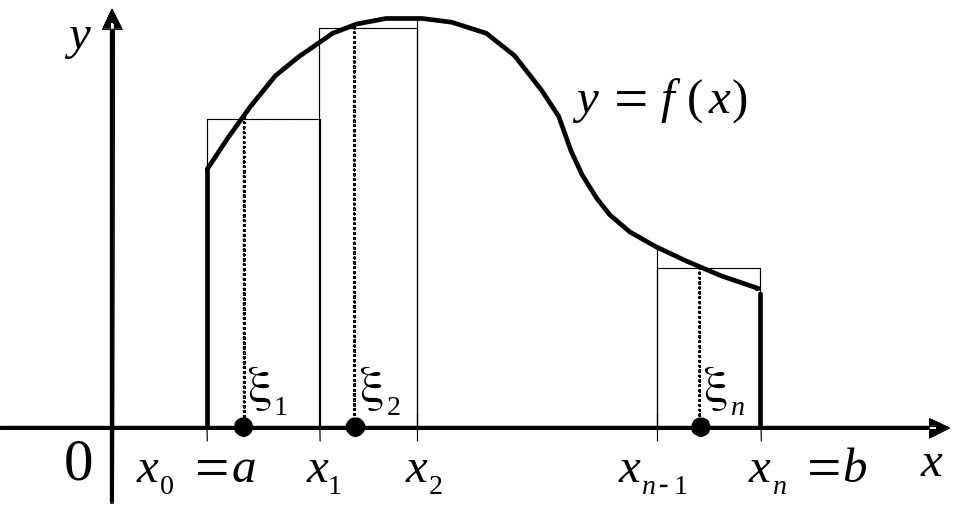- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
Определенный интеграл
Опорный конспект
1. Определение
О:
|
2. Свойства
30.
40.
|
3. Формула Ньютона-Лейбница
Замена переменной
Интегрирование по частям
|
|
|
|
5 Геометрические приложения
Площадь
фигуры
О
|
|
4 Несобственные интегралы с бесконечными пределами
О:
|
Задача о вычислении площади криволинейной трапеции
Прежде, чем перейти к постановке и решению задачи, дадим определение.
Определение.
Криволинейной трапецией
называется плоская фигура, ограниченная
осью 0x,
вертикальными прямыми
|
Рис.3. |
Постановка задачи. Найти площадь криволинейной трапеции, ограниченной осью 0x, вертикальными прямыми , и графиком функции , , .
Решение
задачи. В
частном
случае, когда
![]() ,
криволинейная трапеция является
прямоугольником с основанием
,
криволинейная трапеция является
прямоугольником с основанием
![]() и высотой C,
а ее площадь находится по формуле
и высотой C,
а ее площадь находится по формуле
![]() .
.
Больший интерес представляет общий случай, когда функция отлична от постоянной, то есть .
Основание трапеции – отрезок
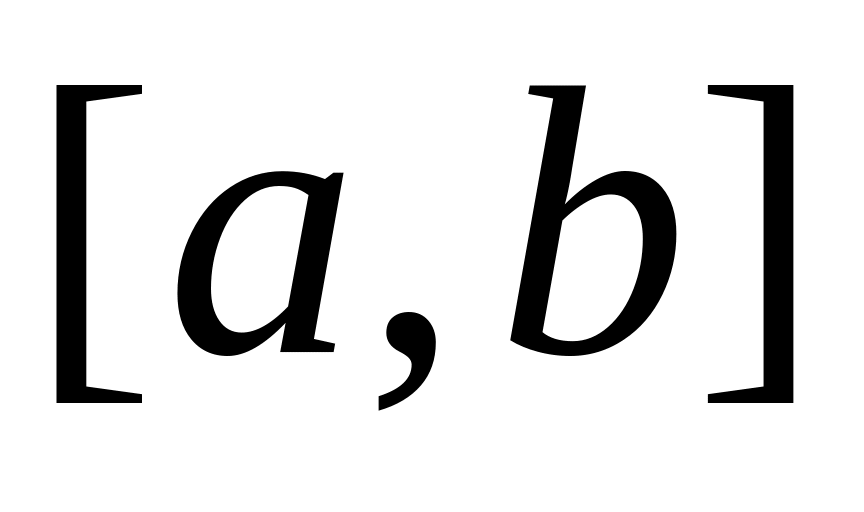 оси 0x
разобьем произвольным образом на n
частей:
оси 0x
разобьем произвольным образом на n
частей:
 ,
,
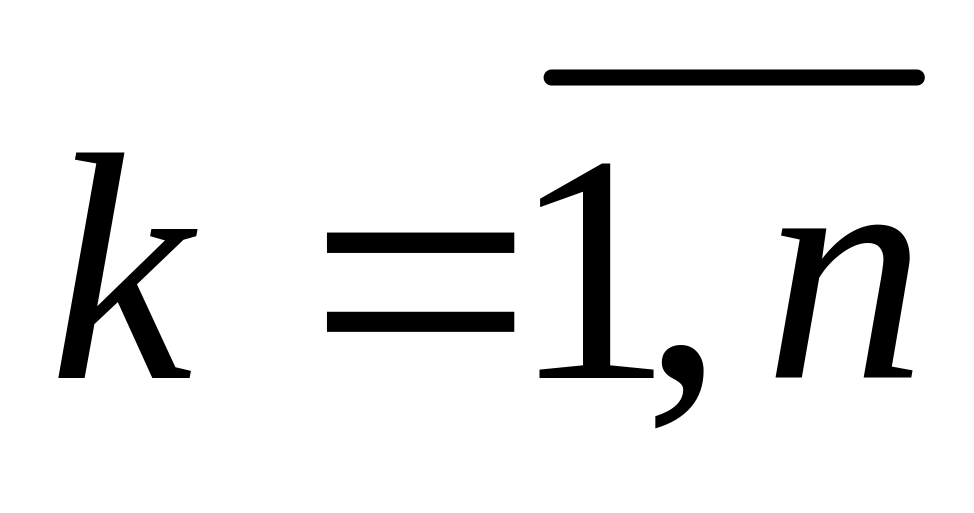 ,
длины которых обозначим через
,
длины которых обозначим через
 .
Проведем через точки деления прямые,
параллельные оси 0y.
Тогда криволинейная трапеция разобьется
на n
полосок.
.
Проведем через точки деления прямые,
параллельные оси 0y.
Тогда криволинейная трапеция разобьется
на n
полосок.Выберем произвольно точки
 ,
и найдем значения функции
в этих точках:
,
и найдем значения функции
в этих точках:
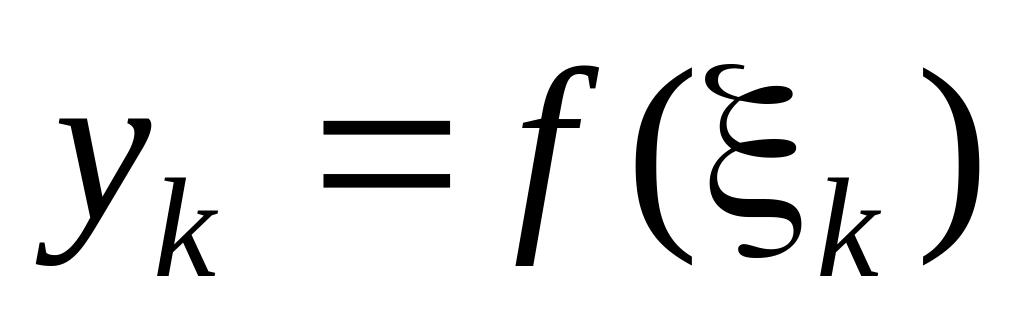 .
.Найдем площадь
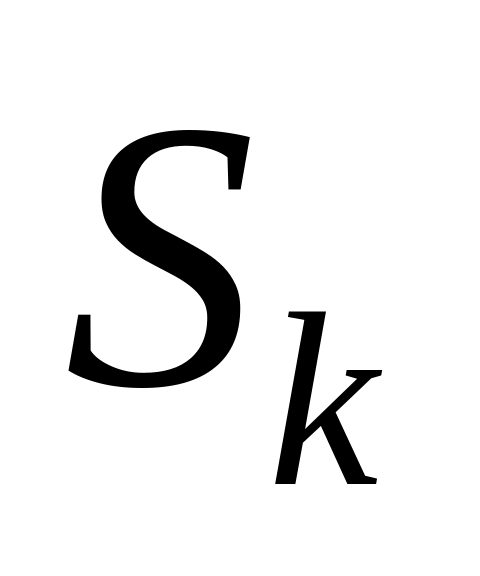 каждой k-ой
полоски приближенно,
считая полоску прямоугольником с
высотой
каждой k-ой
полоски приближенно,
считая полоску прямоугольником с
высотой
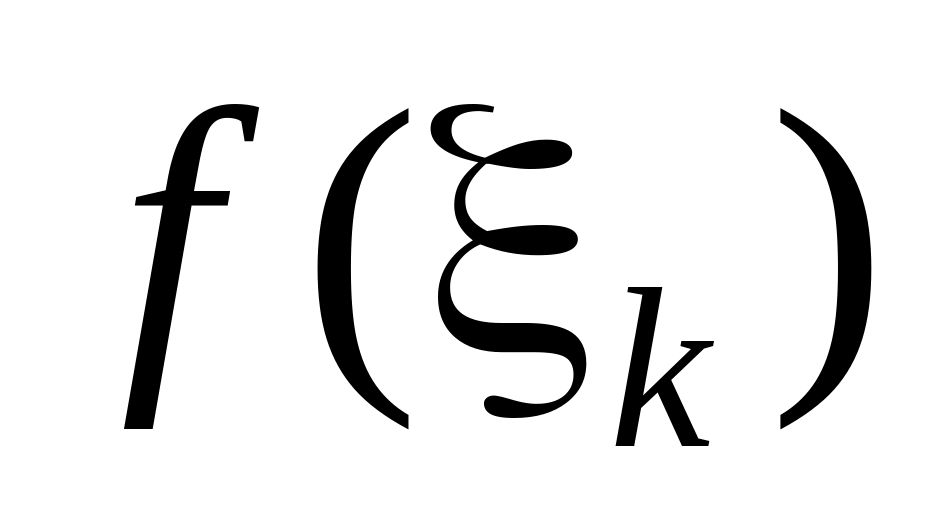 и основанием
.
Тогда
и основанием
.
Тогда
![]() ,
,
а площадь всей криволинейной трапеции найдется по приближенной формуле
![]() .
.
Перейдя к пределу при стремлении максимальной длины участка разбиения отрезка к нулю, получим точную формулу для площади криволинейной трапеции
![]() .
.
Определенный интеграл как предел интегральных сумм. Геометрический и механический смысл определенного интергала.
Рассмотрим функцию на отрезке и выполним следующие построения.
Разобьем отрезок произвольным образом на n частей: , , (здесь
 ,
,
 )
и положим
)
и положим
 ,
.
,
.В каждом отрезке выберем произвольную точку
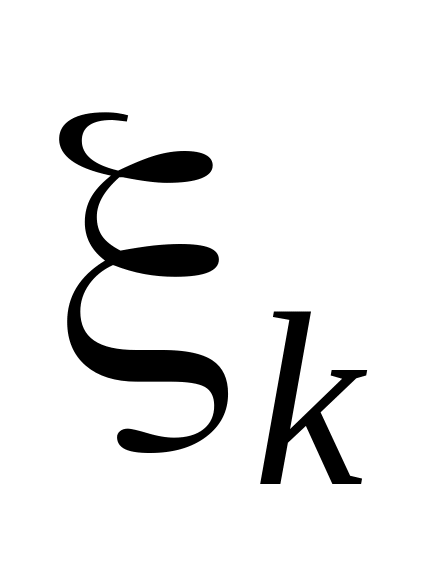 и найдем значения функции
.
и найдем значения функции
.Составим сумму
![]() .
.
Эта сумма называется интегральной суммой для функции на отрезке . Она зависит от способа разбиения отрезка на части и от выбора точек .
Определение.
Если существует конечный предел
последовательности интегральных сумм
при
![]() ,
не зависящий ни от способа разбиения
отрезка
на части, ни от выбора точек
,
то этот предел называется определенным
интегралом
от функции
на отрезке
и обозначается
,
не зависящий ни от способа разбиения
отрезка
на части, ни от выбора точек
,
то этот предел называется определенным
интегралом
от функции
на отрезке
и обозначается
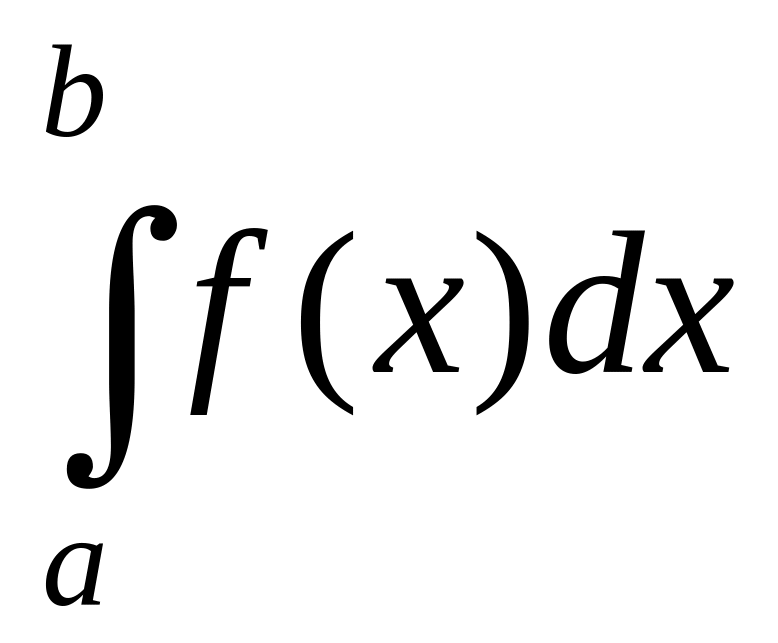 .
.
Таким образом, по определению
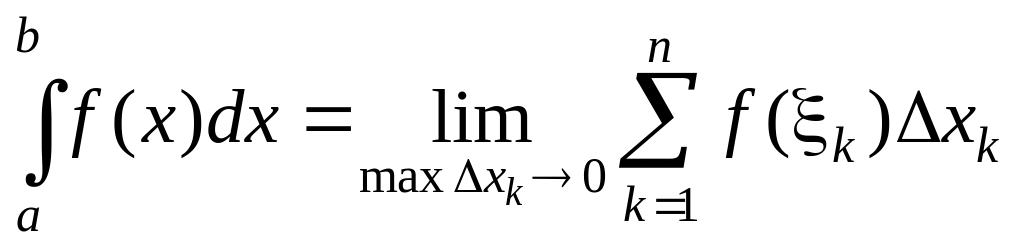 .
.
Число a называется нижним пределом интегрирования, b – верхним пределом интегрирования, отрезок – отрезком интегрирования.
Теорема существования определенного интеграла
Определение. Функция называется интегрируемой на отрезке , если существует как предел последовательности интегральных сумм.
Возникает вопрос: какими свойствами должна обладать функция, чтобы она была интегрируемой? Ответ на этот вопрос дает следующая теорема, которую примем без доказательства.
О существовании определенного интеграла. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.
Основные свойства определенного интеграла
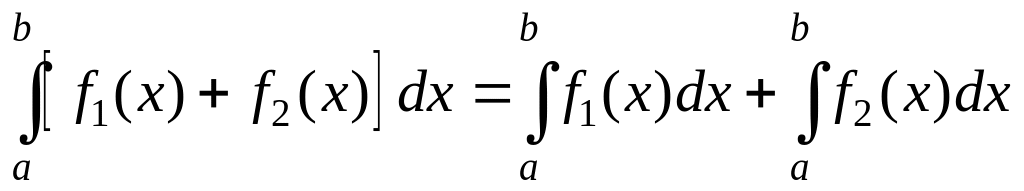
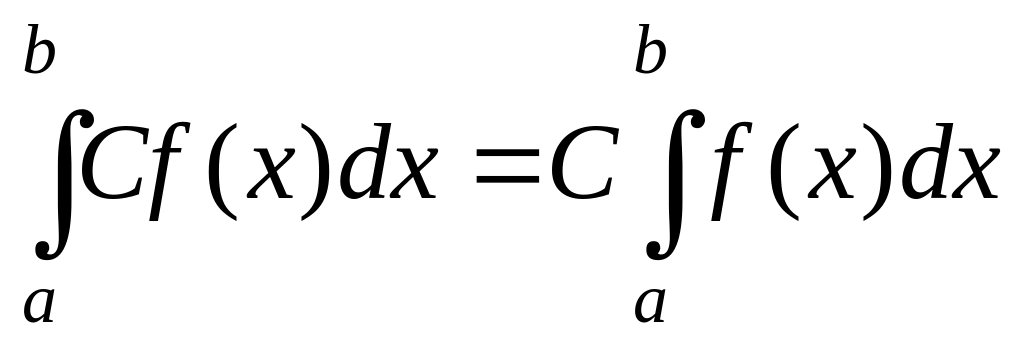 ,
,
![]() .
.
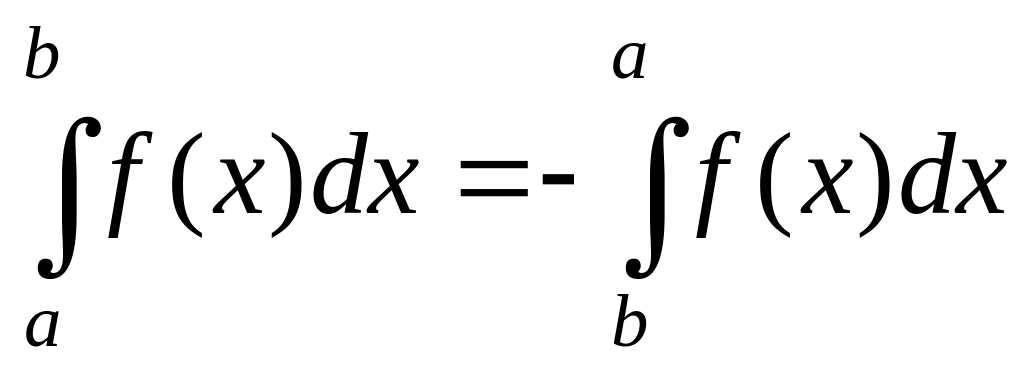 ,
,
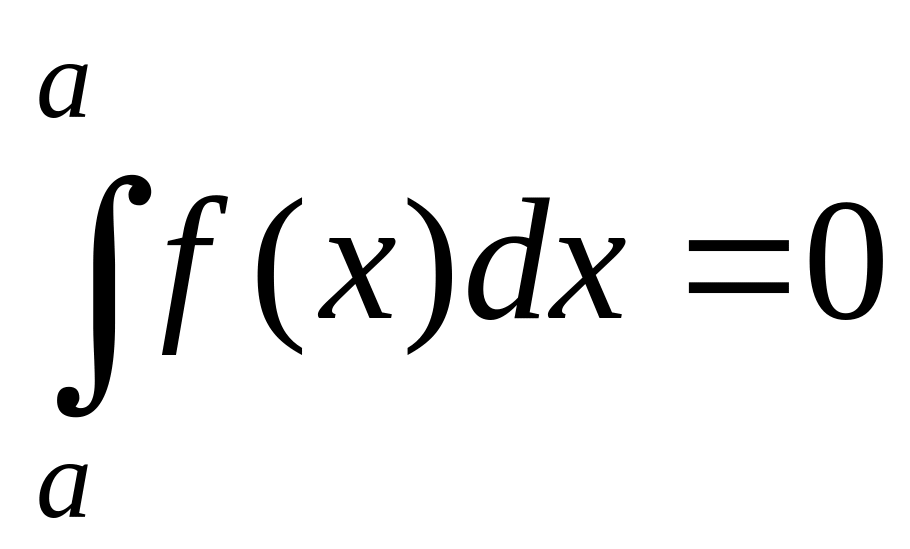
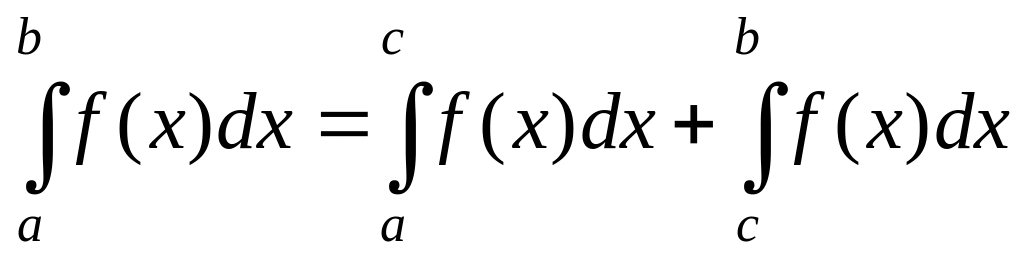
Формула Ньютона-Лейбница.
Если F(x) — какая-то первообразная непрерывной функции
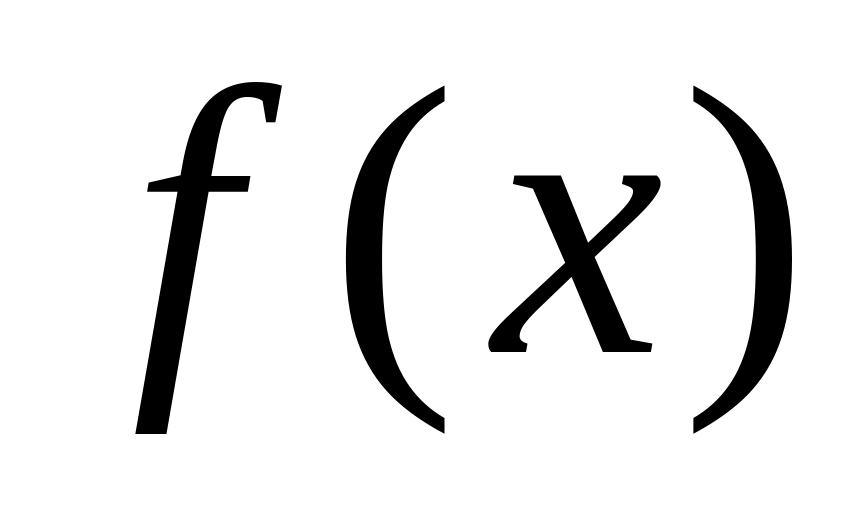 ,
то справедлива формула
,
то справедлива формула
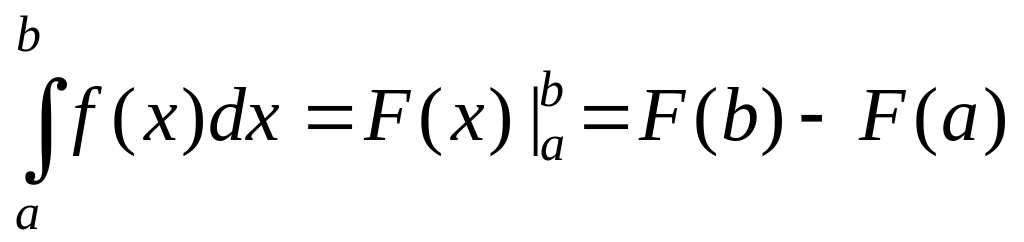
Эта формула называется формулой Ньютона—Лейбница.
Примеры.
1.
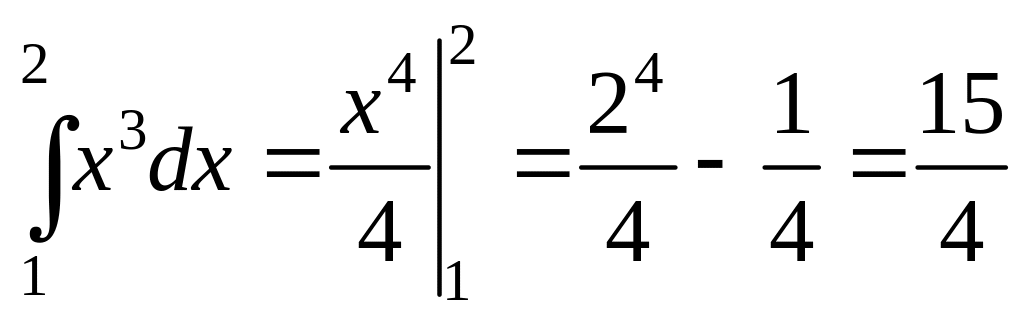 .
.
2.
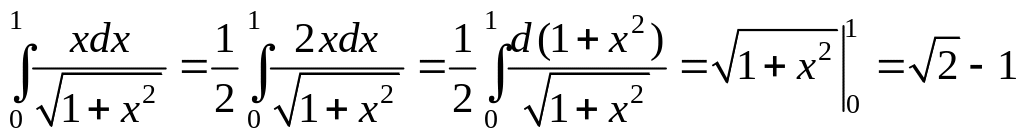 .
.

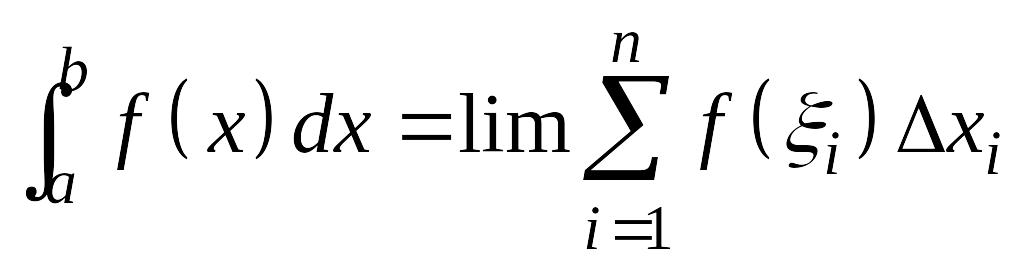 ,
, ,
,

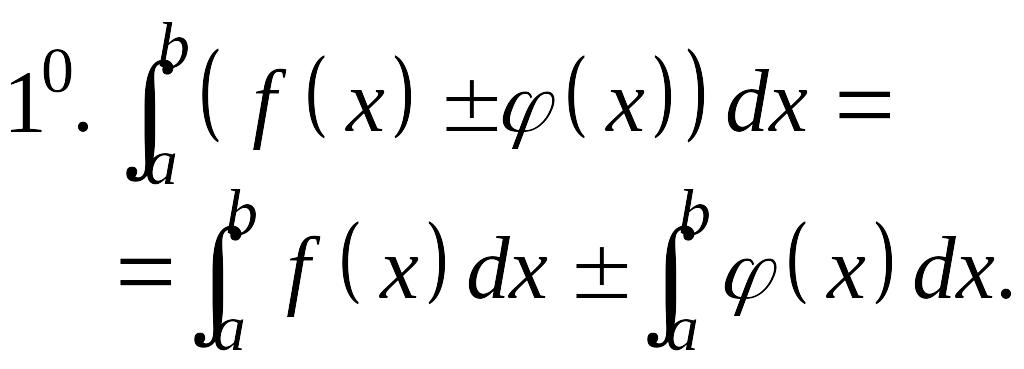
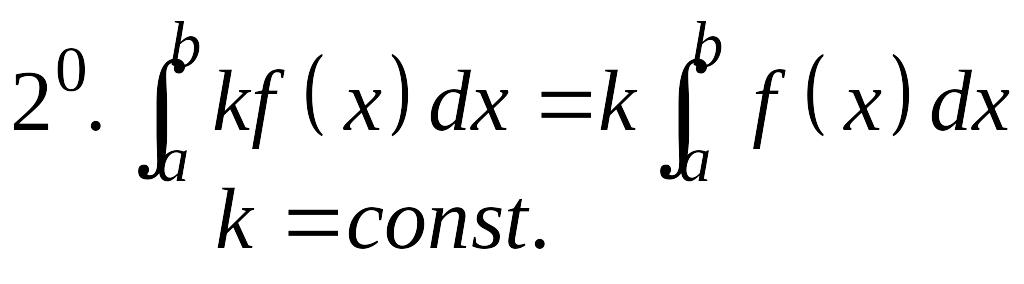
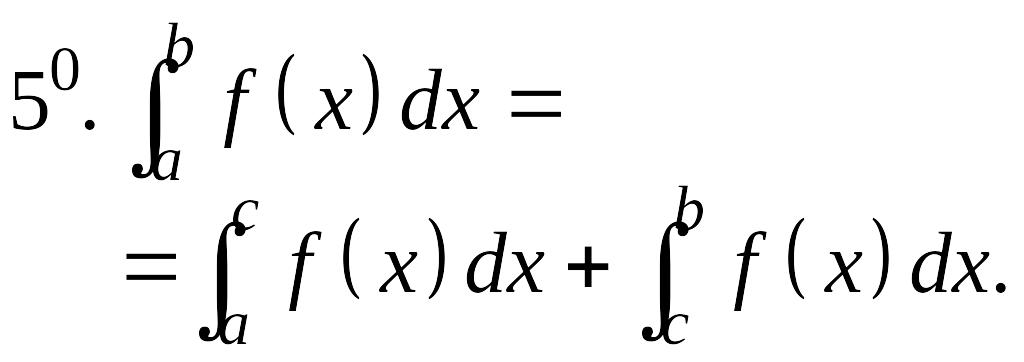
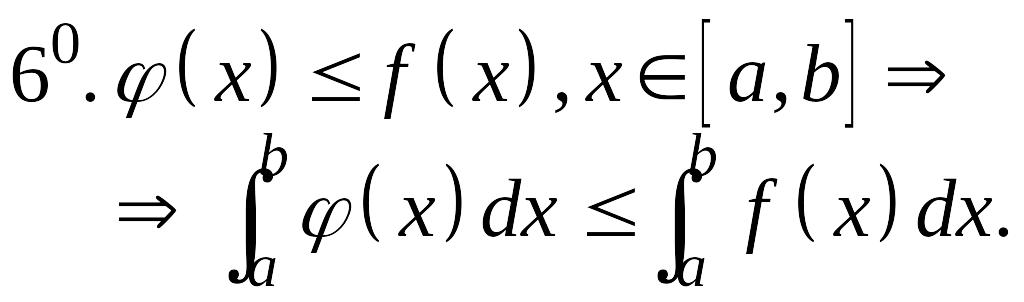
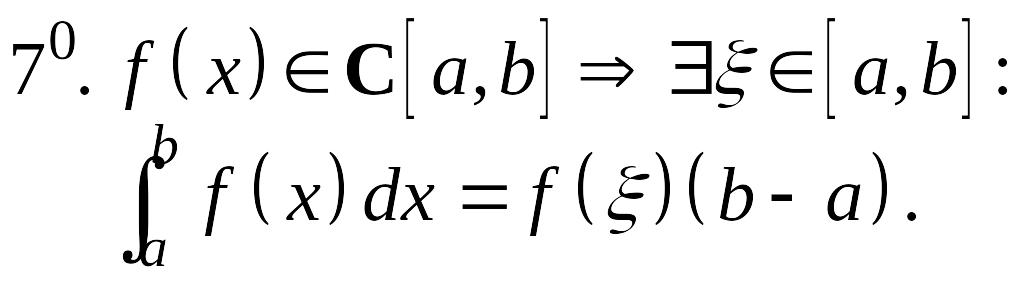
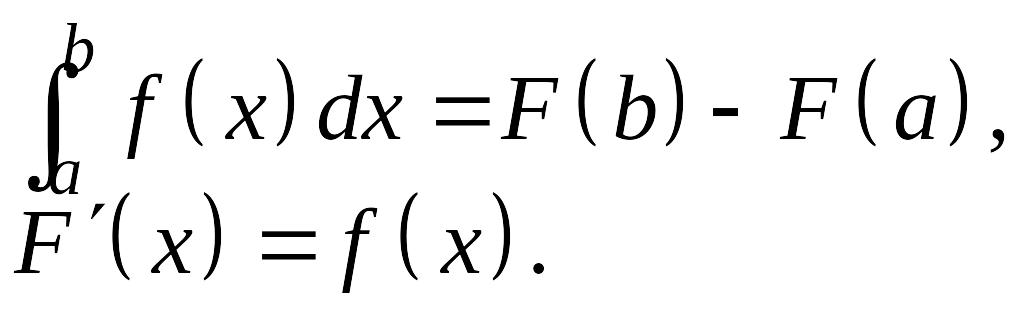
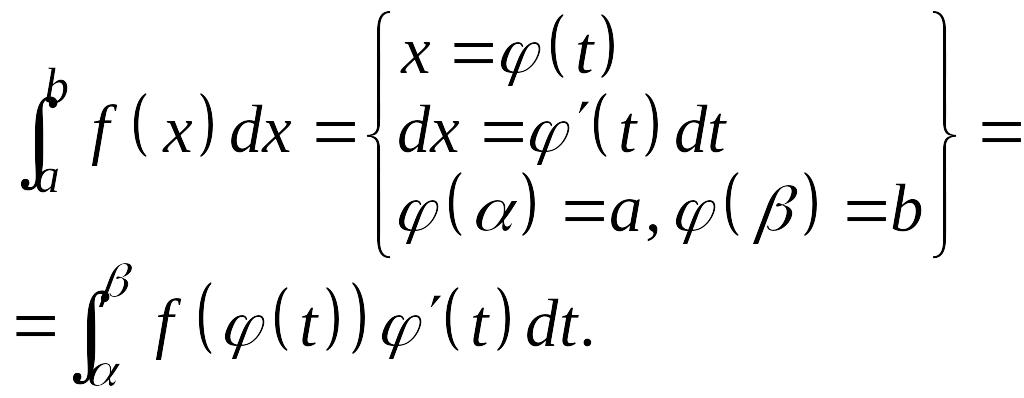
 бъём
тела вращения
бъём
тела вращения