2.4. Первообразная функция. Неопределенный интеграл и его свойства

Неопределённый интеграл

Опорный конспект

1. Понятие первообразной и неопределённый интеграл - совокупность первообразных, , .	3. Таблица интегралов , . . . . . . . . . . . . . .
2. Свойства неопределённого интеграла 10. . 20. . 30. . 40. . 50. . Частный случай: .
Методы интегрирования 1). Метод разложения (30, 40). 2). Метод замены переменной: . 3). Метод интегрирования по частям. . Применяется для: 1. , - многочлен, , . 2. , , . 3. .

Первообразная функция

Основная задача, изученная в теме «Производная», состояла в следующем: дана функция , требуется найти ее производную .

Рассмотрим теперь обратную задачу: дана функция , требуется найти такую функцию , для которой заданная функция является производной, то есть .

Решению этой важной задачи и посвящена изучаемая тема «Неопределенный интеграл».

Определение.

Функция называется первообразной для функции , если выполняется равенство

.

Например, для функции первообразной является функция , для – , для – , для – и т.д.

Изучая производную, мы видели, что каждая дифференцируемая функция имеет одну производную. Иначе обстоит дело с первообразными. Для функции первообразными являются функции , , , то есть все функции вида , где C – постоянная.

Таким образом, если функция имеет одну первообразную, то она имеет множество первообразных. Это множество описывают следующие две теоремы.

Теорема 1. Если функция является первообразной для функции , то функция , где C — произвольная постоянная, также будет первообразной для функции .

Неопределенный интеграл

Определение. Совокупность всех первообразных для функции называется неопределенным интегралом от функции и обозначается

.

Смысл этого обозначения будет раскрыт в теме «Определенный интеграл». Здесь – знак интеграла, – подынтегральная функция, – подынтегральное выражение, x — переменная интегрирования.

Итак, по определению , если , C – произвольная постоянная. Например,

, , .

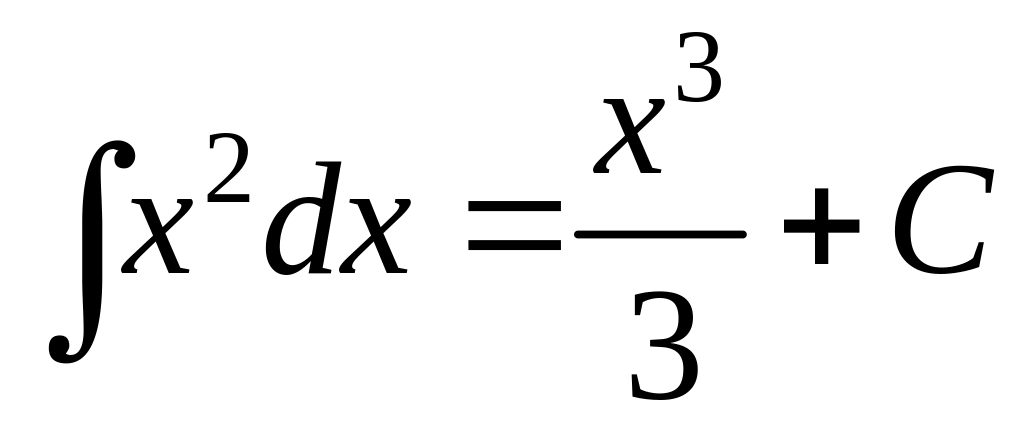Нахождение неопределенного интеграла для заданной функции называется интегрированием функции.

Геометрический смысл неопределенного интеграла — это совокупность кривых, получаемых путем сдвига одной из кривых параллельно самой себе вдоль оси 0y. Например, — совокупность парабол (рис.1).

Рис.1.

Свойства неопределенного интеграла

.

.

или ..

. (1.1)

.

Интегрирование функций. Таблица основных формул интегрирования

1. ,	6. ,
2. ,	7. ,
3. ,	8. ,
4. ,	9. ,
5. ,	10. .

Все формулы вытекают из таблицы производных.
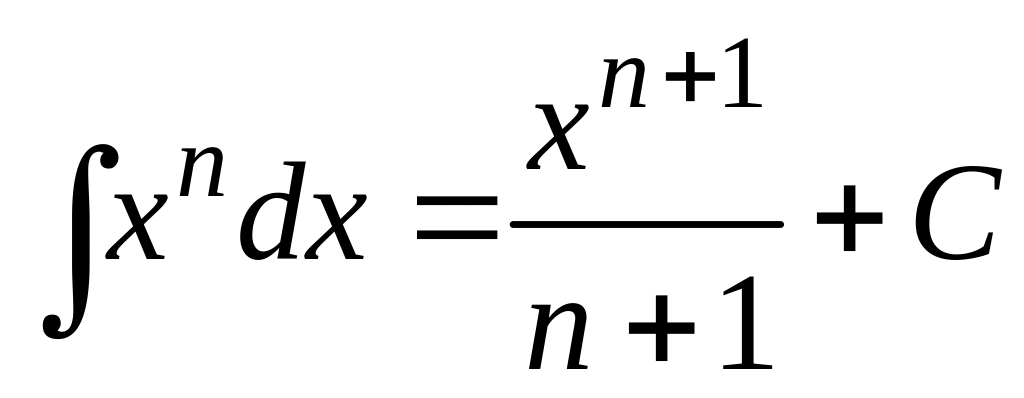
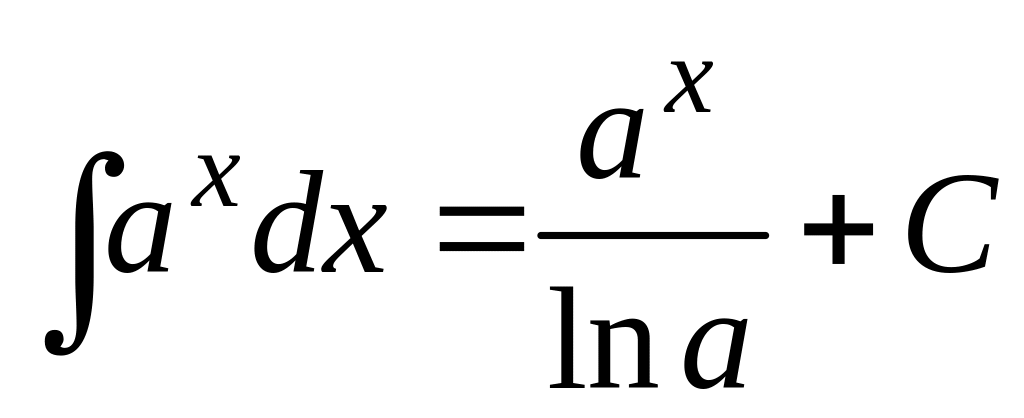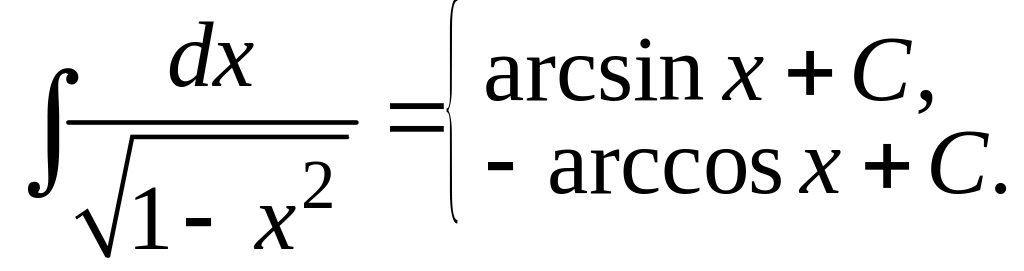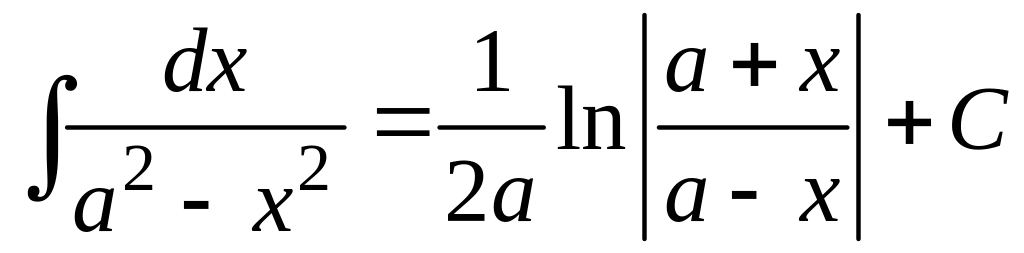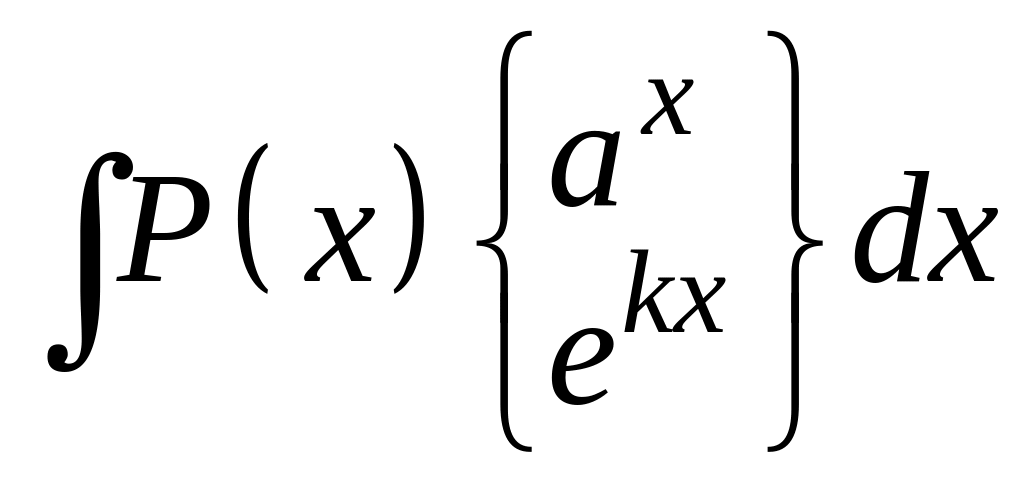
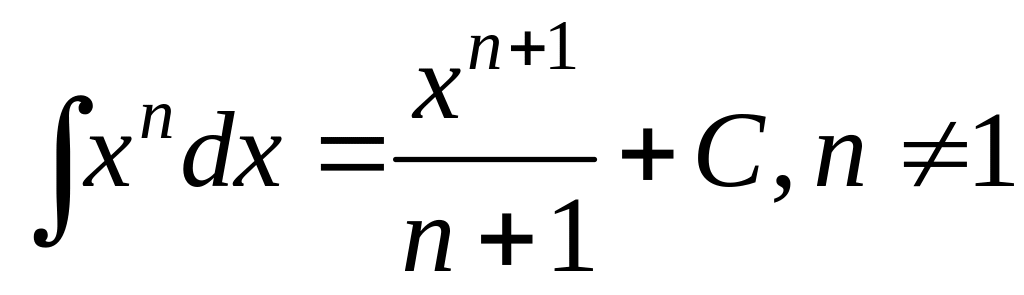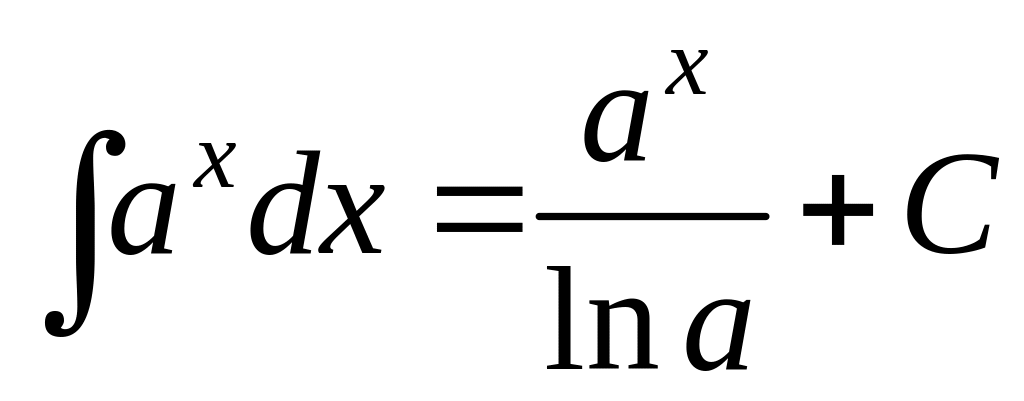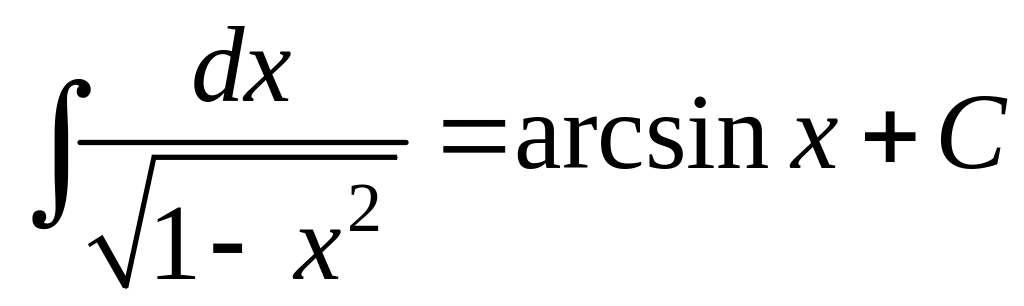