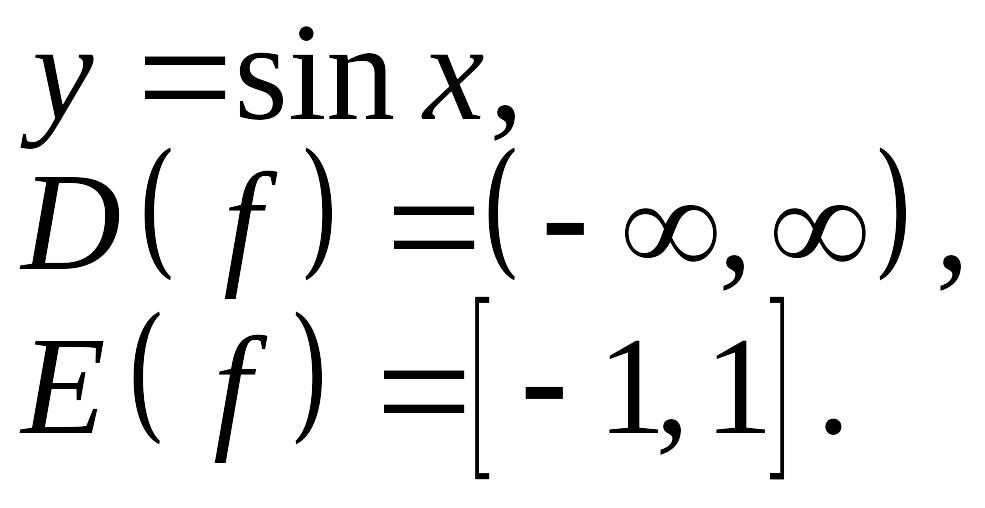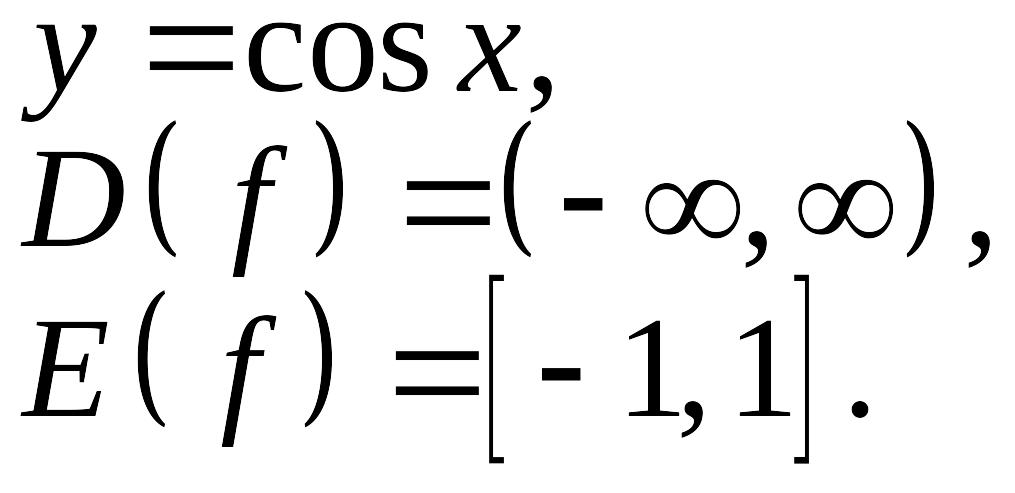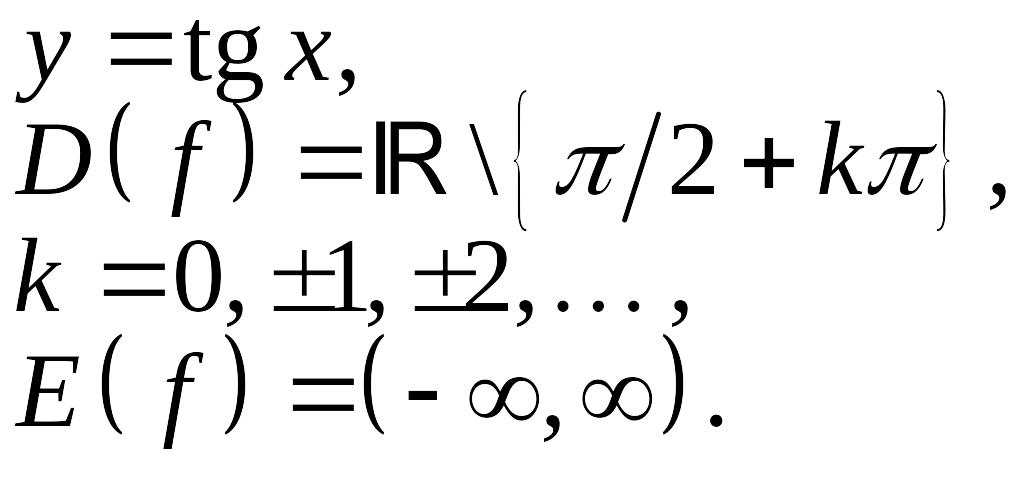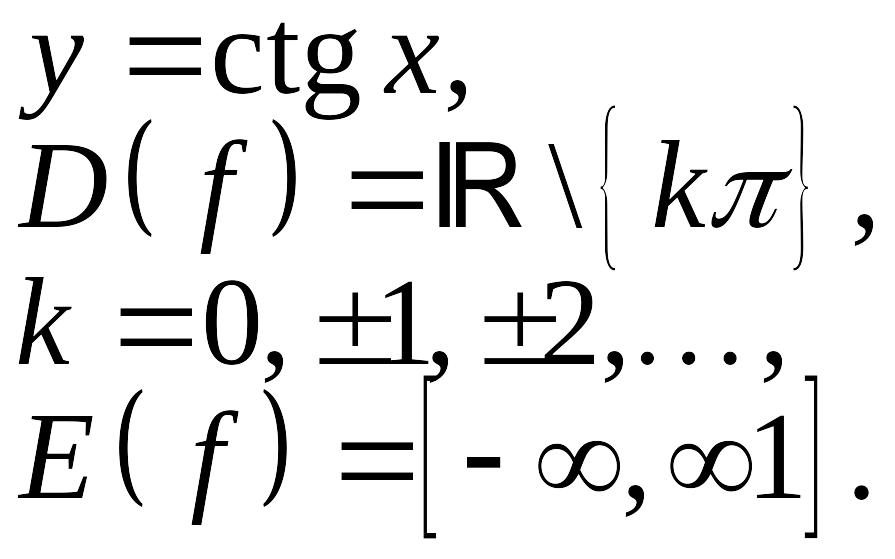- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
Элементы аналитической геометрии
Опорный конспект
1. Прямая на плоскости
|
.
|
3
|
4
1
2.
Гипербола : г. м. т.
3.
Парабола: г. м. т.
|
Тема2 Элементы математического анализа
2.1. Функции одной переменной. Элементарные функции (фоп)
Опорный конспект
1. Элементы теории множеств
|
2. Функции
|
|
3. Основные элементарные функции. Элементарные функции |
||
1
|
|
|
2 степенная,
|
||
3 показательная,
|
|
|
4.
логарифмическая,
|
|
|
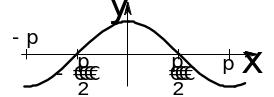
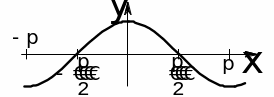
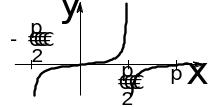
5.Тригонометрические:
|
|
|
|
|
|
|
||
|
||
Функции. Область определения. Способы задания
О:
Функцией
,
определённой на множестве
![]() и принимающей значения на множестве
и принимающей значения на множестве
![]() ,
называется такое правило соответствия
,
называется такое правило соответствия
![]() между этими множествами, при котором
для каждого
между этими множествами, при котором
для каждого
![]() существует единственный элемент
существует единственный элемент
![]() :
,
,
:
,
,
![]() :
:
![]() .
.
Множество
![]() - область определения функции;
- область значений функции;
- независимая переменная;
- зависимая переменная (функция.)
- область определения функции;
- область значений функции;
- независимая переменная;
- зависимая переменная (функция.)
На
языке геометрии функция
отображает множество
на множество
![]() ,
тогда
- образ
,
- прообраз
.
,
тогда
- образ
,
- прообраз
.
Пример.
Функция
![]() ,
,
![]() ,
,
![]() .
.
Если правило соответствия задаёт для каждого значения несколько или бесконечно много значений , то его называют многозначной функцией. При исследовании таких функций выбирают интервалы, где они однозначны.
Наиболее часто встречается три способа задания функции: аналитический, графический, табличный.
При
аналитическом способе функция задаётся
одной или несколькими формулами,
действующими на непересекающихся частях
области определения (например,
![]() ).
).
При
графическом способе функция задаётся
кривой (графиком) в плоскости
![]() ,
причём любая прямая, параллельная оси
,
причём любая прямая, параллельная оси
![]() ,
пересекает кривую не более чем в одной
точке.
,
пересекает кривую не более чем в одной
точке.
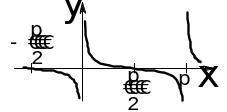
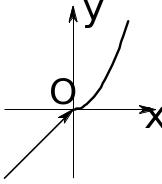
|
Рис. 4.1. |
 сли
функция задана аналитически, то её
график можно построить. Например, функция
сли
функция задана аналитически, то её
график можно построить. Например, функция
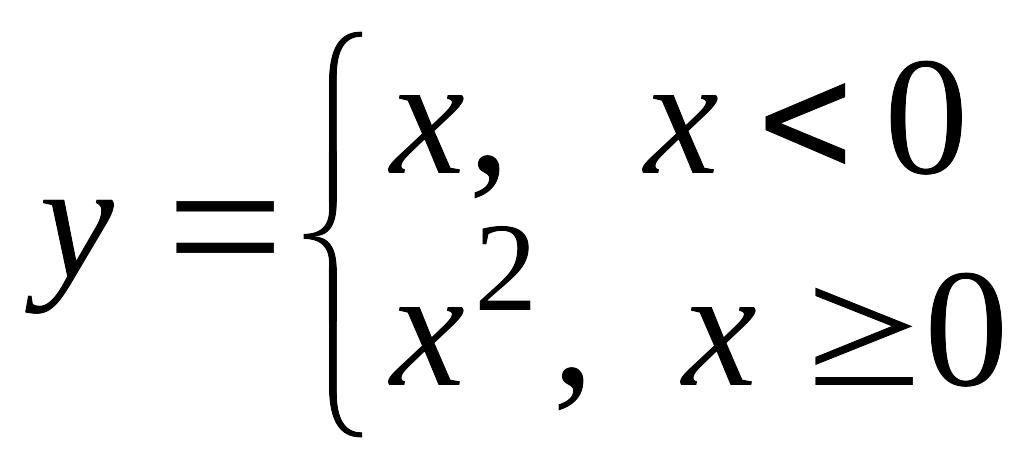 имеет график, изображённый на рис. 4.1.
Задание функции несколькими формулами
также называют логическим или
алгоритмическим способами. Например,
функция Дирихле:
имеет график, изображённый на рис. 4.1.
Задание функции несколькими формулами
также называют логическим или
алгоритмическим способами. Например,
функция Дирихле:
Некоторые свойства функций.
10.
Функция
называется возрастающей на
![]() ,
если большему значению аргумента
соответствует большее значение функции:
,
если большему значению аргумента
соответствует большее значение функции:
![]()
![]() ,
убывающей на
,
если
,
убывающей на
,
если
![]() .
Функция, только возрастающая или
убывающая на
называется монотонной.
.
Функция, только возрастающая или
убывающая на
называется монотонной.
Например,
![]() возрастает на
возрастает на
![]() и убывает на
и убывает на
![]() .
.
20.
Функция
![]() называется чётной, если
называется чётной, если
![]() ,
нечётной при
,
нечётной при
![]() .
.
Например,
- чётная,
![]() - нечётная функции.
- нечётная функции.
30.
Функция
![]() ,
называется периодической с периодом
,
называется периодической с периодом
![]() ,
если
,
если
![]() .
.
Например,
![]() - периодическая с периодом
- периодическая с периодом
![]() .
.
40.
Функция
![]() называется обратной к функции
,
устанавливающей взаимно-однозначное
соответствие между
и
называется обратной к функции
,
устанавливающей взаимно-однозначное
соответствие между
и
![]() ,
если
выражает то же соответствие, причём
,
если
выражает то же соответствие, причём
![]() ,
,
![]() .
.
Например,
![]() обратная к
обратная к
![]() при
при
![]() ,
,
![]() .
.
Основные элементарные функции. Элементарные функции
К основным элементарным функциям относятся:
постоянная
 ;
;степенная , , - задано;
показательная ,
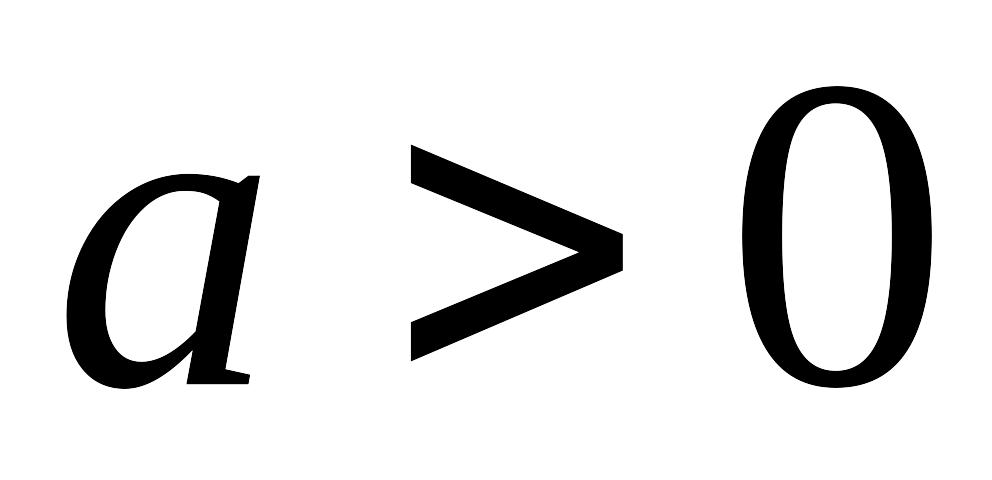 ,
,
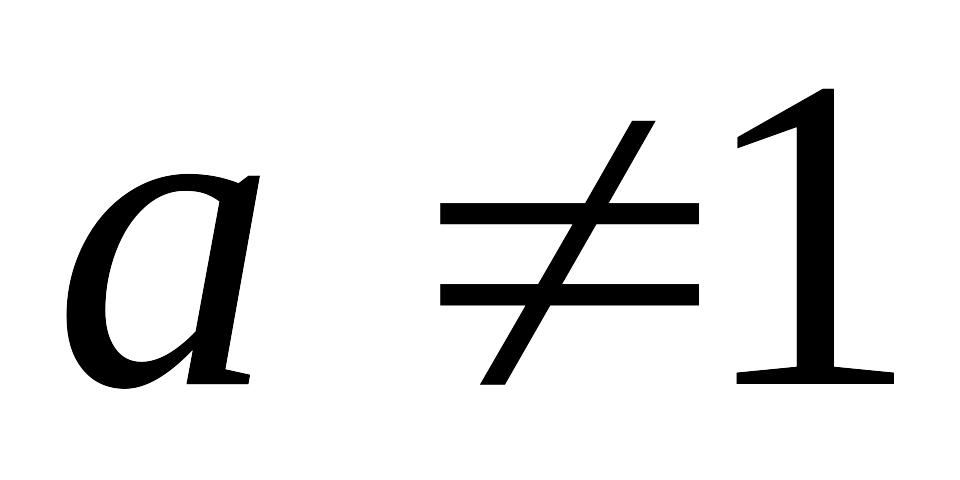 ;
;логарифмическая
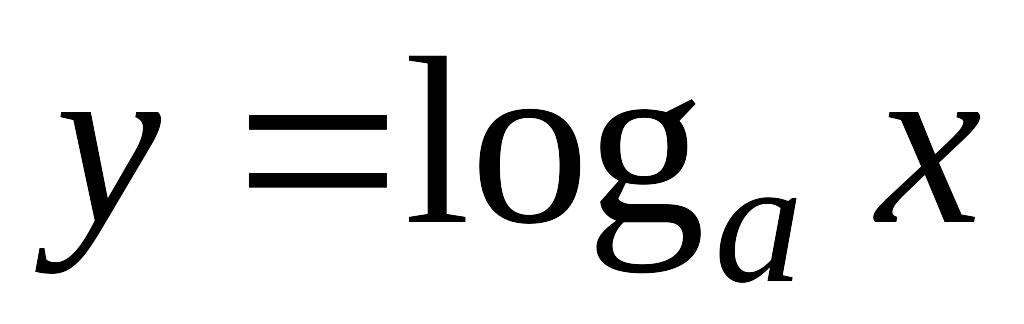 ,
,
(обратная к показательной);
,
,
(обратная к показательной);тригонометрические ,
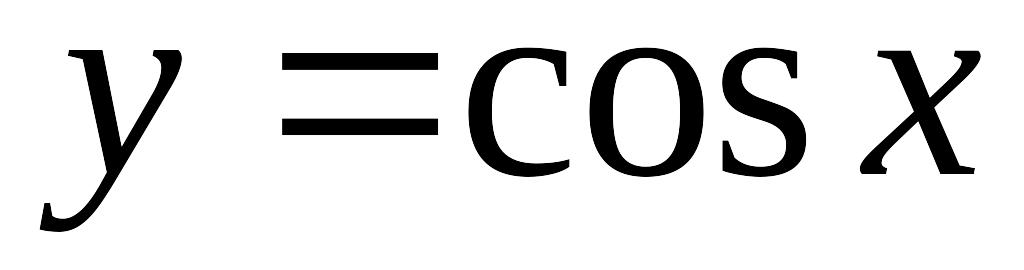 ,
,
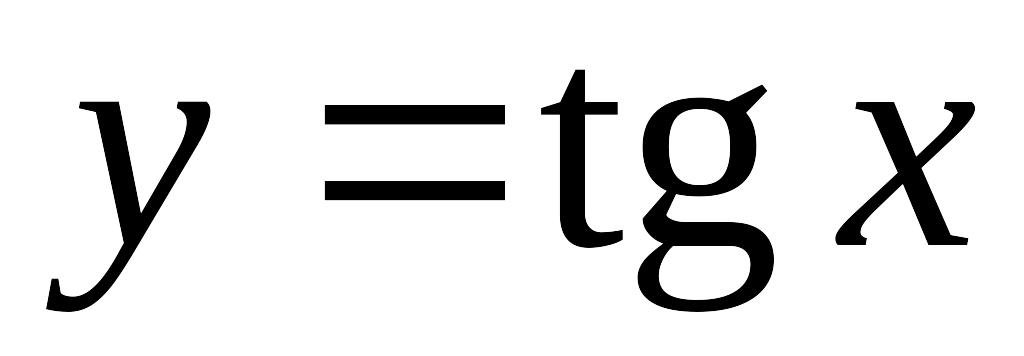 ,
,
 ;
;обратные тригонометрические
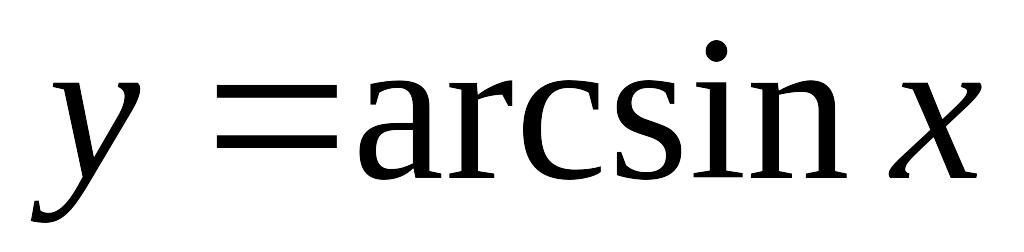 ,
,
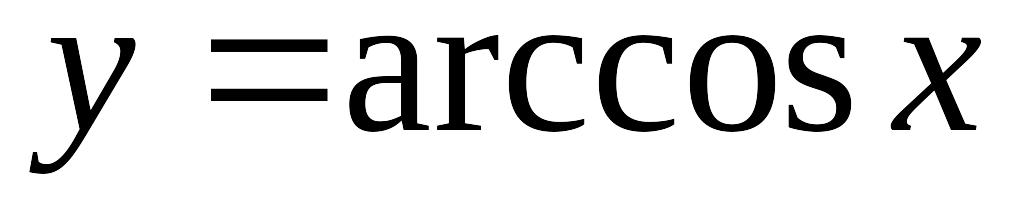 ,
,
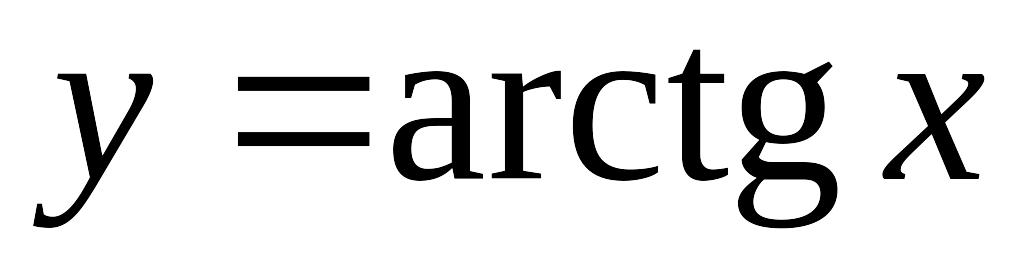 ,
,
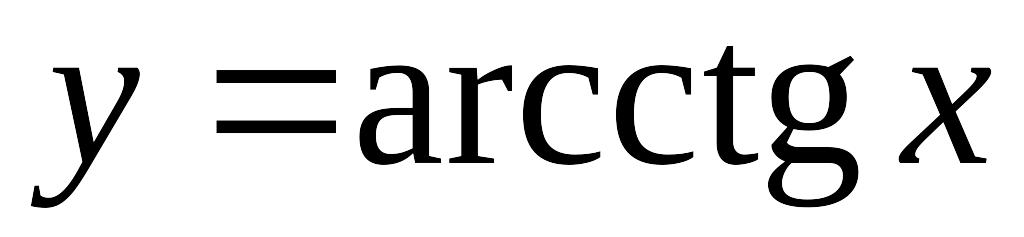 .
.
Области определения, значения этих функций и их графики приведены в опорном конспекте.
Обратные тригонометрические функции являются многозначными (бесконечно значными). При действиях с ними берутся их так называемые главные значения, заключённые в указанных в опорном конспекте № 4 интервалах.
О:
Сложной функцией
![]() (или суперпозицией) называется такая
функция, для которой:
(или суперпозицией) называется такая
функция, для которой:
![]() ,
,
,
,
![]() ,
,
![]() ,
,
,
,
![]() .
.
Например,
![]() ,
,
![]() .
.
Пользуясь понятием сложной функции, дадим определение элементарной функции.
О:
Элементарной функцией называется
функция, записанная одной формулой,
которая составлена из основных
элементарных функций с помощью символов
четырёх арифметических действий (![]() ,
,![]() ,
,
![]() ,
,
![]() )
и операции суперпозиции функций.
)
и операции суперпозиции функций.
Например,
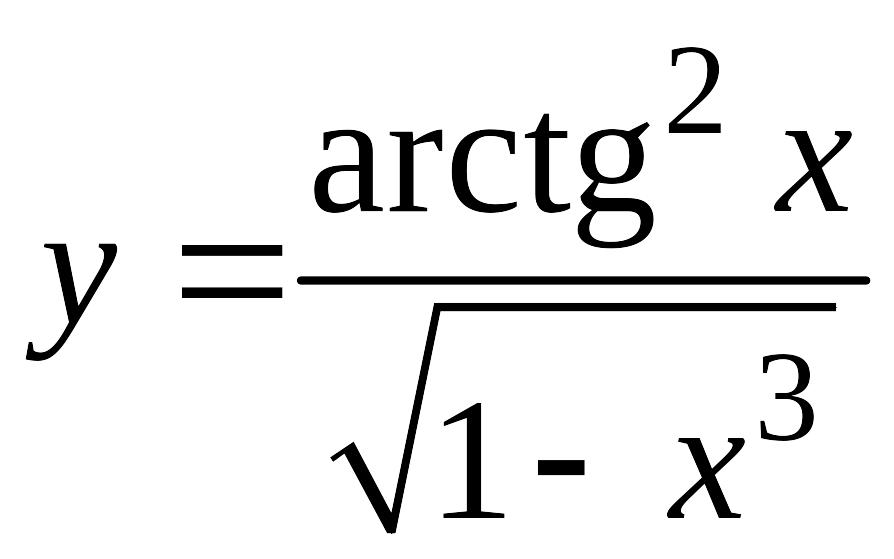 ,
,
![]() ,
,
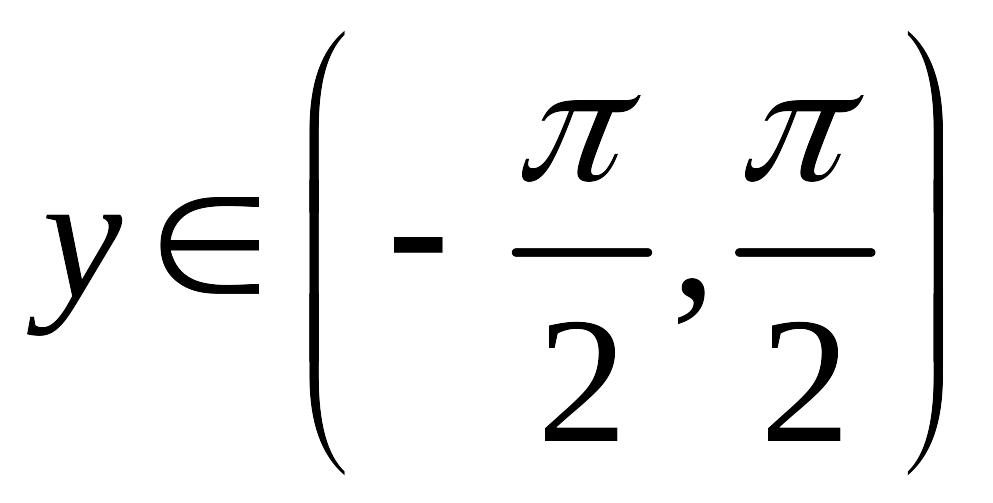 .
.

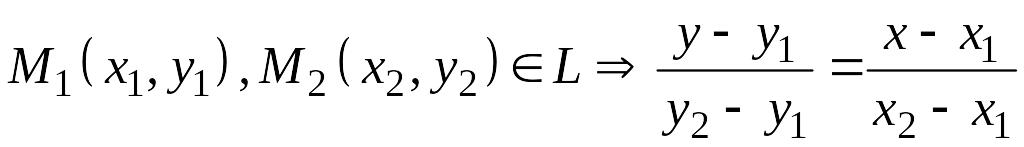
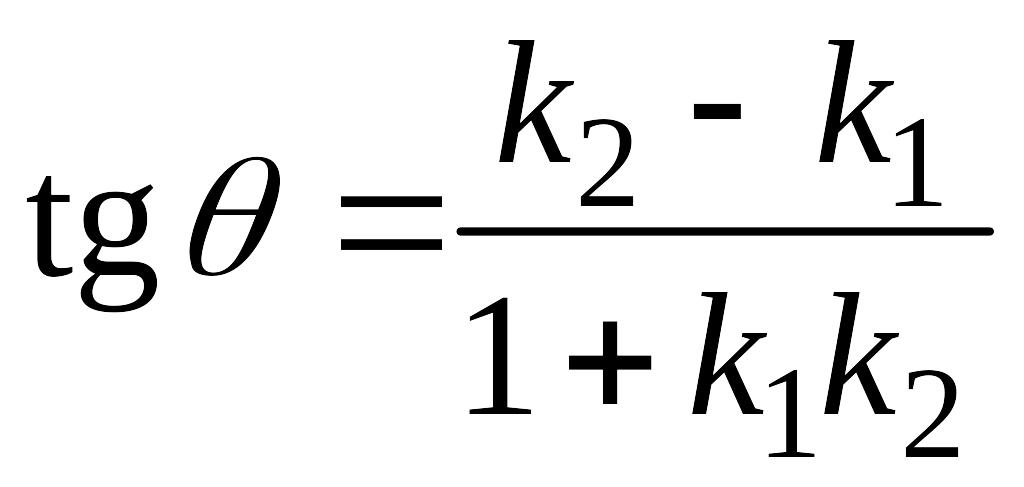
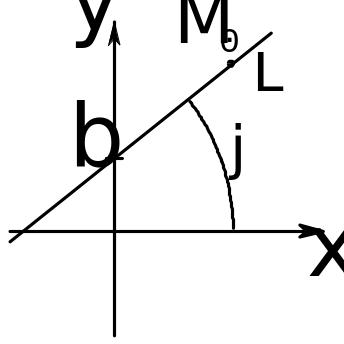 ,
,
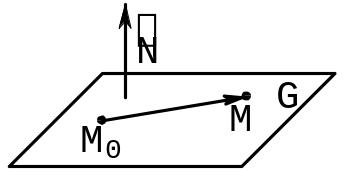 2.
Плоскость в пространстве
2.
Плоскость в пространстве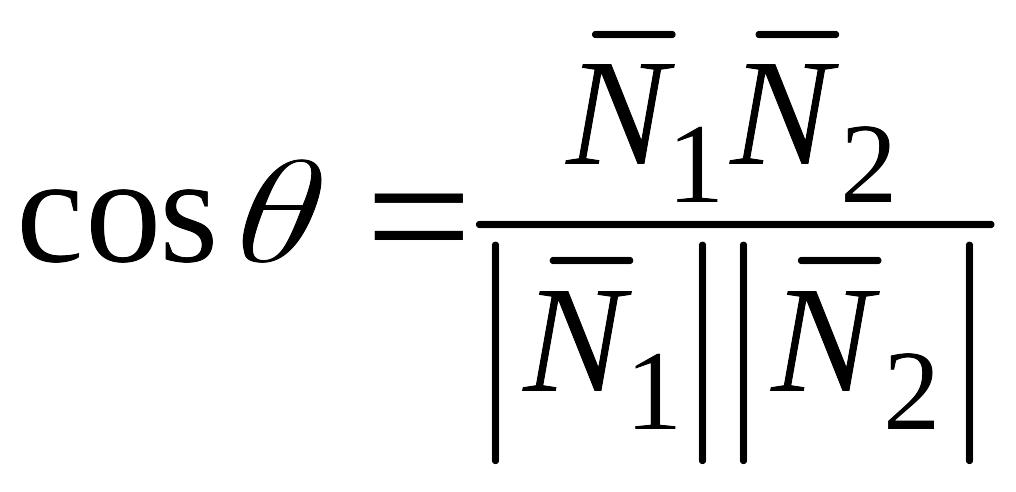 ,
- угол между
,
- угол между
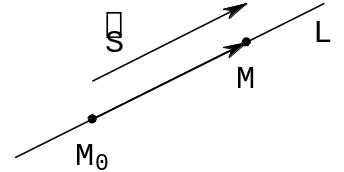 .
Прямая в пространстве
.
Прямая в пространстве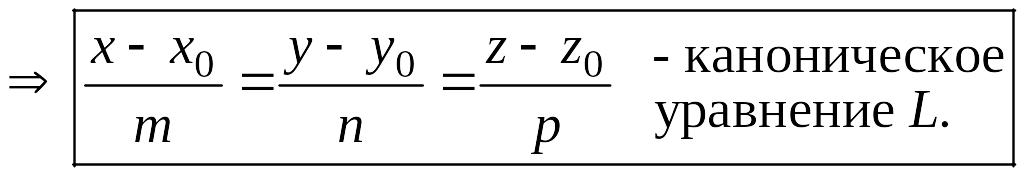
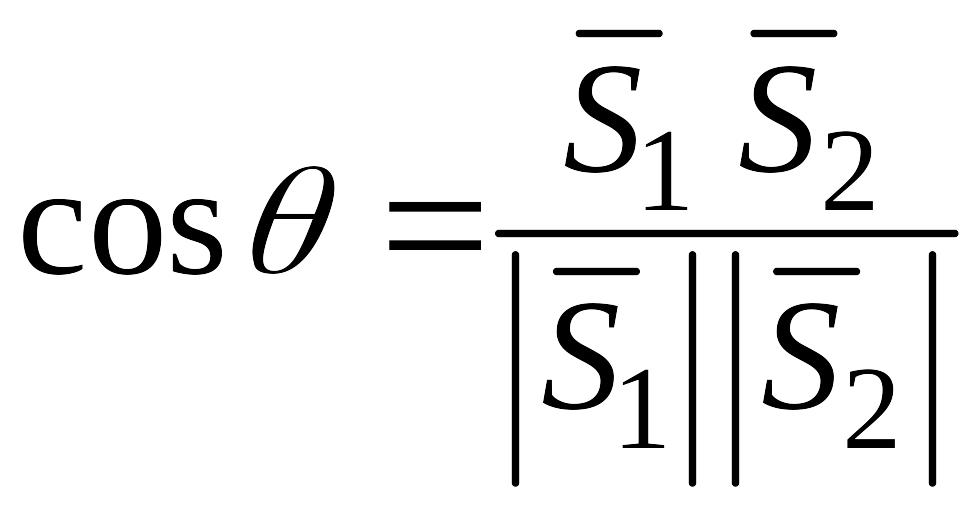 -
угол между
и
.
-
угол между
и
.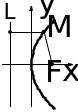 .
Кривые второго порядка на плоскости
.
Кривые второго порядка на плоскости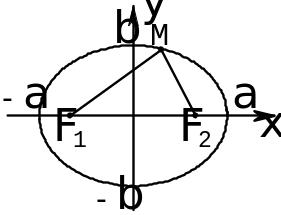 .
Эллипс: - г. м. т.
.
Эллипс: - г. м. т.
 ,
,
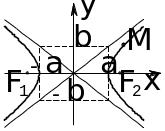 ,
,
- фокусы.
,
,
- фокусы. ,
,
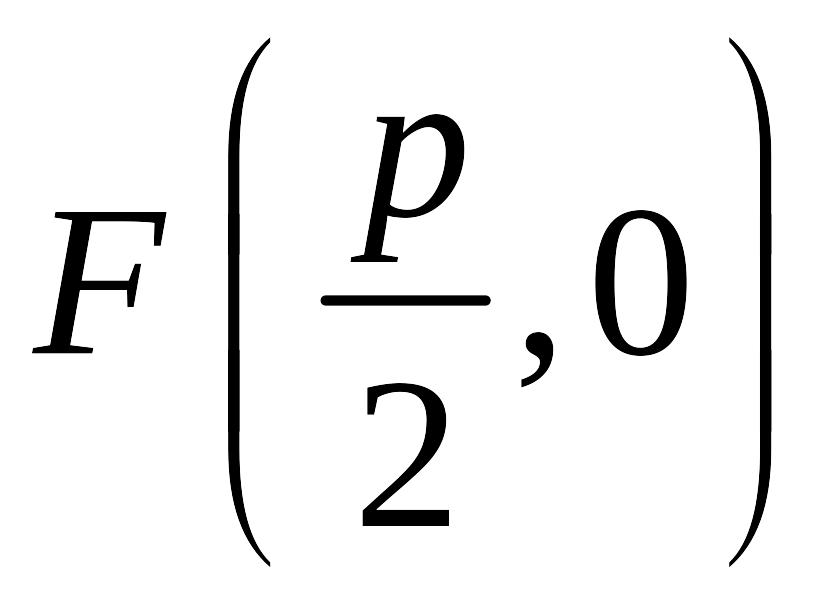 .
. .
.
 .
.
 .
.