- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
3.3.Элементы математической статистики
Опорный конспект
15.1. Основные понятия математической статистики.
О:
Выборка
О: Статистический ряд:
О: Статистический ряд по интервалам
-число значений СВ ,
О: Эмпирическая функция распределения:
|
15.2. Определение неизвестных параметров распределения
О:
Для выборки среднее арифметическое
О:
Доверительный интервал
Для
нормального распределения с параметрами
|
Основные понятия математической статистики Построение эмпирических законов распределения
Математическая статистика – наука о методах обработки экспериментальных данных, полученных при изучении закономерностей в случайных массовых явлениях. Способ статистической обработки, равно как и ценность её результатов полностью зависит от положенной в основу вероятностной модели, которая должна объяснить вероятностную структуру наблюдений.
Пусть
произведено
независимых экспериментов и получено
значений
![]() ,
,
![]() ,…,
,…,
![]() случайной величины
.
случайной величины
.
О:
Генеральной совокупностью называется
множество всех возможных значений
случайной величины
.
Выборкой объёма
![]() называется совокупность значений
,
полученных в результате
независимых экспериментов.
называется совокупность значений
,
полученных в результате
независимых экспериментов.
По исследованию выборки необходимо сделать правильный вывод о СВ . Например, по толщине покрытия 100 деталей из серии необходимо сделать вывод о качестве покрытия деталей. В этом случае классическую вероятность заменяют статистической.
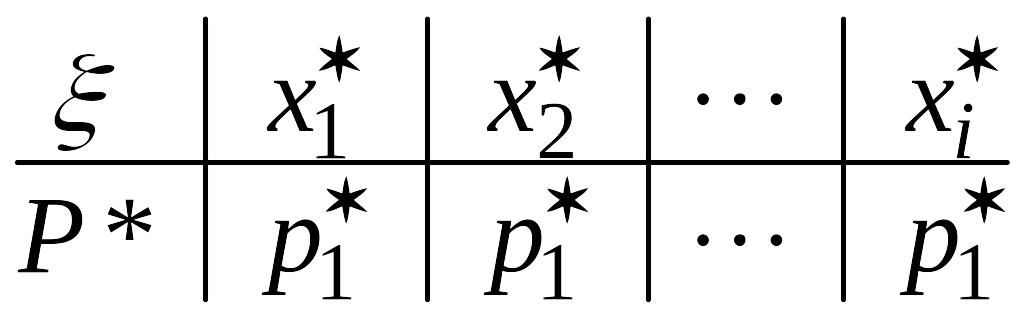
О:
Статистическим рядом называется таблица,
в которой записываются в упорядоченном
по возрастанию виде различные элементы
выборки
![]() ,
,
![]() ,
и относительные частоты
,
и относительные частоты
![]() (
(![]() - частота появления
- частота появления
![]() ):
):
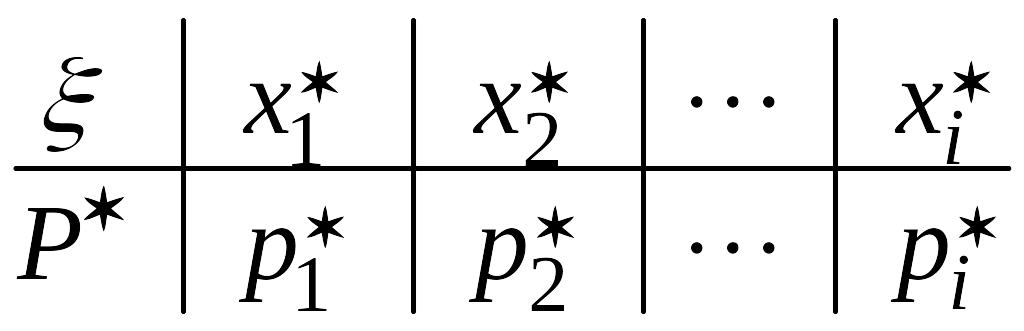 ,
,
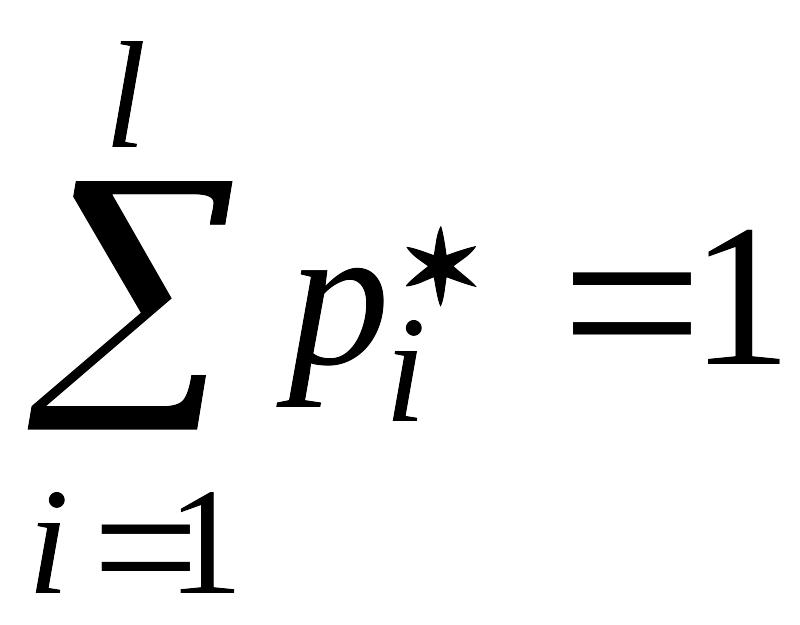 . (15.1)
. (15.1)
При большом числе измерений анализ такого материала затруднителен. Поэтому поступают следующим образом.
Составляется
статистический ряд по интервалам или
вариационный ряд. Весь интервал полученных
значений величины
разбивается на интервалы
![]() ,
,
![]() ,…,
,…,
![]() ,
подсчитываются относительные частоты
,
подсчитываются относительные частоты
![]() ,
где
- число значений величины
,
попавших в
,
и строится таблица:
,
где
- число значений величины
,
попавших в
,
и строится таблица:
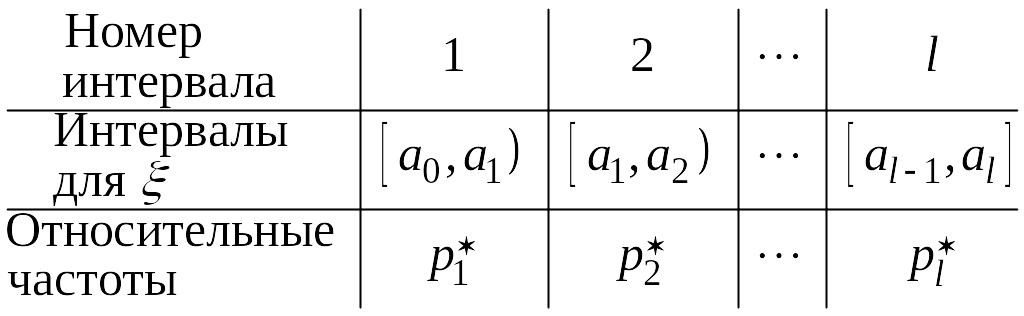 (15.2 )
(15.2 )
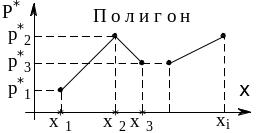
Графическими изображениями статистических рядов являются полигон и гистограмма.
Полигон
состоит из отрезков, соединяющих точки
![]() ,
,
где в случае ряда по интервалам
- срединное значение интервала
,
,
где в случае ряда по интервалам
- срединное значение интервала
![]() (рис. 15.1)
(рис. 15.1)
|
|
|
Рис 15.1. |
|
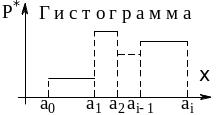
Рис. 15.2. |
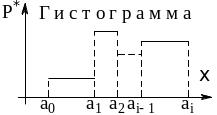
Гистограмма
служит для изображения интервального
статистического ряда (15.2). По оси
откладывают интервалы
,
варьирования СВ
и на этих отрезках строят прямоугольники
с высотами
![]() (рис. 15.2).
(рис. 15.2).
О:
Эмпирической функцией распределения
СВ
,
для которой составлен статистический
ряд (15.2), называется
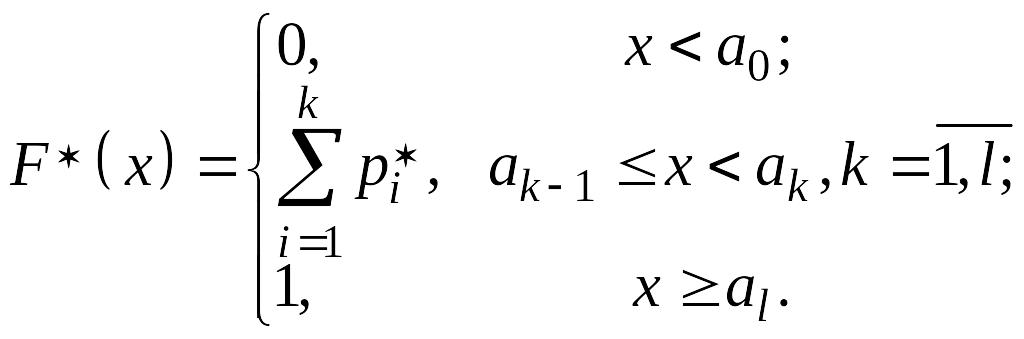
При
малых
![]() ,
и больших
функция
,
и больших
функция
![]() близка к теоретической функции
распределения
.
близка к теоретической функции
распределения
.
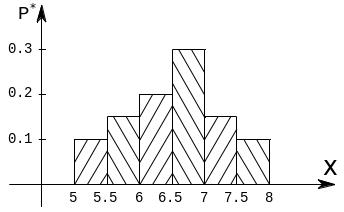
Пример. Толщина покрытия стального шарика в гальваническом производстве – случайная величина . Из партии отобрали случайным образом 20 шариков и измерили толщину покрытия в микрометрах.
: 6,99; 5,10; 5,61; 7,25; 5,45; 5,88; 7,92; 6,10; 5, 90; 6,22; 6,55; 6,34; 6,66; 6,48; 6,76; 6,87; 6,91; 7,05; 7,30; 7,70.
Построить статистический ряд по интервалам, гистограмму и график .
Решение.
Определяем
![]() ,
,
![]() ,
т.е. все значения выборки
,
т.е. все значения выборки
![]() .
Разобьём этот интервал на 6 частей с
.
Разобьём этот интервал на 6 частей с
![]() и построим статистический ряд.
и построим статистический ряд.
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
Интервал |
[5,0;5,5) |
[5,5;6,0) |
[6,0;6,5) |
[6,5;7,0) |
[7.0;7,5) |
[7,5;8] |
Относит.
частота
|
2/20 |
3/20 |
4/20 |
6/20 |
3/20 |
2/20 |
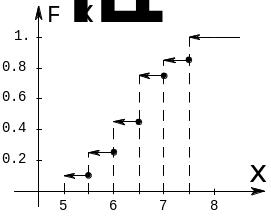
Гистограмма статистического ряда представлена на рис. 15.3. График эмпирической функции распределения изображён на рис. 15.4
|
|
Рис. 15.3. |
Рис.15.4 |
Определение неизвестных параметров распределения и выборочного коэффициента корреляции
Выборочные числовые характеристики. Оценки параметров
Для
выборки
![]() СВ
и для статистического ряда определяются
следующие числовые характеристики.
СВ
и для статистического ряда определяются
следующие числовые характеристики.
О:
Среднее арифметическое выборки
это
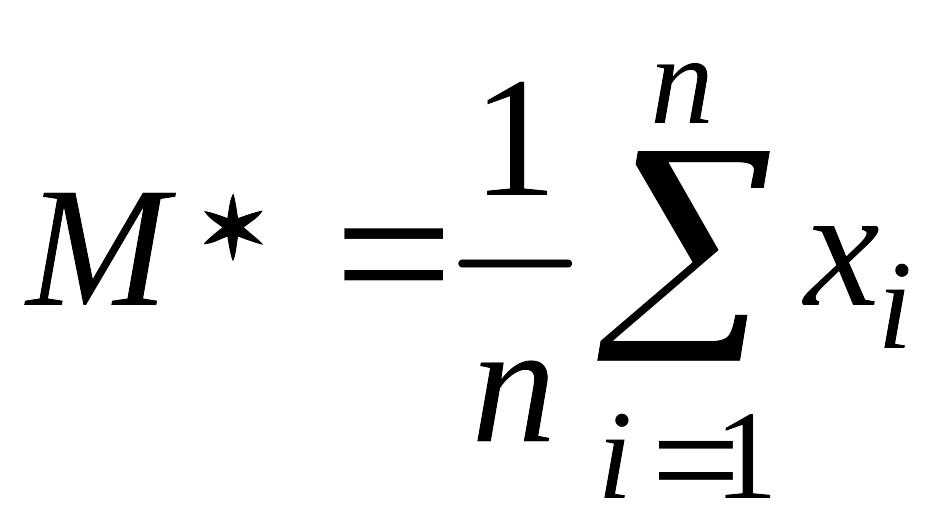 ,
,
среднее
арифметическое статистического ряда
(15.1):
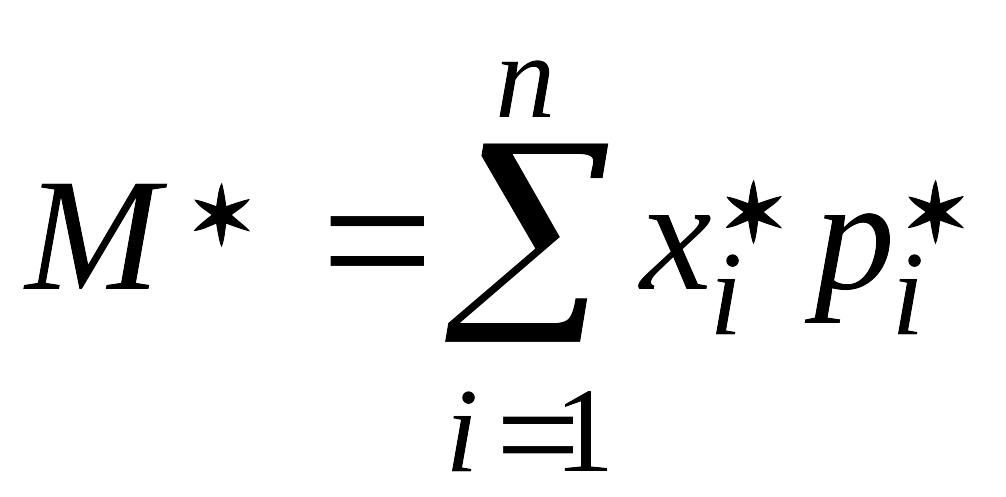 .
Дисперсия выборки
это
.
Дисперсия выборки
это
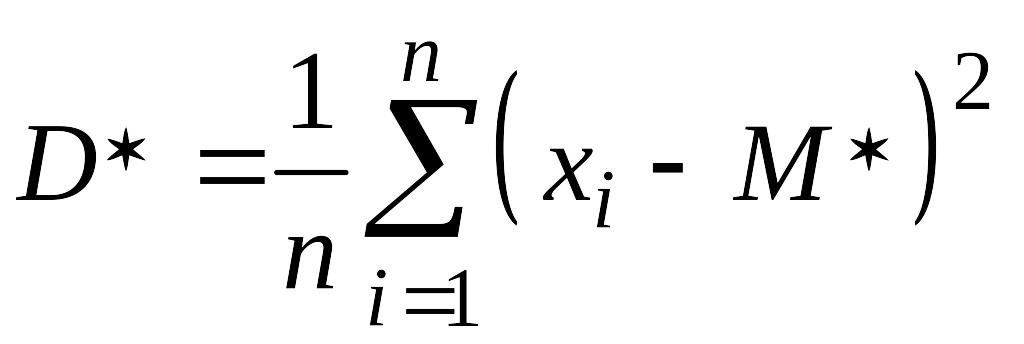 ,
,
дисперсия
статистического ряда (15.1) ‑
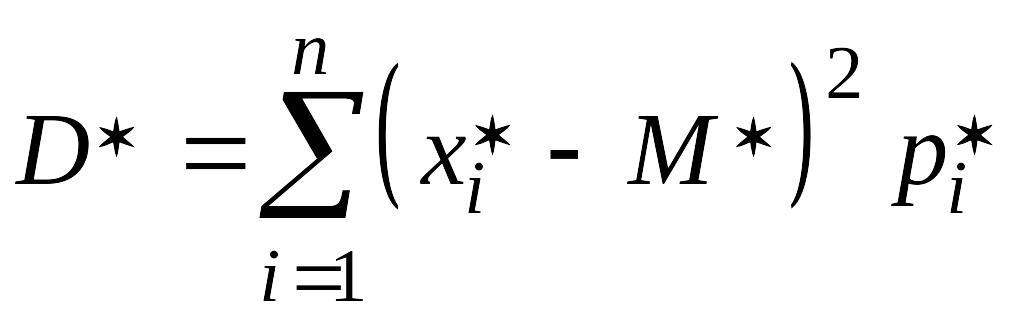 .
.
Среднее
квадратичное отклонение:
![]() .
.
Пусть
случайная величина с функцией распределения
![]() ,
где
- неизвестный параметр распределения,
т.е. неизвестная числовая характеристика
СВ
.
Например,
имеет нормальное распределение с
неизвестным параметром
,
где
- неизвестный параметр распределения,
т.е. неизвестная числовая характеристика
СВ
.
Например,
имеет нормальное распределение с
неизвестным параметром
![]() .
Рассмотрим
.
Рассмотрим
![]() выборок
выборок
![]() ,
,
![]() ,
этой СВ
.
Обозначим через
,
этой СВ
.
Обозначим через
![]() оценку величины
,
её можно представить как случайную
величину, зависящую от
оценку величины
,
её можно представить как случайную
величину, зависящую от
![]() ,
,
т.е.
,
,
т.е.
![]() .
Чтобы выбрать в некотором смысле лучшую
оценку
,
рассматриваются свойства оценок:
несмещённость, состоятельность,
эффективность.
.
Чтобы выбрать в некотором смысле лучшую
оценку
,
рассматриваются свойства оценок:
несмещённость, состоятельность,
эффективность.
О:
Оценка
параметра
называется несмещённой, если её
математическое ожидание
![]() ,
состоятельной, если
по вероятности сходится к
при
,
состоятельной, если
по вероятности сходится к
при
![]() ,
т.е.
,
т.е.
![]() .
Несмещённая оценка
называется эффективной, если её дисперсия
.
Несмещённая оценка
называется эффективной, если её дисперсия
![]() - наименьшая среди всех дисперсий,
вычисляемых для оценок
по выборкам одинакового объёма.
- наименьшая среди всех дисперсий,
вычисляемых для оценок
по выборкам одинакового объёма.
Т:
Среднее арифметическое
![]() выборки
СВ
,
имеющей математическое ожидание
и дисперсию
,
является несмещённой и состоятельной
оценкой математического ожидания. В
случае нормального распределения СВ
эта оценка является эффективной.
выборки
СВ
,
имеющей математическое ожидание
и дисперсию
,
является несмещённой и состоятельной
оценкой математического ожидания. В
случае нормального распределения СВ
эта оценка является эффективной.
Пример. Найти параметры распределения СВ в примере п. 15.1, если имеет нормальный закон распределения.
Решение.
Плотность вероятности для нормального
закона распределения
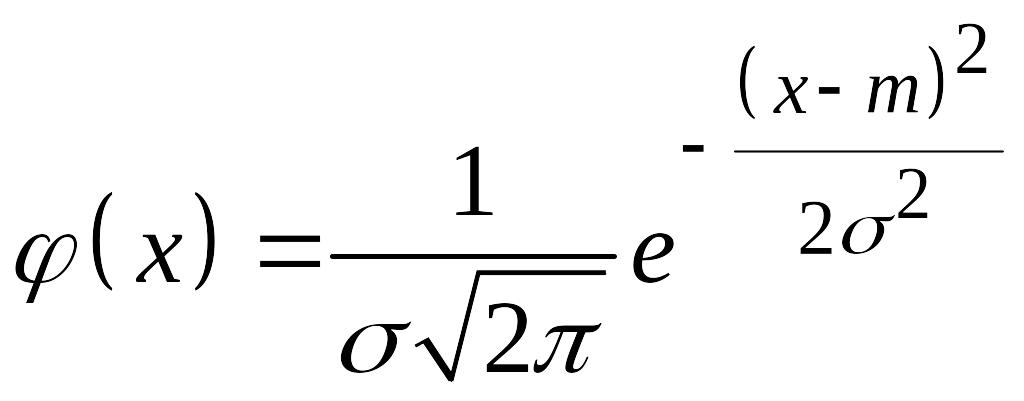 ,
неизвестные параметры -
,
.
Т.к.
,
неизвестные параметры -
,
.
Т.к.
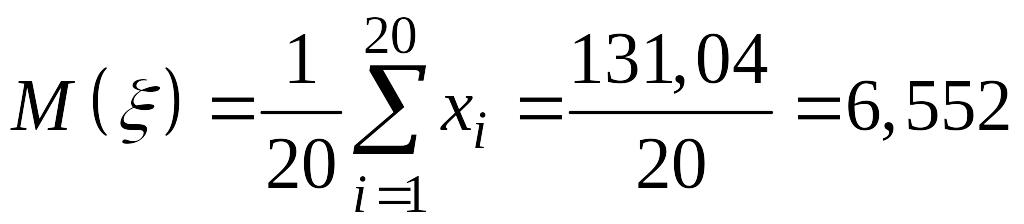 (мкм),
(мкм),
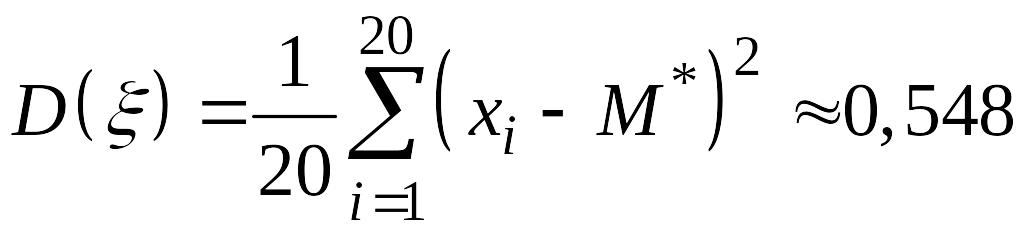 (мкм2),
то
(мкм2),
то
![]() ,
,
![]() .
.
Доверительные интервалы параметров
Рассмотренные
выше оценки параметров являются
точечными. При малом объёме выборки,
чтобы избежать грубых ошибок, вводят
интервальную оценку. Обозначим точность
оценки
параметра
через
![]() ,
т.е.
,
т.е.
![]() ,
а через
,
а через
![]() - вероятность
- вероятность
![]() ,
т.е.
,
т.е.
![]() .
Последнее условие означает, что интервал
.
Последнее условие означает, что интервал
![]() покрывает значение
с заданной вероятностью
.
Он называется доверительным интервалом,
- коэффициентом доверия. На практике
выбирают достаточно близким к 1.
покрывает значение
с заданной вероятностью
.
Он называется доверительным интервалом,
- коэффициентом доверия. На практике
выбирают достаточно близким к 1.
Величины , и объём выборки связаны между собой. Если определены две из них, то можно определить третью.
Пусть случайная величина имеет нормальное распределение с параметрами , .
В
качестве оценки
берётся
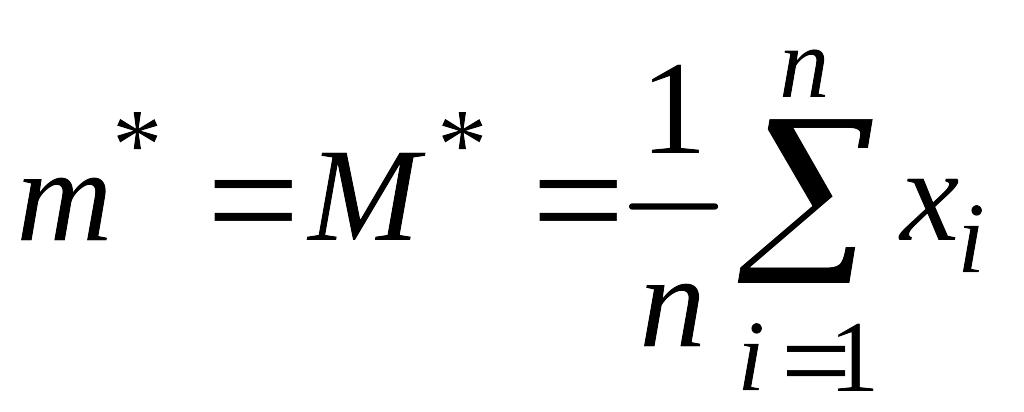 .
Все элементы
,
,
выборки случайные и имеют то же
распределение, что и
с параметрами
,
.
Все элементы
,
,
выборки случайные и имеют то же
распределение, что и
с параметрами
,
![]() .
Тогда по (15.6) в силу нечётности функции
Лапласа
.
Тогда по (15.6) в силу нечётности функции
Лапласа
![]() :
: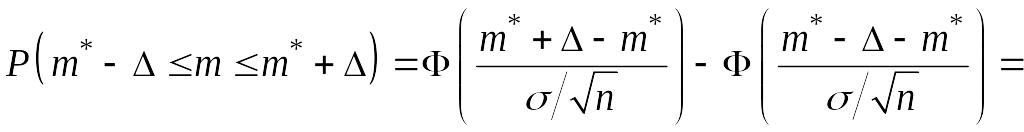
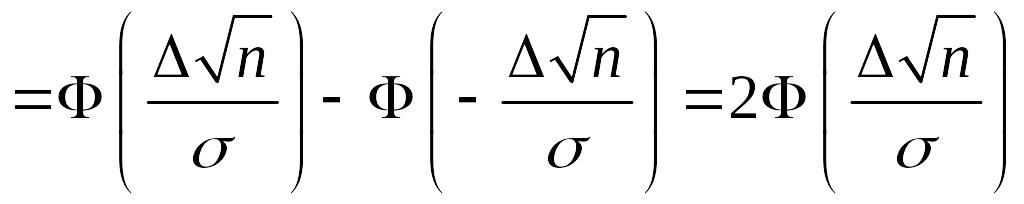 .
Обозначим
.
Обозначим
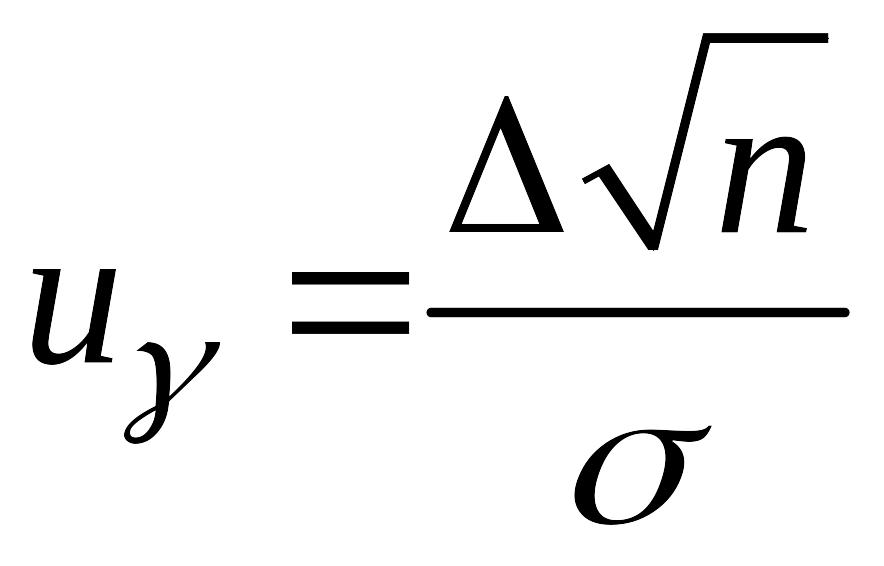 ,
тогда
,
тогда
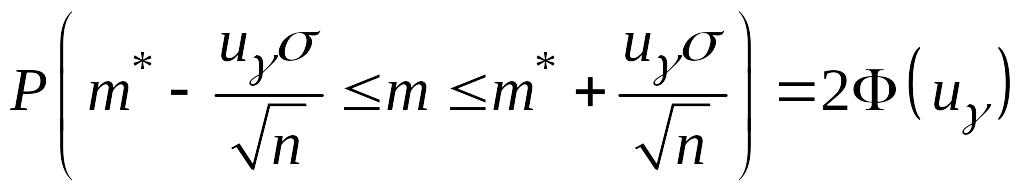 .
.
Если
задано, то
![]() находится по таблице функции Лапласа.
Интервал
находится по таблице функции Лапласа.
Интервал
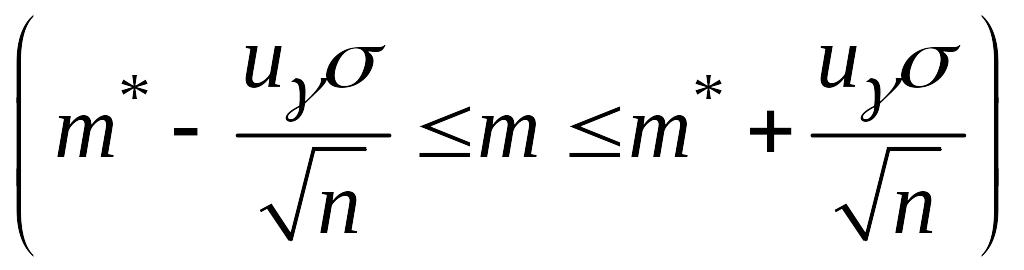 с вероятностью
покрывает значение
и является доверительным для
.
При этом предполагается, что
известно.
Если
заменить приближённым значением
с вероятностью
покрывает значение
и является доверительным для
.
При этом предполагается, что
известно.
Если
заменить приближённым значением
![]() ,
то коэффициент доверия
уменьшится.
,
то коэффициент доверия
уменьшится.
Пример.
Найти доверительный интервал с
коэффициентом доверия 0,95 для
![]() и
и
![]() .
.
Решение.
По таблице Лапласа
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
то имеем
,
то имеем
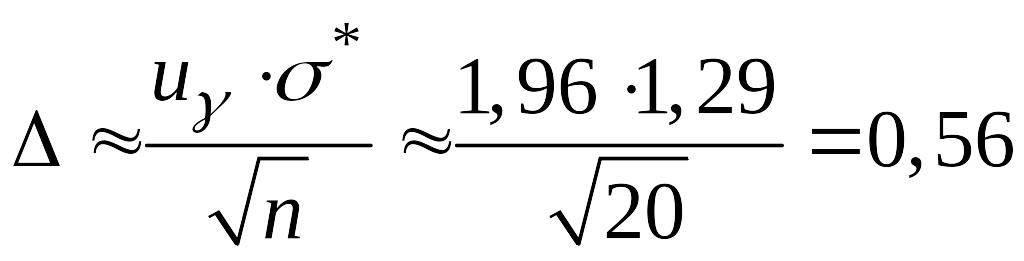 ,
доверительный интервал
,
доверительный интервал
![]() и
и
![]() .
.
Выборочный коэффициент корреляции
Пусть
проведено
независимых испытаний, в результате
которых получены выборочные значения
двумерной СВ
![]() :
(
:
(![]() ,
,
![]() ,
…,
,
…,
![]() ).
).
Аналогично
случаю одномерной СВ
определяются выборочные числовые
характеристики:
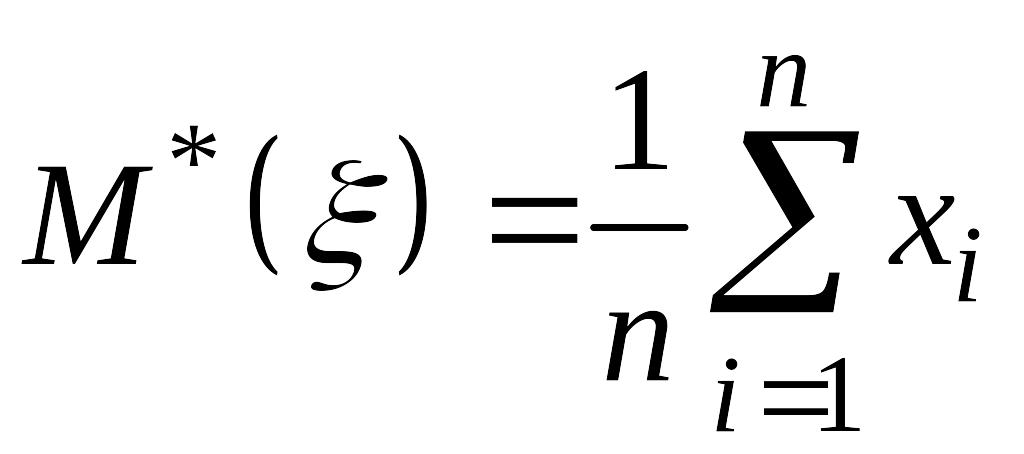 ,
,
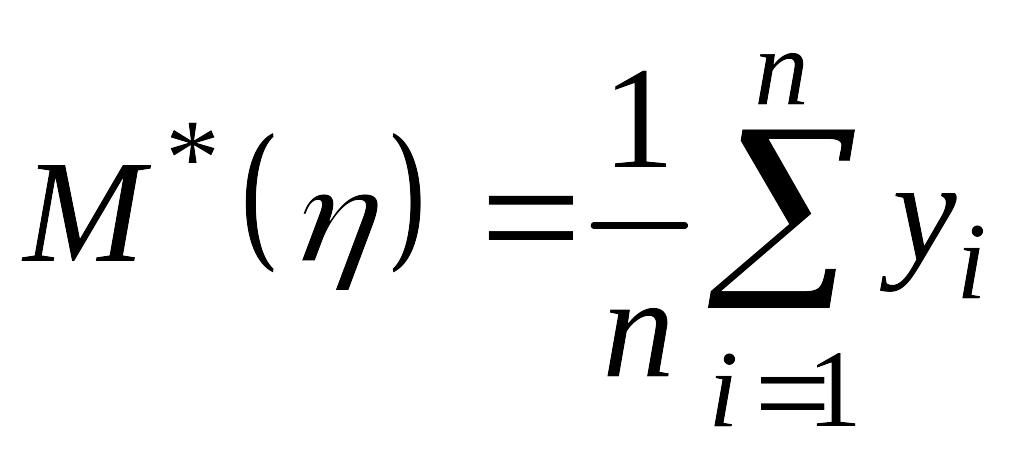 ,
,
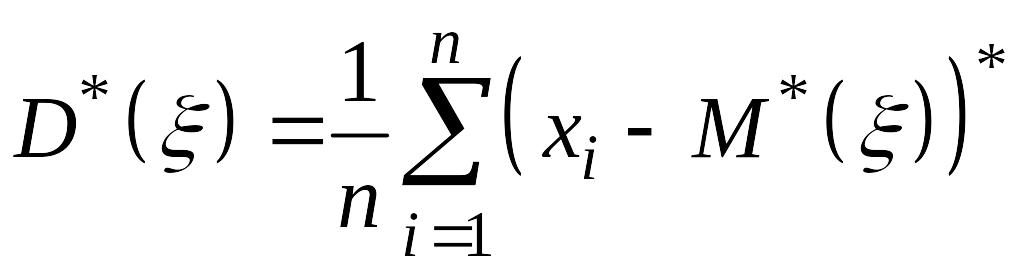 ,
,
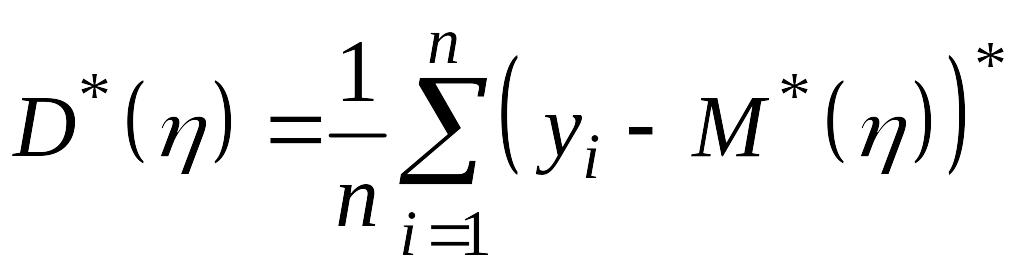 ,
,
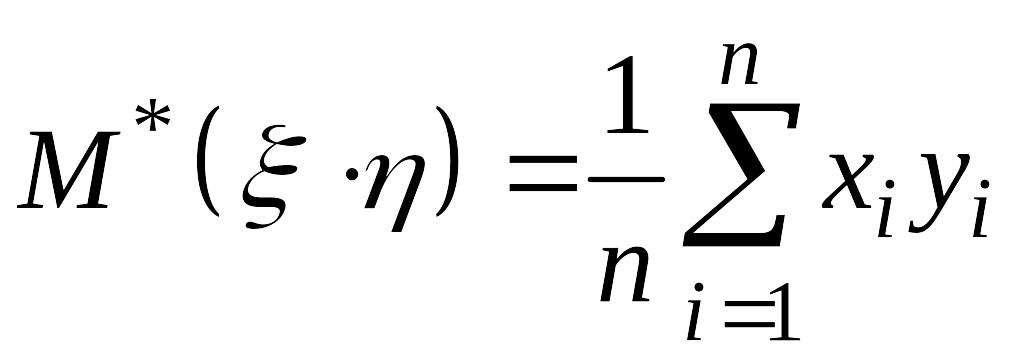 .
.
О:
Выборочным коэффициентом корреляции
СВ
называется
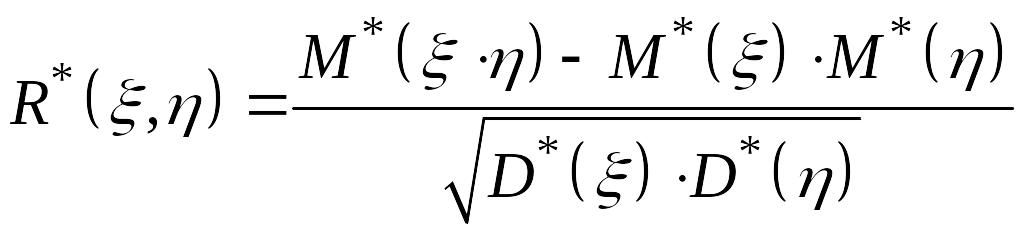 .
.
Пример.
Дана выборка СВ
:(2,2),
(4,5), (6,7), (8,10). Найти
![]() .
.
Решение.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
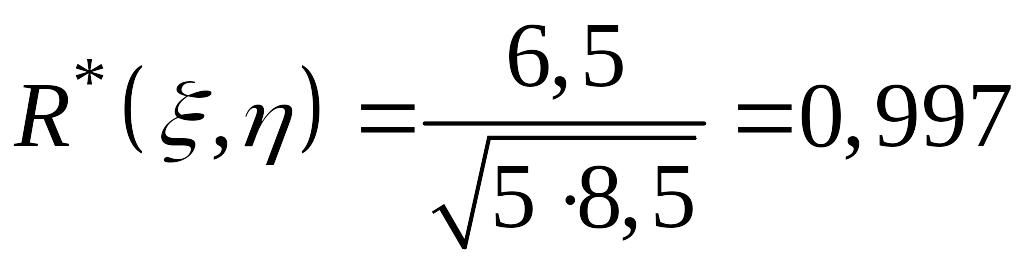 .
Коэффициент корреляции близок к 1, т.е.
зависимость между
,
.
Коэффициент корреляции близок к 1, т.е.
зависимость между
,
![]() близка к линейной.
близка к линейной.
Задача.
В таблице представлены данные по некоторой бригаде, где признак Х − трудовой стаж и Y − разряд.
Х |
8 |
9 |
5 |
7 |
5 |
7 |
9 |
5 |
6 |
5 |
Y |
5 |
6 |
2 |
4 |
6 |
5 |
7 |
6 |
4 |
3 |
1. Для признака Х построим вариационный ряд. Для этого расположим данные в порядке возрастания: 5, 5, 5, 5, 6, 7, 7, 8, 9, 9.
2. Полигоном называется ломанная линия, соединяющая точки (x1, n1), (x2, n2),.., (xr, nr), где ni − частота значения хi.
хi |
5 |
6 |
7 |
8 |
9 |
ni |
4 |
1 |
2 |
1 |
2 |
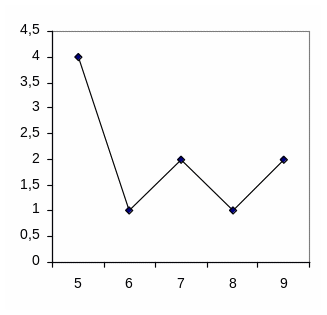
Рис.1 Полигон распределения
3.1 Мода распределения – это наиболее часто встречающееся значение ряда.
3.2 Выборочное среднее находится по формуле
![]() =
(х1+х2+х3+..
+хn)/n.
=
(х1+х2+х3+..
+хn)/n.
Средний
стаж равен
![]() (8+9+5+7+5+7+9+5+6+5)/10=6,6.
(8+9+5+7+5+7+9+5+6+5)/10=6,6.
Выборочная дисперсия распределения находится по формуле:
![]() .
.
В
нашем примере
![]() .
.
4.2
Оценка стандартного отклонения
определяется как корень квадратный из
выборочной дисперсии:
![]() .
.
4.3
Формула коэффициента вариации:
 .
.
Если Сv ≤ 10%, то варьирование считается слабым,
при 11% ≤ Сv ≤ 25% - средним, и значительным при Сv > 25%.
5. Доверительный интервал для оценки среднего значения нормального распределения при неизвестной дисперсии:
 ,
,
где
![]() - выборочная дисперсия, а значение
- выборочная дисперсия, а значение
![]() находят по таблице “Квантили распределения
Стьюдента”.
находят по таблице “Квантили распределения
Стьюдента”.
В таблице представлены данные о работниках бригады: разряд (Х) и стаж работы (Y, лет).
-
X
1
1
2
3
6
Y
1
2
3
4
5
Чаще всего, чем больше стаж работы, тем выше квалификация рабочего и, следовательно, выше его разряд. Поэтому в нашем примере стаж работы (Х) – независимая переменная, а разряд (Y) – зависимая от Х переменная.
Для построения корреляционного поля (диаграммы рассеивания) на координатную плоскость нанесем точки с координатами (1; 1), (1; 2), (2; 3), (3; 4), (6; 5) (рис.2). По конфигурации скопления точек мы можем предположить, что связь между стажем и разрядом есть, причем скорее всего эта связь линейная и положительная.
Найдем коэффициент линейной корреляции. Для удобства представим наши вычисления в виде следующей таблицы:
-
хi
yi
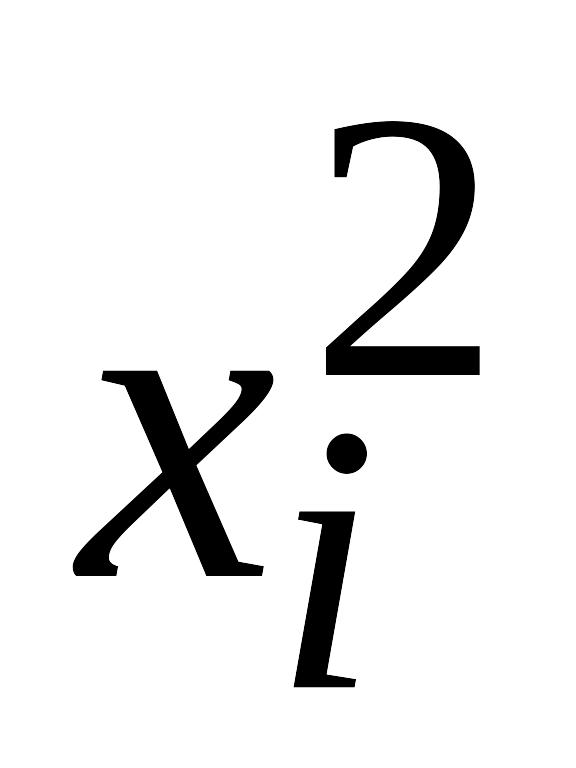
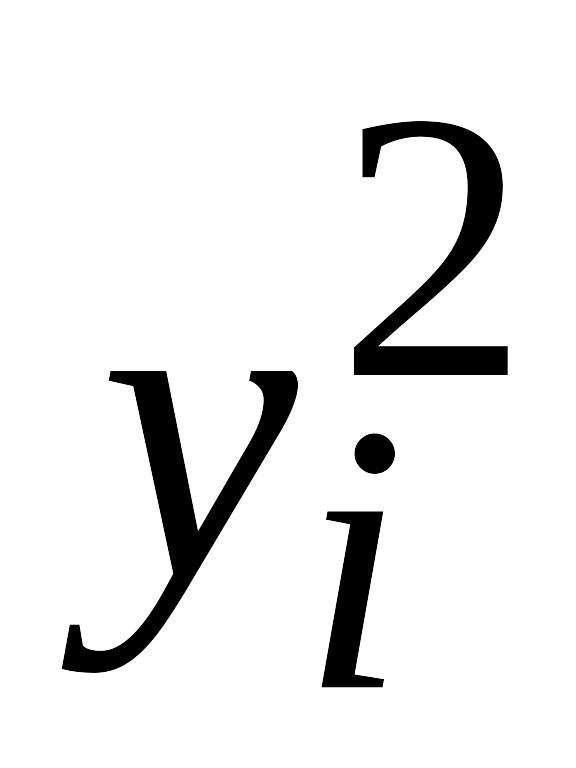
xiyi
1
1
1
1
1
1
2
1
4
2
2
3
4
9
6
3
4
9
16
12
6
5
36
25
30
∑ = 13
15
51
55
51
n = 5.
Выборочный коэффициент корреляции мы будем находить по следующей формуле:
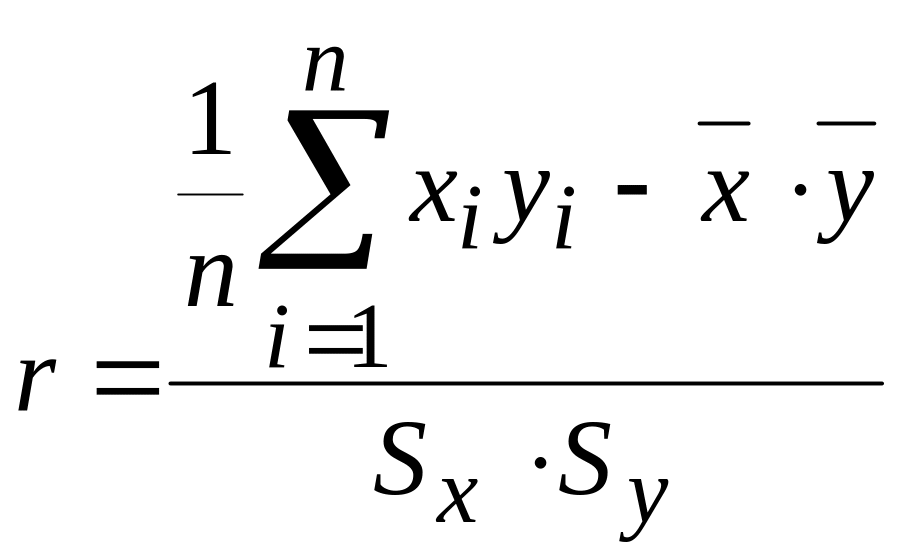 .
.
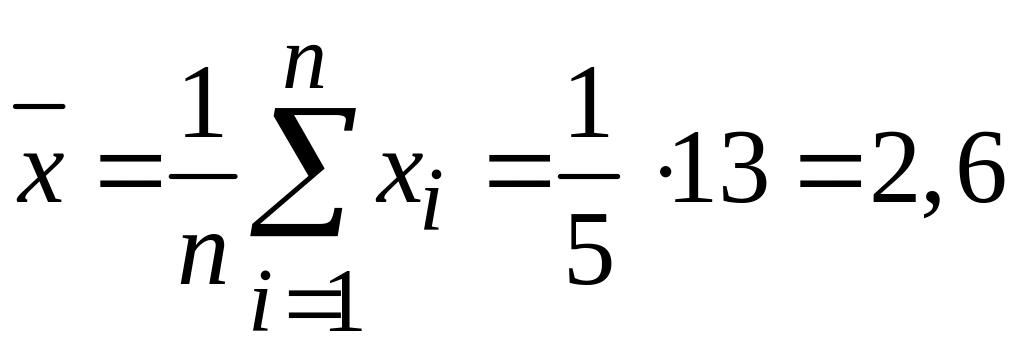 ,
,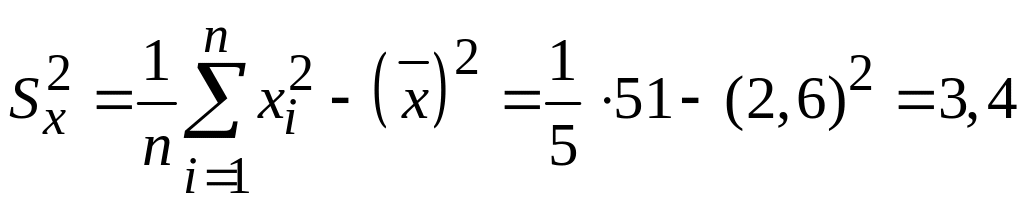 ,
,
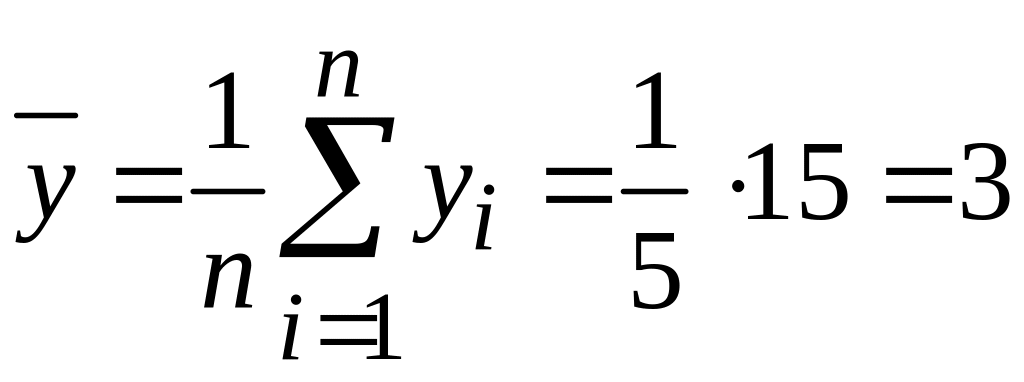 ,
,
 ,
,
 .
.
Полученное значение коэффициента r = 0,92 очень близко к 1, что указывает на сильную зависимость между стажем и разрядом рабочего.
Построим линию регрессии Y на Х.
![]() ,
,
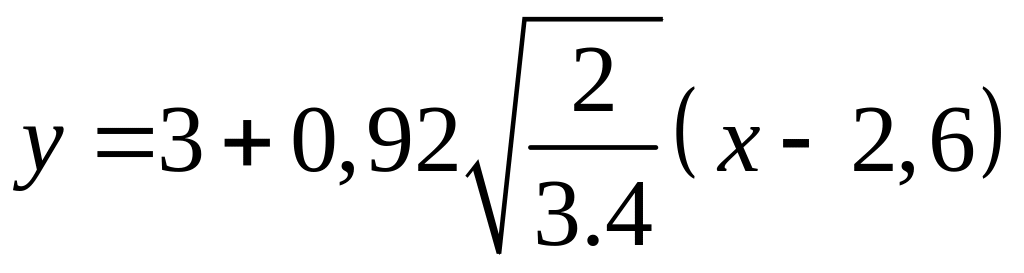 ,
,
y =0,7х + 1,17.
Получаем следующий график.
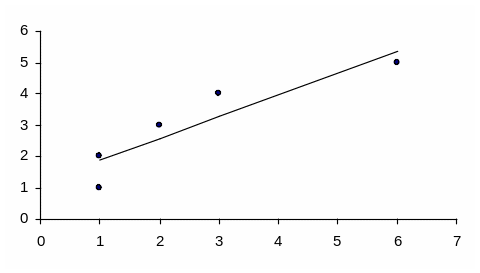
Рис.2

 ,
, попавших
в
попавших
в


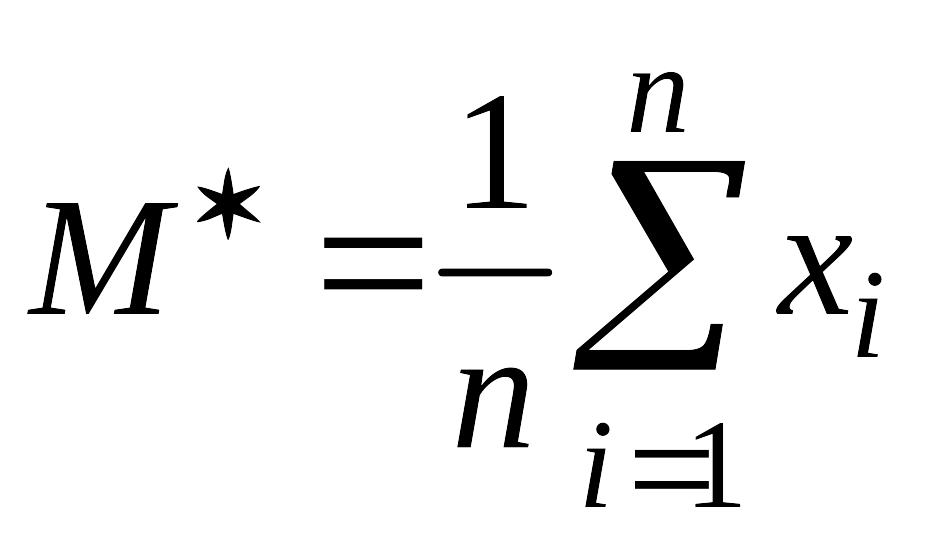 ,дисперсия
,дисперсия ,
,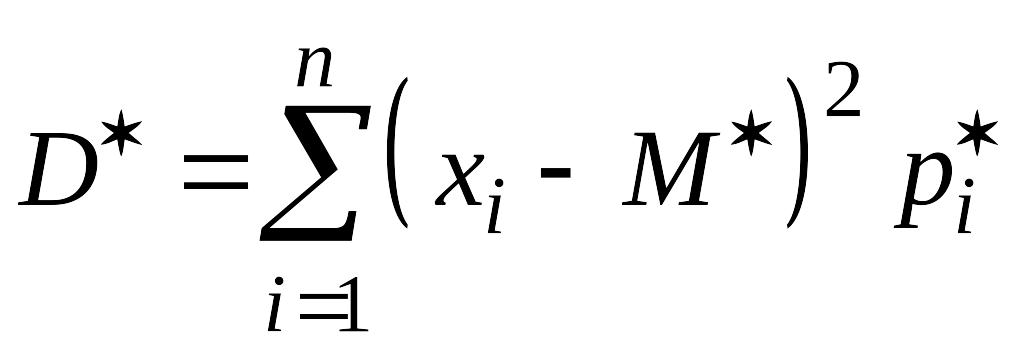 ;
;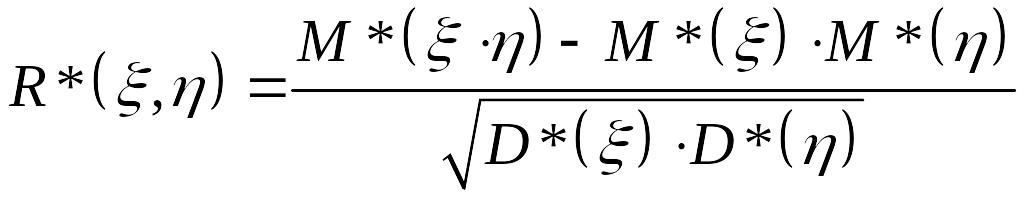 ,
,