- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
3.2. Случайные величины
Опорный конспект
14.1. Дискретные и непрерывные СВ. Закон распределения
О:
СВ
О:
Ряд распределения дискретной СВ –
табл.:
О:
Функция распределения СВ
О:
Плотность
распределения непр.СВ:
|
14.3. Примеры распределений дискретных и непрерывных СВ.
О:
Равномерное
распределение дискр. СВ
. О: Биноминальное распределение СВ
О:
Распределение Пуассона СВ
О:
Равномерное распределение непрерывной
СВ
О: Нормальное распределение СВ
|
14.2. Числовые характеристики СВ.
О:
Математич. ожидание дискретной СВ
|
Закон распределения
Пусть с некоторым экспериментом связано пространство элементарных событий .
О:
Случайной величиной (СВ)
![]() называется функция
называется функция
![]() .
.
Рассмотрим СВ двух видов: дискретные и непрерывные. Область возможных значений дискретной СВ состоит из конечного или счётного числа точек, а область возможных значений непрерывной СВ является некоторым интервалом.
Примеры.
1) Дискретная СВ
- число очков, выпавших при однократном
бросании кости:
![]() .
.
2)
Дискретная СВ – индикатор события
:
![]()
3) Непрерывная СВ – отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе.
О: Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими этим значениям вероятностями.
Для дискретной СВ закон распределения может быть задан в виде ряда распределения или в виде функции распределения, для непрерывной СВ ‑ в виде функции распределения и плотности распределения.
Обозначим
![]() вероятность того, что
примет значение
вероятность того, что
примет значение
![]() .
.
О:
Рядом распределения дискретной СВ
называется закон распределения, заданный
в виде таблицы значений
![]() и вероятностей
и вероятностей
![]() ;
;
![]() :
:
![]() .
.
Графическое изображение, представленное на рис. 14.1, называется многоугольником распределения.
|
Рис. 14.1. |
Ряд
распределения
![]()
О:
Функцией распределения вероятностей
СВ
называется
![]() ,
,
т.е. значение функции в т.
равно вероятности того, что СВ
,
,
т.е. значение функции в т.
равно вероятности того, что СВ
![]() .
.
Если
для дискретной СВ
![]() построен ряд распределения,
построен ряд распределения,
![]() то функция распределения имеет вид:
то функция распределения имеет вид:
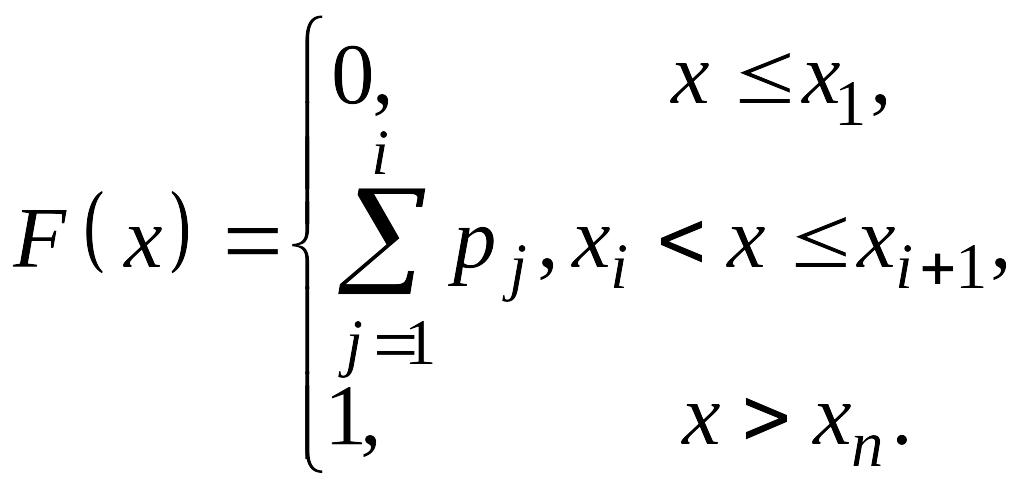
![]() её
график – ступенчатая функция (рис.14.2).
её
график – ступенчатая функция (рис.14.2).
|
Рис. 14.2. |
 ример.
Бросается игральная кость
ример.
Бросается игральная кость
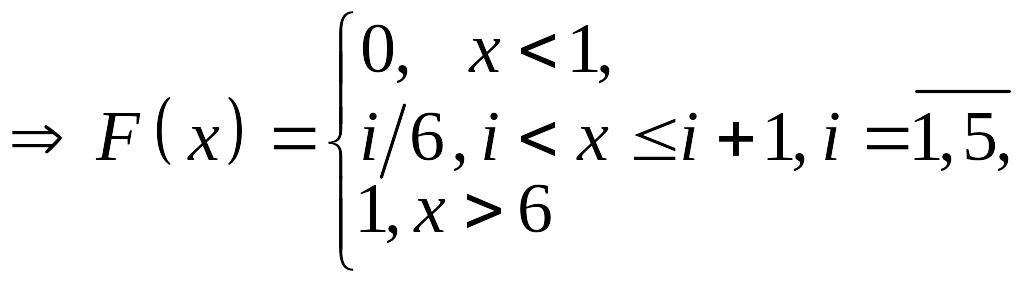 .
.
Функция распределения обладает следующими свойствами:
10.
![]() - неубывающая функция;
- неубывающая функция;
20.
![]() .
.
Г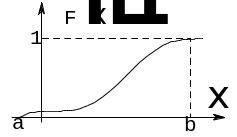 рафик
непрерывной СВ имеет вид кривой,
изображённой на рис. 14.3.
рафик
непрерывной СВ имеет вид кривой,
изображённой на рис. 14.3.
|
Рис. 14.3. |
О: Плотностью распределения вероятностей (плотностью распределения) для функции распределения непрерывной СВ называется функция такая, что .
Так
как
неубывающая функция, то
![]() .
.
На основании формулы Ньютона-Лейбница:
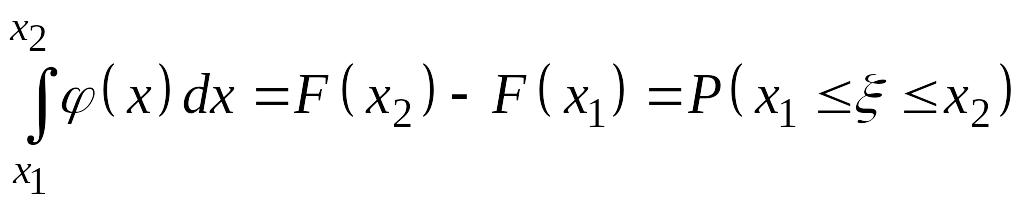 . (14.1)
. (14.1)
Используя определение несобственного интеграла с бесконечными пределами интегрирования, функцию можно записать через плотность распределения :
 .
.
Формула
справедлива и в случае конечного числа
точек разрыва 1 рода функции
.
Из достоверности события
![]() имеем
имеем
 .
.
Числовые характеристики случайных величин
Для характеристики среднего значения СВ вводится математическое ожидание.
О:
Математическим ожиданием дискретной
СВ
с законом распределения
![]() называется
называется
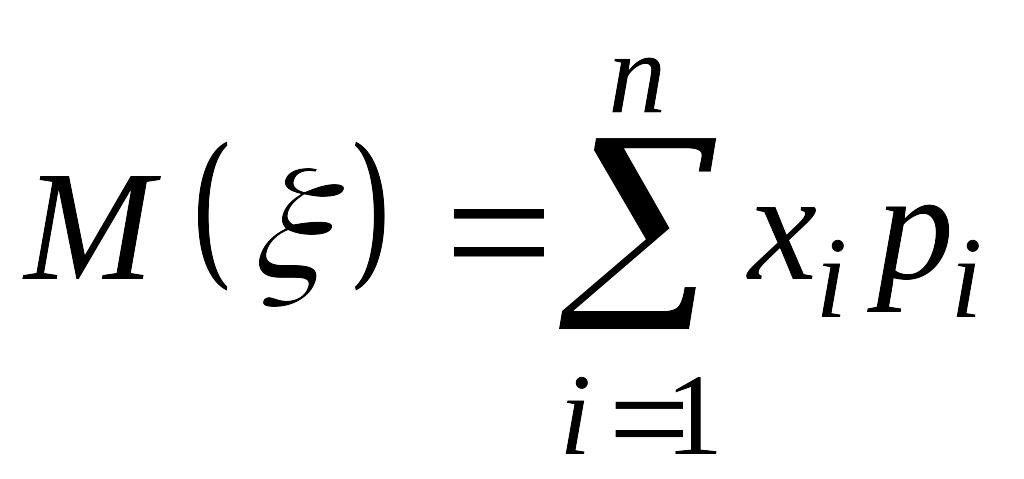 . (14.2)
. (14.2)
О: Математическим ожиданием непрерывной СВ с плотностью распределения называется
 (14.3)
(14.3)
Математическое ожидание имеет следующие свойства:
10.
Математическое ожидание постоянной
равно ей самой:![]() ,
,
![]() .
.
20.
![]() ,
,
![]() .
.
30.
![]() .
.
Если
задана дискретная СВ
![]() с законом распределения
,
то математическое ожидание определяется
как
в случае абсолютной сходимости ряда
справа. В противном случае СВ не имеет
математического ожидания.
с законом распределения
,
то математическое ожидание определяется
как
в случае абсолютной сходимости ряда
справа. В противном случае СВ не имеет
математического ожидания.
Для характеристики степени разбросанности значений СВ около её среднего значения вводится дисперсия.
О: Дисперсией СВ называется
![]() . (14.4)
. (14.4)
О: Средним квадратичным отклонением СВ называется
![]() . (14.5)
. (14.5)
Используя
(14.2) и (14.4) получаем для дискретной СВ
формулу
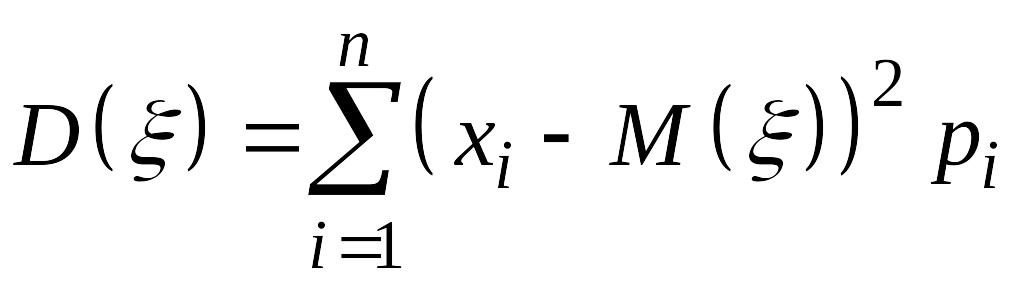 .
.
Для
непрерывной СВ
с плотностью вероятности
из (14.3) и (14.4) имеем
 .
.
Используя
свойства
![]() ,
запишем
,
запишем
![]() в другом виде:
в другом виде:
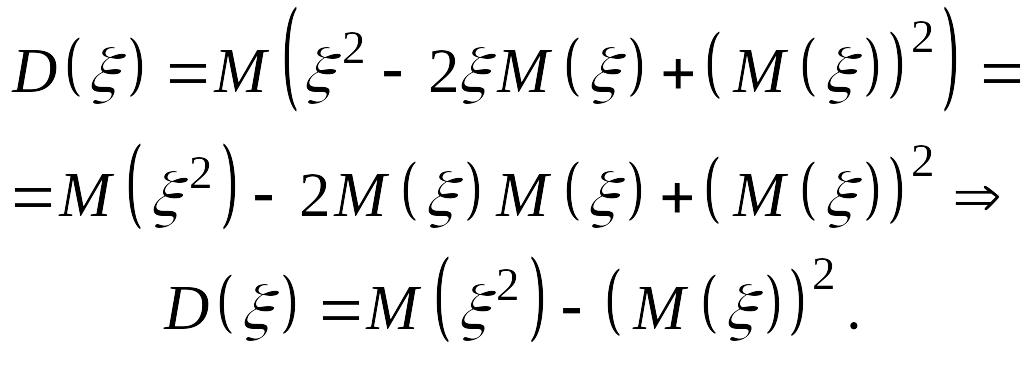 (14.6)
(14.6)
Дисперсия удовлетворяет следующим свойствам:
10.
![]() ,
.
,
.
20.
![]() ,
.
,
.
Свойства следуют из формулы (14.6) и свойств 10, 20 математического ожидания.
Примеры.
1) Бросается игральная кость.
![]() .
.![]() .
.
![]() .
.
2)
Вращающееся симметричное колесо
останавливается вследствие трения.
Угол
,
образованный некоторым фиксированным
подвижным радиусом колеса с неподвижным
радиусом после остановки колеса есть
случайная величина с плотностью
распределения:

Тогда,
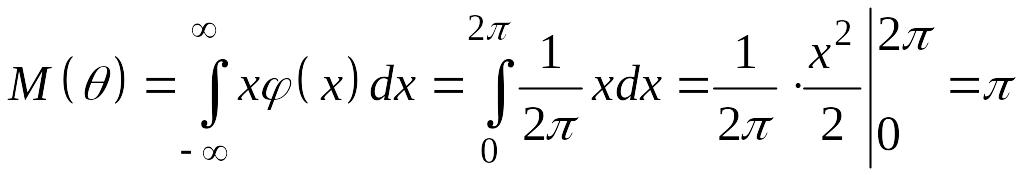 ,
,
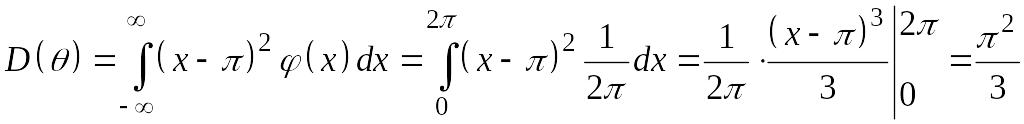 ,
,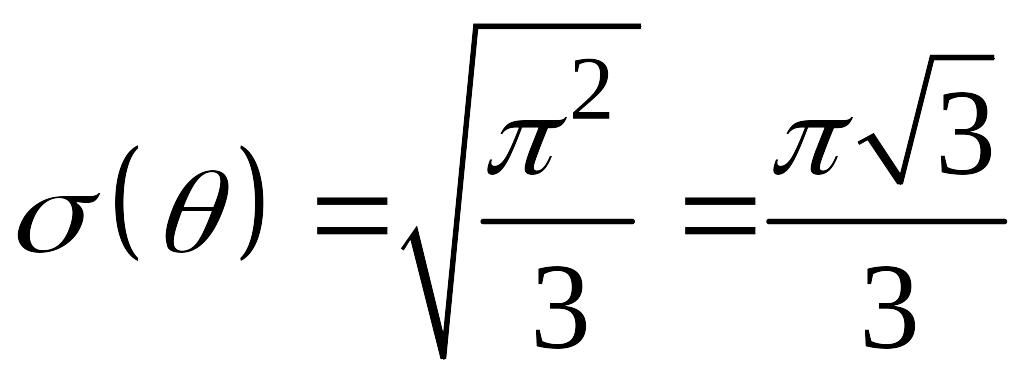 .
.
Примеры распределений дискретных и непрерывных СВ
1. Примеры распределения дискретной СВ
О:
Распределение дискретной СВ
называется равномерным, если оно задаётся
рядом
![]() .
.
Для
равномерного распределения по (14.2),
(14.6):
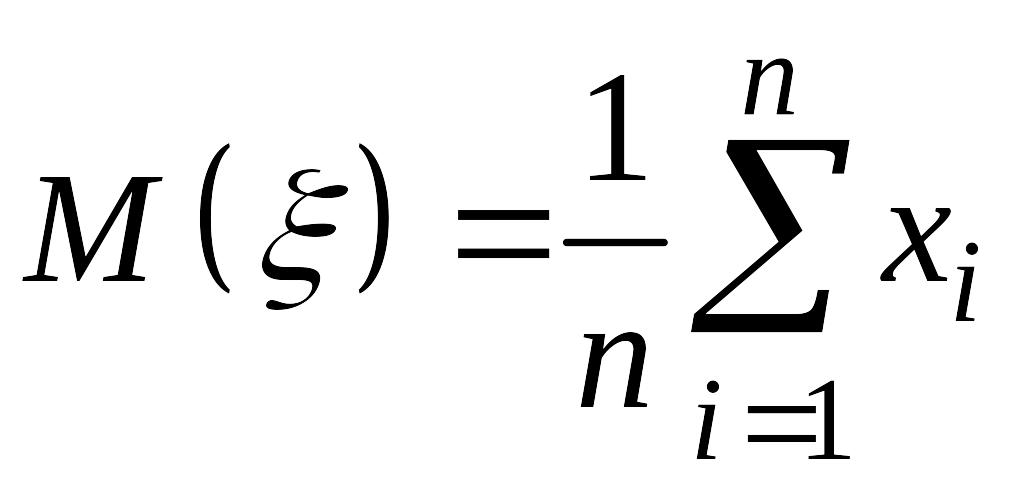 ,
,
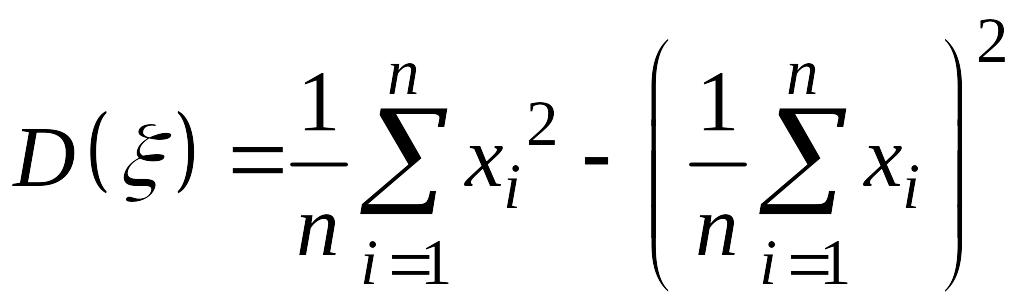 .
.
Пример такого распределения приведён в п. 14.1.
О: Распределение дискретной СВ называется биномиальным, если оно задаётся рядом
![]() ,
,
где
и
![]() имеют тот же смысл, что и для схемы
испытаний Бернулли.
имеют тот же смысл, что и для схемы
испытаний Бернулли.
Для
биномиального распределения СВ
математическое ожидание
![]() .
.
Дисперсия
для биномиального распределения
вычисляется по формуле
![]() .
.
Пример. Бросается игральная кость 10 раз. Событие - появление некоторой цифры, например 1, при каждом бросании, СВ - число возможных наступлений при десяти бросаниях кости. Тогда:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
О: Распределение дискретной СВ называется распределением Пуассона, если оно задано рядом
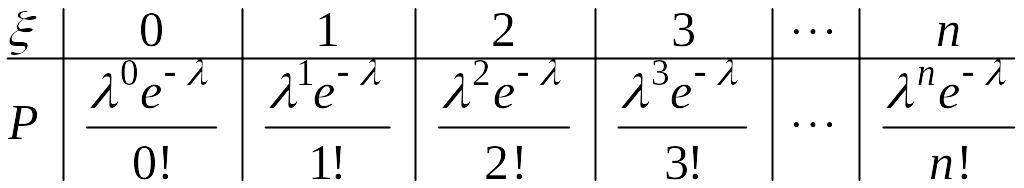 ,
,
и
удовлетворяют тем же условиям, что и в
формуле Пуассона.
,
,
и
удовлетворяют тем же условиям, что и в
формуле Пуассона.
Для
распределения Пуассона
![]() .
.
2. Примеры распределений непрерывной СВ
О:
Непрерывная СВ
,
все возможные значения которой заполняют
отрезок
,
называется равномерно распределённой,
если её плотность вероятности
![]() на
,
.
на
,
.
Так
как
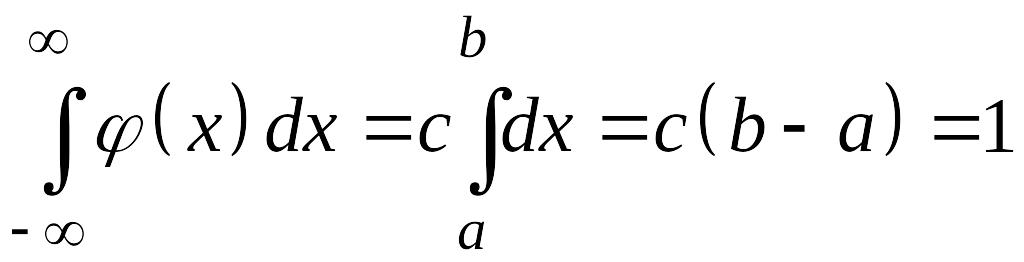 ,
то
,
то
![]() ,
т.е плотность равномерного распределения
,
т.е плотность равномерного распределения
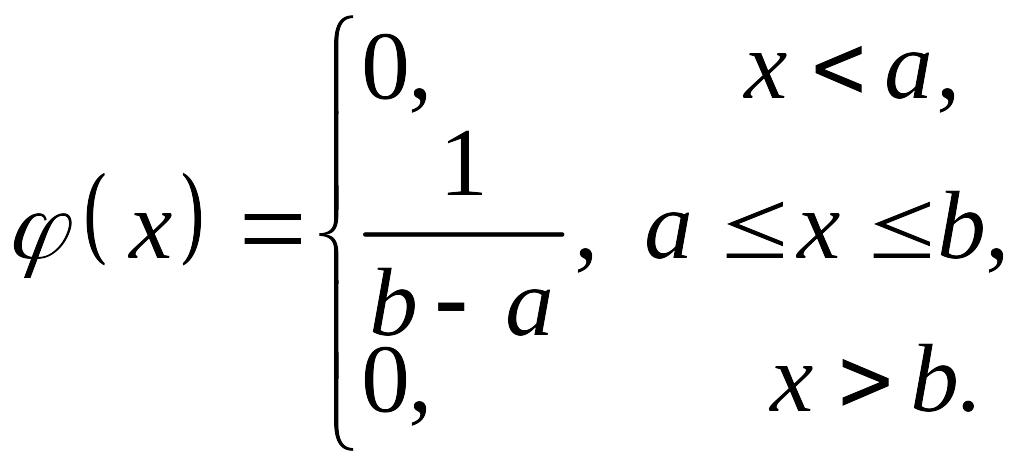
График плотности распределения изображён на рис. 14.4.
|
Рис. 14.4. |
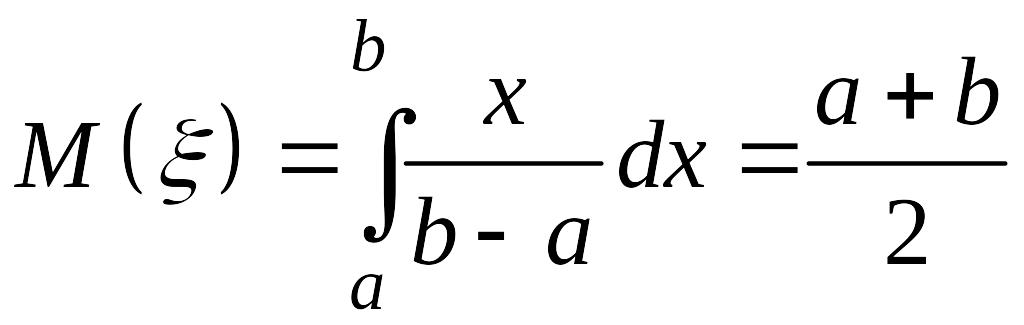 .
.
Дисперсию
получим по (14.6), используя
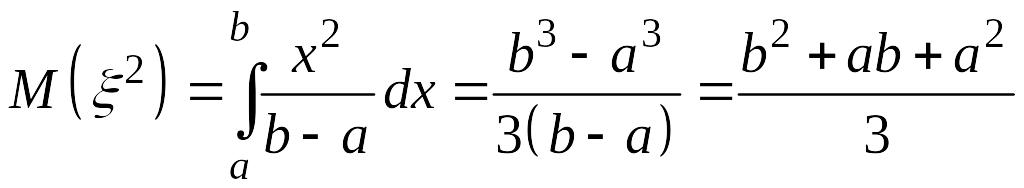 .
.
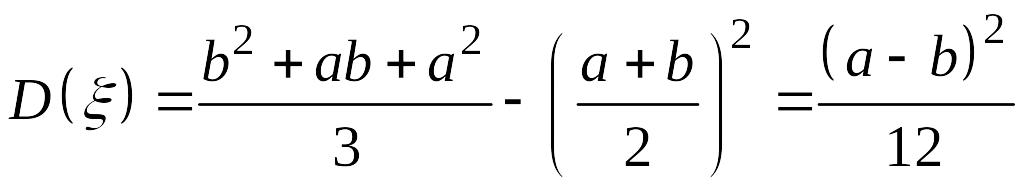 .
.
Вероятность
попадания СВ не отрезок
![]() находится по формуле (14.1):
находится по формуле (14.1):
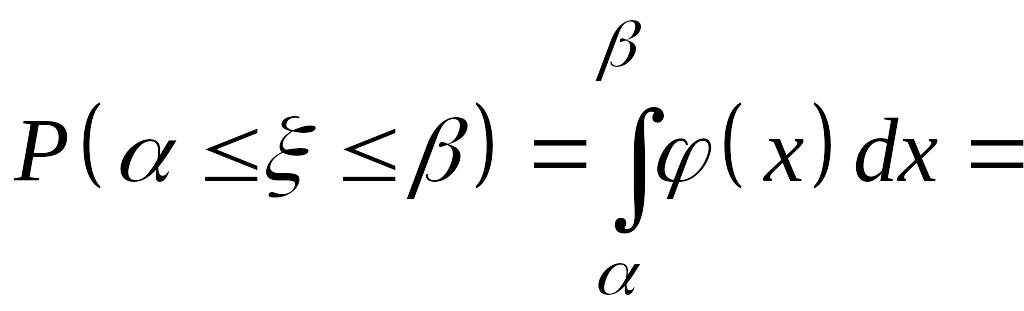
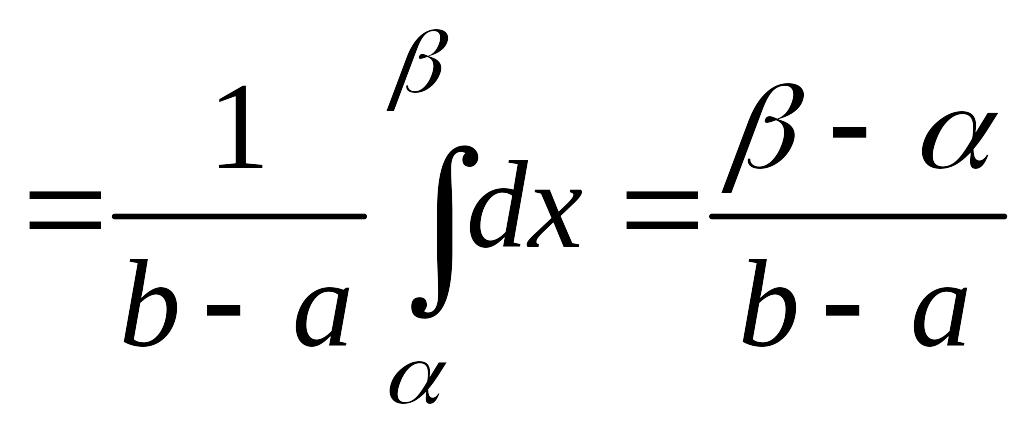 .
.
Пример.
Непрерывная СВ
имеет равномерный закон распределения
на
![]() .
Определить: 1. Вероятность попадания
в
.
Определить: 1. Вероятность попадания
в
![]() ;
2.
,
.
;
2.
,
.
Решение.
По условию плотность распределения
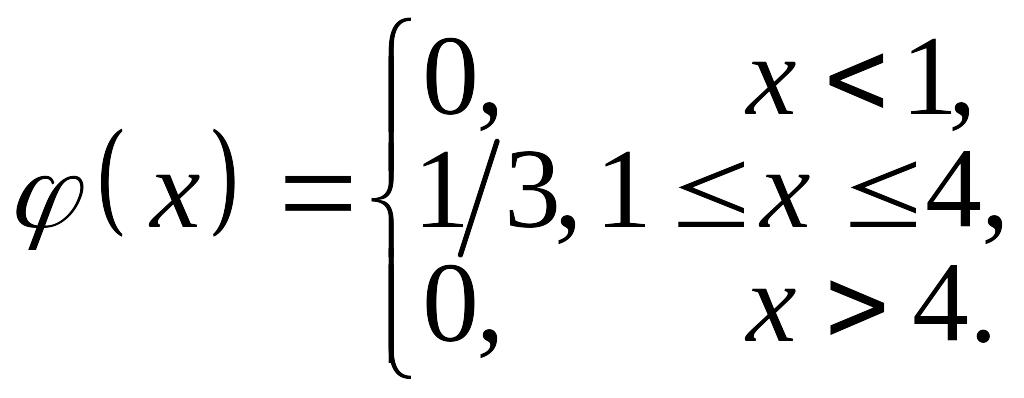 Отсюда 1)
Отсюда 1)
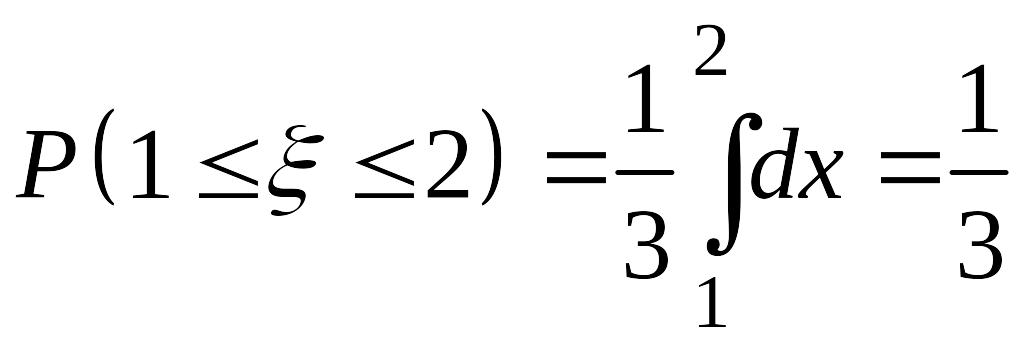 ;
2).
;
2).
![]() ;
;
 .
.
О:
Непрерывная СВ
называется нормально распределённой,
если её плотность распределения
 ,
,
![]() ,
,
,
,
![]() - некоторые постоянные.
- некоторые постоянные.
Функция
нормального распределения
 ,
,
где
смысл параметров
и
:
![]() ,
,
![]() и следовательно,
и следовательно,
![]() ‑ среднеквадратичное отклонение.
‑ среднеквадратичное отклонение.
|
Рис. 14.5. |
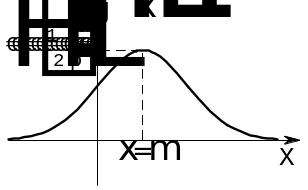 рафик
плотности распределения
(рис. 14.5) име-ет максимум в точке
рафик
плотности распределения
(рис. 14.5) име-ет максимум в точке
Пусть
необходимо найти вероятность того, что
СВ
попадёт в промежуток
![]() .
По (14.1)
.
По (14.1)

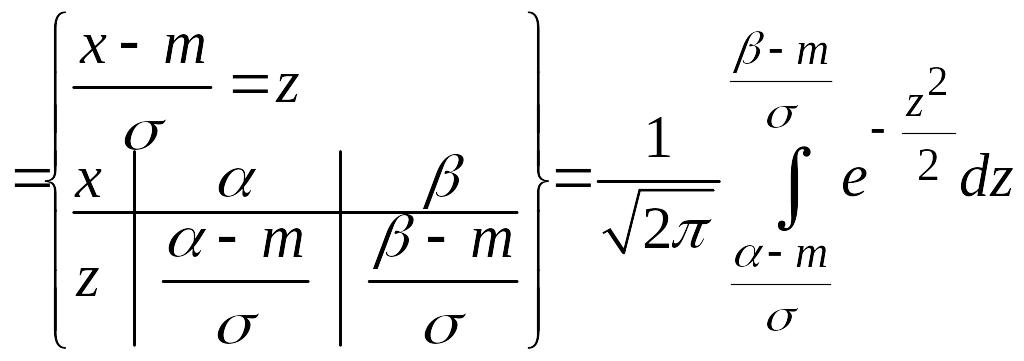 .
Нечётная функция
.
Нечётная функция
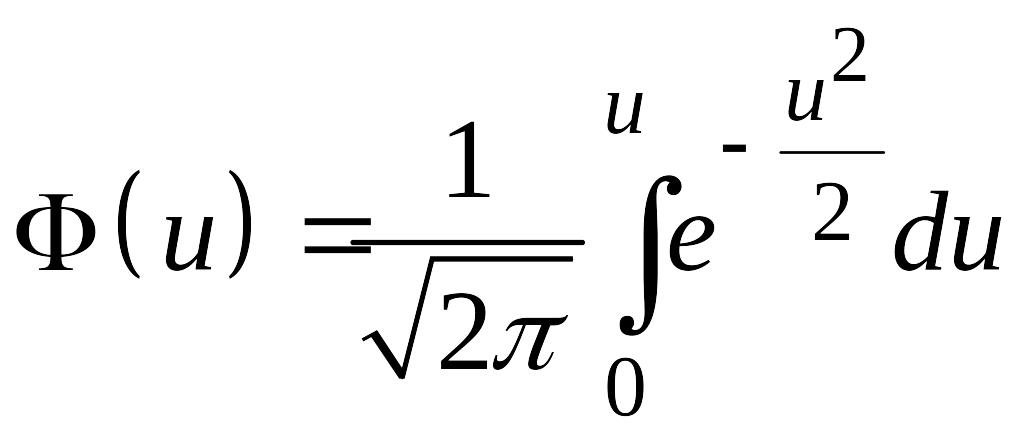 называется функцией Лапласа. Имеются
таблицы значений этой функции. Тогда:
называется функцией Лапласа. Имеются
таблицы значений этой функции. Тогда:
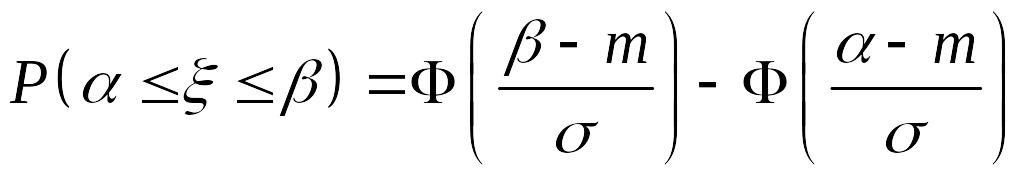 . (14.7)
. (14.7)
Пример.
СВ
имеет нормальное распределение с
параметрами
![]() ,
,
![]() .
Определить
.
Определить
![]() .
.
Решение.
По таблице значений функции Лапласа
находим
 ,
,
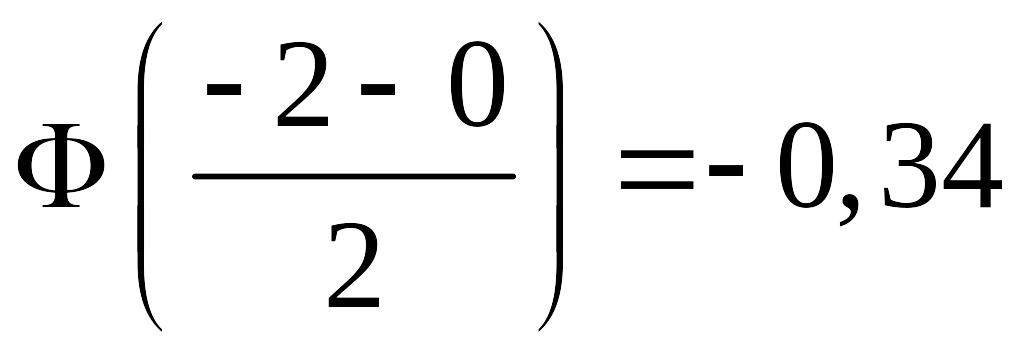 ,
т.е. по (14.6)
,
т.е. по (14.6)
![]() .
.

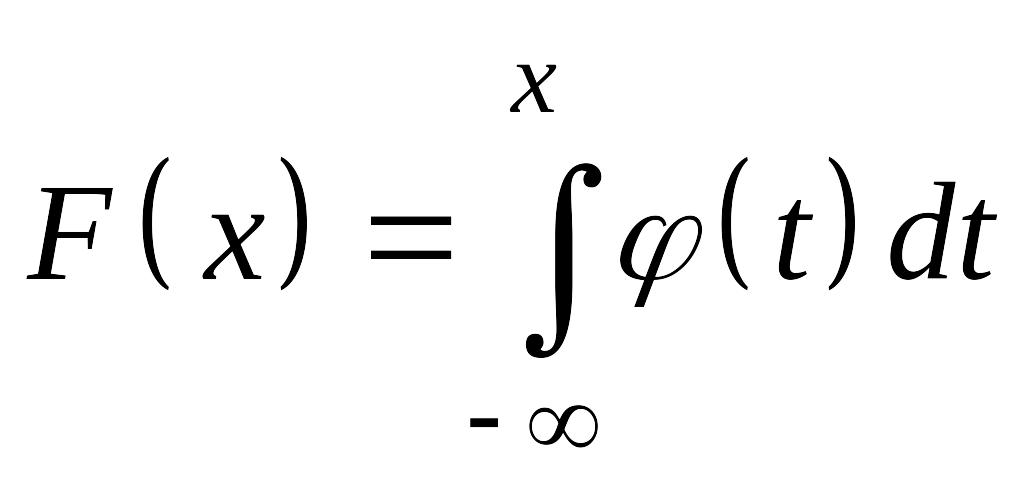 ,
,
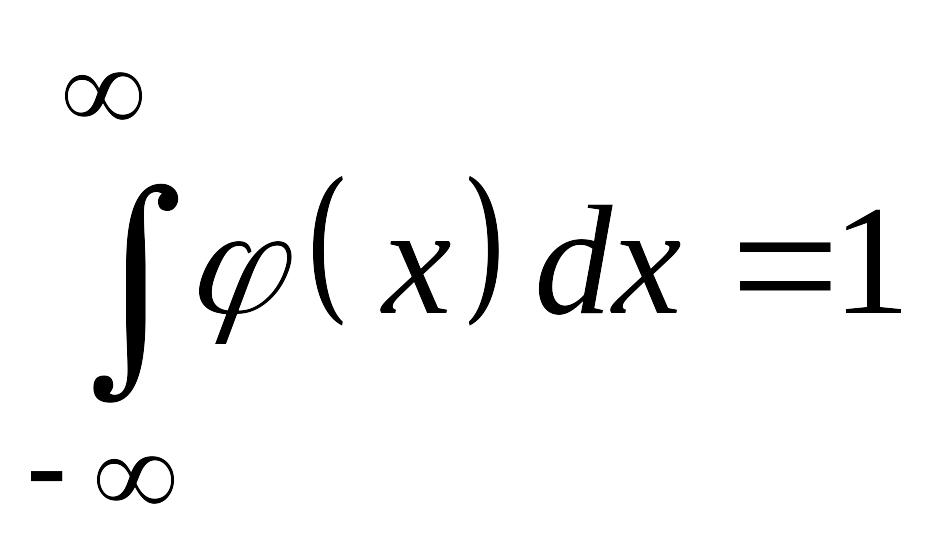 ,
,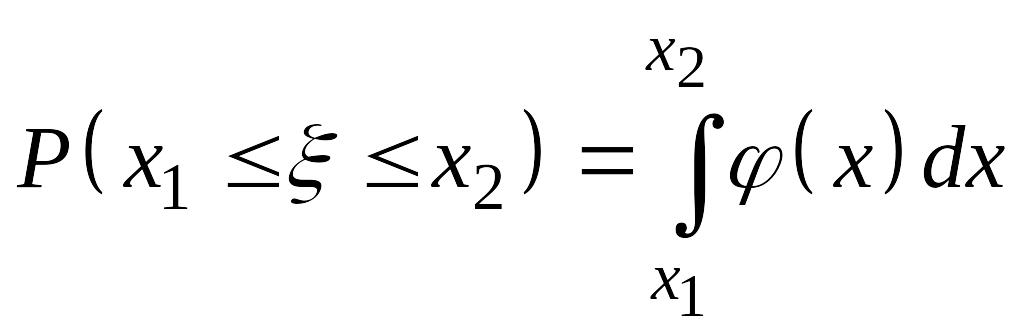
 .
. ,
,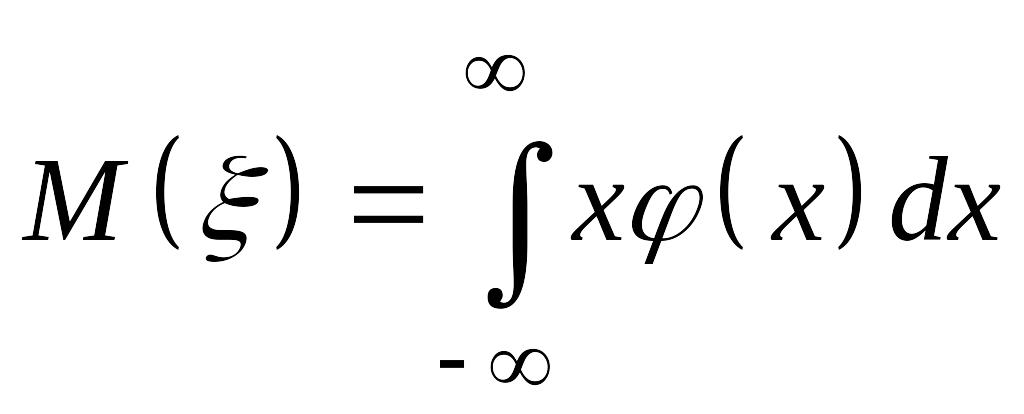 .
Дисперсия СВ
.
Дисперсия СВ