
- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
2. Геометрическое определение вероятности
Геометрическое определение вводится для пространства с бесконечным числом элементарных событий, каждое из которых интерпретируется как выбор наугад точки из некоторого множества евклидового пространства . Множество предполагается имеющим геометрическую форму и конечную меру .
О:
Вероятностью события
,
состоящего в попадании выбранной наугад
точки из измеримого множества
в измеримое множество
![]() ,
называется
,
называется
![]() .
.
Пример.
Два человека договариваются о встрече
на заданном промежутке времени
![]() .
Человек, пришедший первым, ожидает в
течение времени
.
Человек, пришедший первым, ожидает в
течение времени
![]() .
Какова вероятность встречи?
.
Какова вероятность встречи?
Множество
элементарных событий – квадрат
![]() ,
,
![]() ,
где
-
время прихода 1-го,
-
2-го. Событие
состоит
из элементарных событий,
,
где
-
время прихода 1-го,
-
2-го. Событие
состоит
из элементарных событий,
|
Рис. 13.2. |
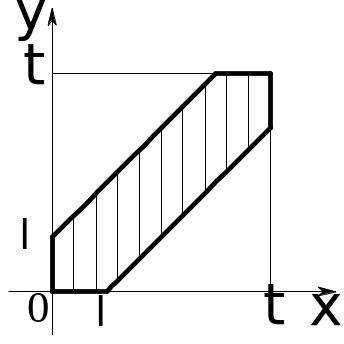 аходящихся
в полосе между прямыми
аходящихся
в полосе между прямыми
 .
.
3. Статистическое (частотное) определение вероятности
Пусть некоторый эксперимент повторяется раз, событие при этом наступило раз.
О:
Относительной частотой появления
события
,
наступившего
раз при проведении эксперимента
раз, называется
![]() .
.
Замечено,
что при больших
частота
![]() лишь слегка колеблется – это закон
устойчивости частот.
лишь слегка колеблется – это закон
устойчивости частот.
О:
Статистической
вероятностью события
называется
![]()
![]() ,
если число испытаний
достаточно большое.
,
если число испытаний
достаточно большое.
Например,
при бросании монеты 24000 раз герб выпал
12012 раз (опыт К. Пирсона). Число
![]() близко к
близко к
![]() .
При решении задачи о вероятности
выпадения герба при бросании монеты
формула (13.2) даёт
.
При решении задачи о вероятности
выпадения герба при бросании монеты
формула (13.2) даёт
![]() .
.
Сложение и умножение вероятностей
Т: Если и - несовместные события
![]() , (13.3)
, (13.3)
в противном случае
![]() . (13.4)
. (13.4)
Формула (13.4) справедлива и для вероятности суммы несовместных событий.
Следствие.
Вероятность противоположного событию
события
![]() равна
равна
![]() .
Из (13.3)
.
Из (13.3)
![]() .
.
Примеры.
1. В урне 2 зелёных, 4 жёлтых, 7 красных, 10 белых шаров. Вынимают один шар. Найти вероятность того, что он не белый.
Решение.
Пространство
содержит 23 элементарных события.
Случайное событие, состоящее в выборе
цветного шара
![]() .
Здесь
- событие, состоящее в выборе зелёного
шара,
- жёлтого,
.
Здесь
- событие, состоящее в выборе зелёного
шара,
- жёлтого,
![]() - красного. Так как
- красного. Так как
![]() ,
,
![]() ,
,
![]() ,
по формуле (13.3) имеем
,
по формуле (13.3) имеем
![]() .
.
2.
Вероятность того, что день пасмурный
![]() .
Найти вероятность того, что день ясный.
.
Найти вероятность того, что день ясный.
Решение.
Событие
,
состоящее в том, что день ясный,
противоположное событию
(день пасмурный), т.е.
![]() .
.
О: Вероятность события в предположении, что произошло событие , называется условной вероятностью и обозначается . События и называются независимыми, если предположение о том, что произошло одно из них, не влияет на вероятность другого, т.е.
![]() ,
. (13.5)
,
. (13.5)
Т:
Вероятность
![]() совместного наступления событий
и
вычисляется по формуле
совместного наступления событий
и
вычисляется по формуле
![]() (13.6)
(13.6)
Если события и независимы, то
![]() . (13.7)
. (13.7)
Эта формула справедлива и для вероятности произведения независимых событий.
Примеры.
1). Из урны, содержащей 3 белых и 7 чёрных шаров, вынимают два. Какова вероятность того, что оба шара белые?
Решение.
Событие
- вынут белый шар,
![]() .
Событие
- вынут второй белый шар при условии,
что произошло
,
.
Событие
- вынут второй белый шар при условии,
что произошло
,
![]() ,
тогда вероятность того, что оба шара
белые
,
тогда вероятность того, что оба шара
белые
![]() .
.
2.
Рабочий обслуживает три станка, работающих
независимо друг от друга. Вероятность
того, что в течение часа станок не
потребует внимания рабочего для первого
станка
![]() ,
для второго
,
для второго
![]() ,
для третьего
,
для третьего
![]() .
Найти вероятность того, что в течение
часа ни один станок не потребует внимания
рабочего.
.
Найти вероятность того, что в течение
часа ни один станок не потребует внимания
рабочего.
Решение.
По формуле (10.7) имеем
![]() .
.
Т:
пусть случайные события
![]() ,
образуют полную группу событий. Тогда
для любого случайного события
справедлива формула
,
образуют полную группу событий. Тогда
для любого случайного события
справедлива формула
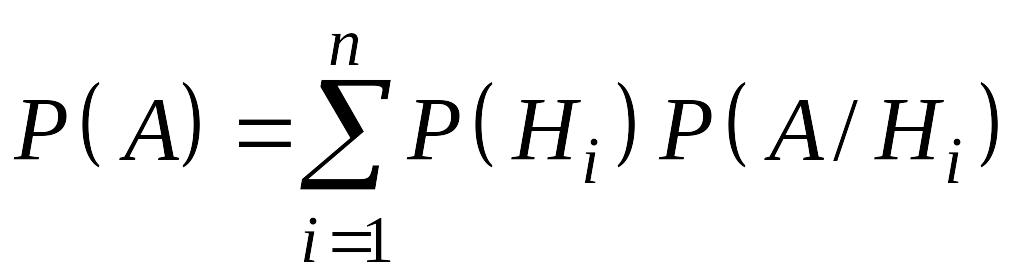 . (13.8)
. (13.8)
Эту формулу называют формулой полной вероятности.
Пример. Имеется два ящика с шарами. В первом ящике два белых и один чёрный шар, во втором ящике один белый и четыре чёрных шара. Наугад выбираем ящик и вынимаем шар. Какова вероятность того, что он белый?
Решение.
Пространство
![]() ,
где
,
где
![]() - выбор первого ящика,
- выбор первого ящика,
![]() - второго, событие
- выбор шара, тогда
- второго, событие
- выбор шара, тогда
![]() ,
,
![]() ,
,
![]() и по формуле (13.8)
и по формуле (13.8)
![]() .
.
Из
формулы
![]() и (13.8) получается так называемая формула
Байеса
и (13.8) получается так называемая формула
Байеса
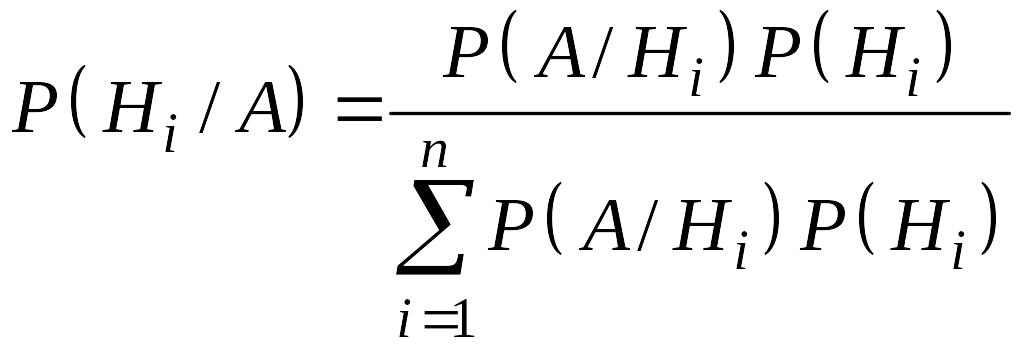 ,
. (13.9)
,
. (13.9)
Формула
трактуется следующим образом: имеется
полная группа гипотез
,
…,
![]() ,
вероятности которых известны до опыта.
Проводится опыт, в результате которого
может наступить или не наступить событие
.
Если событие
наступило, то (13.9) определяет вероятности
гипотез после опыта.
,
вероятности которых известны до опыта.
Проводится опыт, в результате которого
может наступить или не наступить событие
.
Если событие
наступило, то (13.9) определяет вероятности
гипотез после опыта.
Схема испытаний Бернулли
Пусть
один и тот же опыт повторяется
раз, испытания независимы, в результате
каждого испытания может наступить или
нет событие
.
Пусть
- вероятность наступления
,
тогда
![]() .
Такая схема испытаний называется схемой
Бернулли. Найдём вероятность
.
Такая схема испытаний называется схемой
Бернулли. Найдём вероятность
![]() того, что событие
произойдёт при
испытаниях
раз.
того, что событие
произойдёт при
испытаниях
раз.
Пространство
элементарных событий состоит из
произведений
событий
или
:
![]() ,
,
![]() ,
.
Событие
,
состоящее в том, что событие
произойдёт при
испытаниях
раз включает те
,
.
Событие
,
состоящее в том, что событие
произойдёт при
испытаниях
раз включает те
![]() ,
в которых
содержится
раз, их
,
в которых
содержится
раз, их
![]() .
По формуле (13.7):
.
По формуле (13.7):
![]() ,
поэтому по (12.3)
,
поэтому по (12.3)
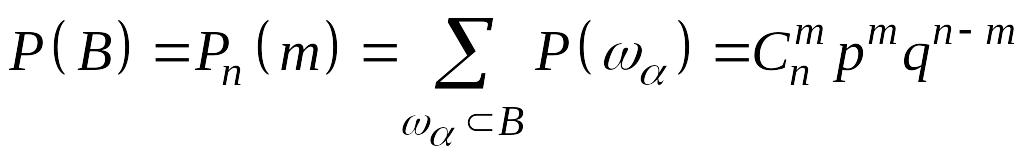 .
Формула
.
Формула
(13.10)
называется формулой Бернулли.
Пример. Найти вероятность того, что четырехзначный номер первого встречного автомобиля содержит две цифры 5.
Решение.
Так как
,
(число цифр в номере),
![]() ,
событие
- данная цифра номера 5,
- не 5,
,
событие
- данная цифра номера 5,
- не 5,
![]() ,
,
![]() ,
то
,
то
![]()
![]() .
.
При больших значениях , подсчёт проводят по приближённой формуле (локальная теорема Лапласа)
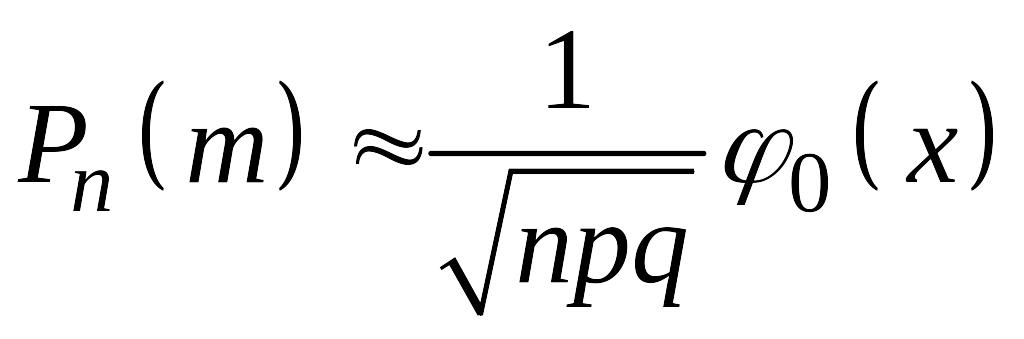 ,
,
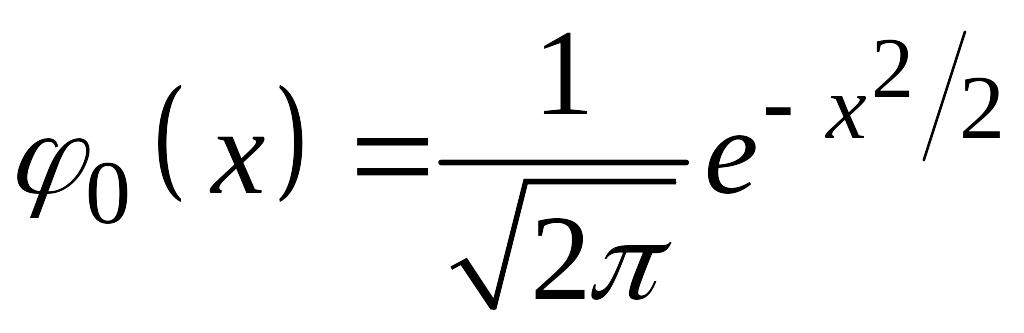 ,
,
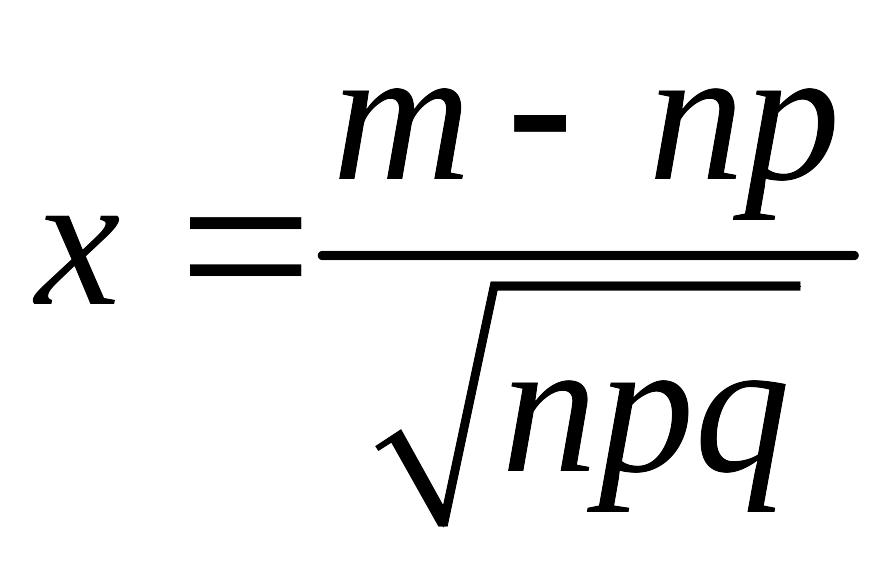 .
.
Если
велико, а
![]() ,
,
![]() ,
то применяют приближённую формулу
Пуассона:
,
то применяют приближённую формулу
Пуассона:
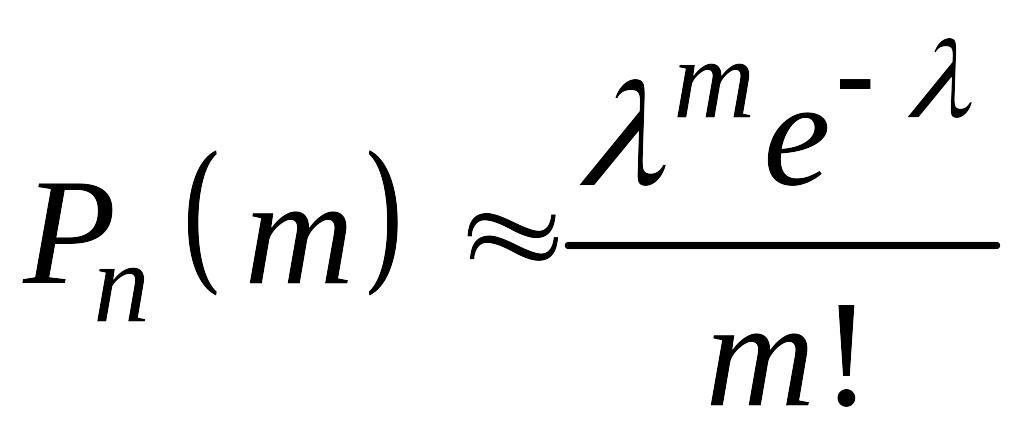 ,
,
![]() . (13.11)
. (13.11)
Последнюю формулу называют законом редких событий.
