- •Содержание
- •Введение
- •Объем дисциплины и виды учебной работы
- •Тематический план дисциплины
- •Программа курса
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •Тема 2. Элементы математического анализа.
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Планы аудиторных занятий
- •Методические рекомендации по изучению дисциплины и по организации самостоятельной работы студентов
- •Тема 1. Элементы линейной алгебры и аналитической геометрии.
- •1.1. Матрицы и определители
- •1.2.Действия над матрицами.
- •1.3.Системы линейных уравнений.
- •Элементы аналитической геометрии
- •Тема2 Элементы математического анализа
- •2.1. Функции одной переменной. Элементарные функции (фоп)
- •2.2. Предел и непрерывность функции одной переменной
- •2.3. Дифференцируемые функции одной переменной
- •2.4. Первообразная функция. Неопределенный интеграл и его свойства
- •Интегрирование функций. Таблица основных формул интегрирования
- •2.5. Методы интегрирования: непосредственное интегрирование, интегрирование по частям, замена переменной Непосредственное интегрирование
- •Определенный интеграл
- •Методы интегрирования
- •Тема 3. Основные понятия теории вероятностей и математической статистики.
- •Основные понятия теории вероятностей
- •Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
- •2. Геометрическое определение вероятности
- •3.2. Случайные величины
- •3.3.Элементы математической статистики
- •Примеры контрольных заданий.
- •Литература
- •Вопросы для подготовки к экзамену
Тема 3. Основные понятия теории вероятностей и математической статистики.
Для
вероятностных задач необходимо уметь
находить вероятность определенного
события
![]() .
При условии, что используется классическая
вероятностная схема с равновероятными
элементарными событиями, подсчет такой
вероятности сводится к вычислению
отношения
.
При условии, что используется классическая
вероятностная схема с равновероятными
элементарными событиями, подсчет такой
вероятности сводится к вычислению
отношения
![]() ,
где
,
где
![]() -
число всех элементарных событий, а
-
число всех элементарных событий, а
![]() - число элементарных событий, входящих,
в событие
.
Обычно для вычисления значений
и
используются методы комбинаторики.
- число элементарных событий, входящих,
в событие
.
Обычно для вычисления значений
и
используются методы комбинаторики.
Основные понятия теории вероятностей
Опорный конспект
1.
Понятие пространства элементарных
событий
О:
О:
Сс
|
3.Различные определения вероятности.
Аксиоматическое
и классическое определения
О:
Вероятность
1)
2)
наступления
О:
Вероятность
В классическом определении:
Геометрическое определение.
О: 3. Статистическое определение.
О:
|
2. Действия над случайными событиями.
Сумма
Произведение
Разность
,
О:
|
|
4. Сложение и умножение вероятностей
Т:
О:
,
-
независимы
Т:
Т:
|
|
5. Схема испытаний Бернулли Вероятность появления случайного события в независимых испытаниях раз:
|
Понятия пространства элементарных событий и случайного события. Основные формулы комбинаторики
Теория вероятностей изучает модели экспериментов, исходы которых неоднозначно определяются условиями опыта (случайного эксперимента).
О:
Элементарными событиями
называются всевозможные исходы опыта.
Пространством (множеством) элементарных
событий
называется совокупность всех элементарных
событий данного опыта:
![]() .
.
Будем считать, что - конечное или счётное множество.
Рассмотрим примеры.
1).
Бросается игральная кость. Количество
возможных исходов опыта
![]() ,
,
![]() ,
-
выпадение
.
,
-
выпадение
.
2).
Подбрасывается монета. Количество
возможных исходов
![]() ,
,
![]() ,
,
![]() -
выпадение герба,
-
выпадение герба,
![]() -
выпадение решки.
-
выпадение решки.
3).
Подбрасываются две монеты. Количество
возможных исходов
![]() ,
,
![]() .
.
При определении числа элементарных событий, входящих в конечное пространство , используются такие понятия комбинаторного анализа, как перестановки, сочетания, размещения.
О:
Соединениями называются различные
комбинации из элементов множества
![]() ,
подчинённые определённым условиям.
Перестановками из
элементов называются соединения,
содержащие
-
элементов и отличающиеся их порядком.
Размещениями из
элементов по
(
,
подчинённые определённым условиям.
Перестановками из
элементов называются соединения,
содержащие
-
элементов и отличающиеся их порядком.
Размещениями из
элементов по
(![]() )
называются соединения из
элементов, составленные из данных
элементов, отличающихся друг от друга
либо самими элементами, либо их порядком.
Сочетаниями из
элементов по
(
)
называются соединения из
элементов, составленные из данных
элементов, которые отличаются друг от
друга хотя бы одним элементом.
)
называются соединения из
элементов, составленные из данных
элементов, отличающихся друг от друга
либо самими элементами, либо их порядком.
Сочетаниями из
элементов по
(
)
называются соединения из
элементов, составленные из данных
элементов, которые отличаются друг от
друга хотя бы одним элементом.
Для подсчёта числа соединений существуют следующие формулы:
число перестановок из элементов: ;
число
размещений из
элементов по
:
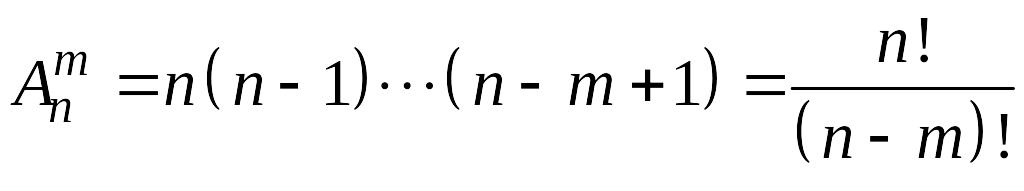 ;
;
число
сочетаний из
элементов по
:
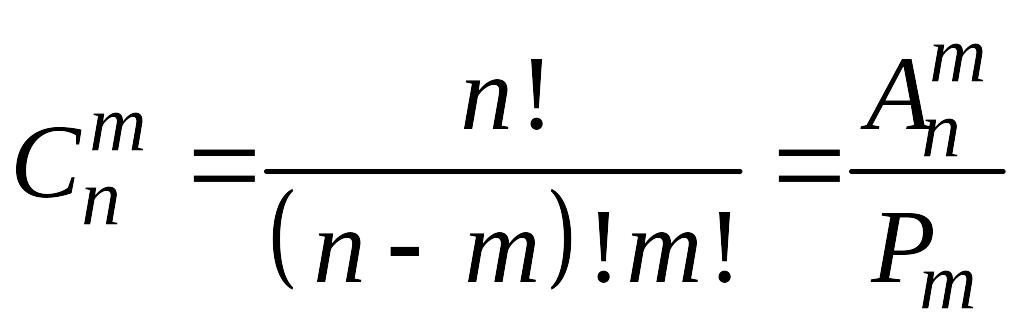 .
.
Пример.
![]() .
.
1).
Перестановки:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ;
;
![]() .
.
2).
Размещения из 3-х элементов по 2:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
3).
Сочетания из 3-х элементов по 2:
,
,
;
![]() .
.
О: Случайным событием называется подмножество множества элементарных событий: . называется достоверным событием, (пустое множество) – невозможным.
В результате эксперимента случайное событие может произойти или не произойти.
Примеры.
1).
Бросается игральная кость. Событие
- появление цифры
![]()
![]() ,
- появление
,
т.е. в
входят 3 элементарных события.
,
- появление
,
т.е. в
входят 3 элементарных события.
2).
Бросаются две игральные кости. Пространство
элементарных событий
![]() число элементарных событий 36. Пусть
- появление таких цифр (
число элементарных событий 36. Пусть
- появление таких цифр (![]() ),
что их сумма
),
что их сумма
![]()
![]() .
.
3).
Из карточек сложно слово из 6-ти букв
«победа». Выбираем наугад две буквы,
- обе выбранные буквы являются согласными.
Пространство элементарных событий
состоит из
![]() элементарных событий. Случайное событие
состоит из
элементарных событий. Случайное событие
состоит из
![]() элементарных событий.
элементарных событий.
. Действия над событиями
Действия над случайными событиями и отношения между ними определяются по аналогии с действиями и отношениями в теории множеств.
Обозначим
![]() ,
если
- элементарный исход события
;
,
если
- элементарный исход события
;
![]() ,
если событие
влечёт за собой
;
,
если событие
влечёт за собой
;
![]() .
.
Равенство
(эквивалентность) событий:
![]() ,
если
и
,
если
и
![]() .
.
О:
Суммой
![]()
![]() событий
и
называется их теоретико-множественное
объединение, т.е. событие, состоящее из
элементарных событий
:
событий
и
называется их теоретико-множественное
объединение, т.е. событие, состоящее из
элементарных событий
:
![]() или
или
![]() .
.
О:
Произведением
![]()
![]() событий
и
называется их теоретико-множественное
пересечение, т.е. событие, состоящее из
элементарных событий
:
и
.
событий
и
называется их теоретико-множественное
пересечение, т.е. событие, состоящее из
элементарных событий
:
и
.
О:
Разностью
![]() событий
и
называется их теоретико-множественная
разность, т.е. событие, состоящее из
элементарных событий :
:
,
но
событий
и
называется их теоретико-множественная
разность, т.е. событие, состоящее из
элементарных событий :
:
,
но
![]() .
.
О:
Противоположным событием
![]() для события
называется теоретико-множественное
дополнение
до
,
т.е.
происходит тогда, когда
не происходит.
для события
называется теоретико-множественное
дополнение
до
,
т.е.
происходит тогда, когда
не происходит.
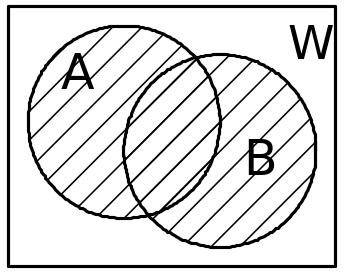
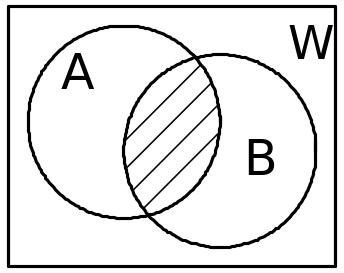
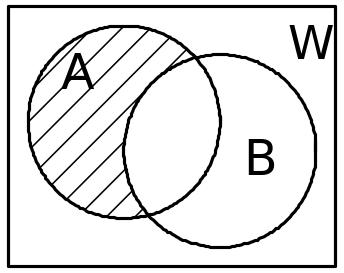
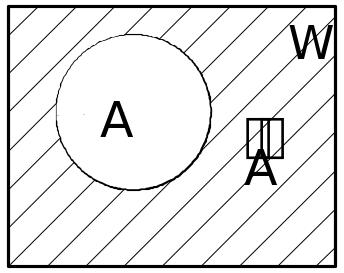
Если изобразить геометрически областью на плоскости, а элементарные события - элементами этой области, то действия над событиями можно изобразить схематически (рис. 13.1).
|
|
|
|
|
|
|
Рис. 13.1 |
||||||
Примеры.
1.
- выигрыш по 1 займу;
- выигрыш по 2 займу. Тогда
![]() - выигрыш хотя бы по одному из займов (в
частности, сразу по двум).
- выигрыш хотя бы по одному из займов (в
частности, сразу по двум).
2. - прохождение I тура на конкурсе, - прохождение II тура. Тогда - успешное прохождение I и II туров.
3. Бросается монета. - выпадение герба, - выпадение решки.
Множество
случайных событий
![]() и
образуют Булеву алгебру – алгебру
событий, связанных с заданным экспериментом.
и
образуют Булеву алгебру – алгебру
событий, связанных с заданным экспериментом.
О: События и называются несовместными, если наступление события исключает наступление события , т.е. . В этом случае используют .
Таким образом , - несовместные события.
О:
Множество (система) событий
![]() ,
,
![]() ,
…,
,
…,
![]() ,
…,
,
…,
![]() ,
,
![]() называется полной группой событий
называется полной группой событий
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
Пример.
На трёх станках производятся болты,
которые складываются вместе. Берут
наугад один болт. За
считаем множество всех болтов, а полная
группа
![]() ,
где
,
где
![]() - случайное событие, состоящее в том,
что болт сделан на
-м
станке.
- случайное событие, состоящее в том,
что болт сделан на
-м
станке.
Различные определения вероятности
1. Аксиоматическое и классическое определения
Пусть
с данным опытом связано конечное или
счётное пространство элементарных
событий
![]() .
.
О:
Вероятностью
![]() элементарного события
называется действительное число,
удовлетворяющее условиям
элементарного события
называется действительное число,
удовлетворяющее условиям
1)
![]() ;
2)
;
2)
и определяющее меру наступления .
Рассмотрим теперь случайное событие .
О:
Вероятностью
![]() случайного события
называется действительное число,
определяемое формулой
случайного события
называется действительное число,
определяемое формулой
![]() . (13.1)
. (13.1)
Из
определения следует, что
![]() ,
,
.
Таким образом,
.
,
,
.
Таким образом,
.
Пусть
,
причём все
являются равновозможными и
содержит
элементарных событий. Тогда все
одинаковы, т.е.
![]() и по (12.1)
и по (12.1)
![]() . (13.2)
. (13.2)
Формулу
(13.2), являющуюся частным случаем (13.1),
принимают за классическое определение
вероятности в случае
равновозможных попарно несовместных
исходов опыта. События
![]() называют в этом случае благоприятствующими
наступлению
.
называют в этом случае благоприятствующими
наступлению
.
Примеры.
1.
Бросаются две игральные кости. Найти
вероятность того, что сумма выпавших
цифр
![]() .
.
Пространство
содержит 36 равновозможных элементарных
событий (см. пример 2 п. 13.1), случайное
событие
- 6 событий, т.е.
![]() .
.
2. В урне 2 зелёных, 4 жёлтых, 7 красных, 10 белых шаров. Вынимают один шар. Какова вероятность того, что он зелёный?
Пространство
состоит из
![]() событий, случайное событие
из двух событий, т.е.
событий, случайное событие
из двух событий, т.е.
![]() .
.

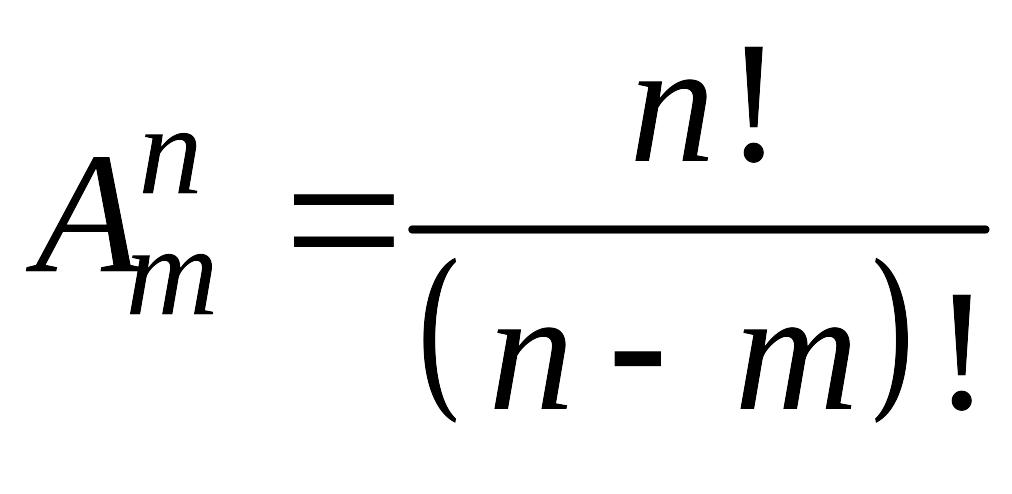 -
число размещений из
по
,
-
число размещений из
по
,
 - число сочетаний из
по
.
- число сочетаний из
по
.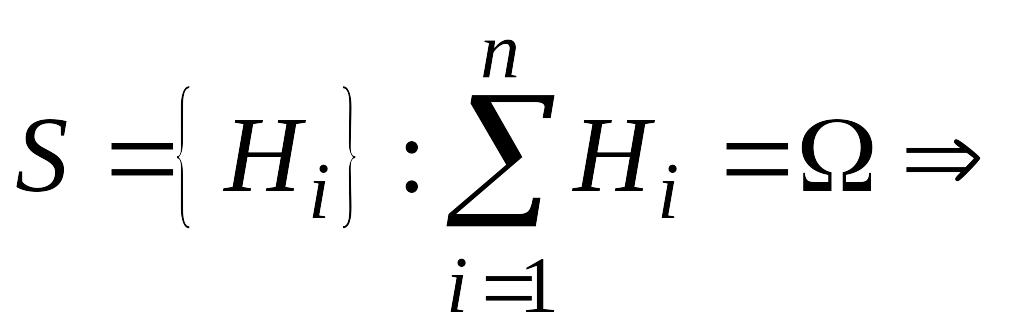
 ,
,