43. Гра 2х2 в змішаних стратегіях. Алгоритм розв’язування задачі.

Найпростішим випадком скінченої гри є парна гра, коли у кожного учасника є дві стратегії (табл. 8.4.1).

Таблиця 8.4.1.

Розглянемо випадок, коли гра не має сідловок точки. Отже, . Необхідно знайти змішані стратегії та ціну гри. Позначимо шукані значення ймовірностей застосування «чистих» стратегій гравця А через , а для гравця В – через .

Згідно з основною теоремою теорії ігор, якщо гравець А притримується своєї оптимальної стратегії, то виграш дорівнюватиме ціні гри. Отже, якщо гравець А притримуватиметься своєї оптимальної стратегії , то:

(8.4.1)

Оскільки , то . Підставивши цей вираз у систему рівнянь (8.4.1), отримаємо:

.

Розв’язавши дане рівняння відносно невідомого , маємо: , тоді

Провівши аналогічні міркування стосовно гравця В, маємо:

(8.4.2.)

Оскільки , то .

.

Розв’язавши це рівняння відносно невідомого , маємо: , тоді

Ціну гри знаходять, підставляючи значення (або ) в будь-яке з рівнянь (8.4.1) або (8.4.2): .

44. Зведення гри двох осіб до задачі лінійного програмування.

Найпростіший вид стратегічної гри — гра двох осіб з нульовою сумою (сума виграшів сторін дорівнює нулю). Тут мета одного гравця — максимізувати свій виграш, а другого — мінімізувати свій програш, причому рішення про вибір стратегії кожним гравцем приймається в умовах невизначеності, коли наперед не відомо, як вчинить супротивник. Якщо матрична гра не має сідлової точки, то знаходження її розв'язку, особливо за великої кількості стратегій, — доволі складна задача, яку можна ефективно розв'язати методами лінійного програмування.

Задача розглядається в такому формулюванні: знайти вектори ймовірностей і з метою визначення оптимального значення ціни гри та оптимальних стратегій.

Отже, нехай маємо скінченну матричну гру з платіжною матрицею

Оскільки оптимальні стратегії гравців А і В дозволяють отримати виграш

то використання оптимальної змішаної стратегії гравцем А має за безпечувати виграш не менший за ціну гри в разі вибору гравцем В будь-яких стратегій. Математично ця умова записується так:

(6.23)

Відповідно використання оптимальної змішаної стратегії грав цем В має за будь-яких стратегій гравця А забезпечувати програш В, що не перевищує ціни гри :

(6.24)

Ці два співвідношення застосовують для знаходження розв'язку гри.

Отже, потрібно знайти , щоб ;за умов

Зауважимо, що ціна гри невідома і має бути визначена під час розв'язування задачі.

Модель ігрової задачі може бути спрощена. З (6.23) маємо:

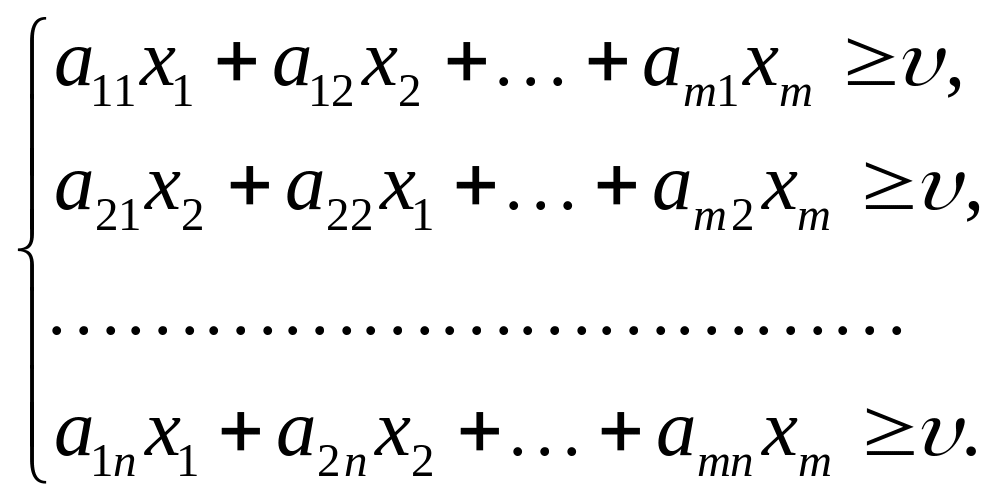
Поділивши всі обмеження на , дістанемо:

Нехай , тоді

Згідно з умовою , звідки .

Отже, цільова функція початкової задачі набирає такого вигляду:

.

У результаті лінійного програмування:

(6.25)

за умов

(6.26) (6.27)

Розв'язавши цю задачу симплексним методом, знайдемо значення , а також і , тобто визначимо змішану оптимальну стратегію для гравця А.

За аналогією запишемо задачу лінійного програмування для визначення оптимальної стратегії гравця В. Нехай

.

Тоді маємо таку лінійну модель:

за умов

Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв'язок однієї з них визначає оптимальний розв'язок спряженої.