Смысл формулы Больцмана

В условиях равновесия энтропия - функция состояния системы, которую можно измерить или вычислить теоретически. Но стоит изолированной системе отклониться от равновесия - возникает свойство энтропии - она только возрастает.

Представим формулу (1) в виде

P = e^S/K

и обратим внимание на то, что статистический вес состояния системы P экспоненциально растет с ростом S. Иными словами, менее упорядоченное состояние (больший хаос) имеет больший статистический вес^*, т. к. оно может быть реализовано большим числом способов. Следовательно, энтропия - мера неупорядоченности системы.

Из-за случайных перекладываний растет беспорядок на столе, в комнате. Порядок создается искусственно, беспорядок - самопроизвольно, т. к. ему отвечает большая вероятность, большая энтропия. Разумная деятельность человека направлена на преодоление разупорядоченности.

Обратим внимание на то, что первое начало термодинамики (закон сохранения энергии) - закон абсолютно строгий, это детерминированный закон. Второе начало термодинамики - закон возрастания энтропии - закон статистический (вероятностный).

Существует даже вероятность того, что молекулы, находящиеся в кубике размером 1 см³ могут все собраться в одной половине этого кубика. Вероятность для одной молекулы находиться в правой части кубика: q₁=1/2. При нормальных условиях в 1 см³ содержится число молекул 2,7*10¹⁹ (число Лошмидта), тогда вероятность того, что все молекулы соберутся в правую половину кубика равна   . Это исчезающе малая величина.

Работа Больцмана - прорыв в совершенно новую область: в физику вошла вероятность, статистические законы. Это значит, что хотя и редко, но энтропия может и убывать.

67.

Ван-дер-ваальсовы силы — силы межмолекулярного взаимодействия с энергией 0,8 — 8,16 кДж/моль. Этим термином первоначально обозначались все такие силы, в современной науке он обычно применяется к силам, возникающим при поляризации молекул и образовании диполей. Открыты Я. Д. ван дер Ваальсом в 1869 году.

К ван-дер-ваальсовым силам относятся взаимодействия между диполями (постоянными и индуцированными). Название связано с тем фактом, что эти силы являются причиной поправки на внутреннее давление в уравнении состояния реального газа Ван-дер-Ваальса. Эти взаимодействия в основном определяют силы, ответственные за формирование пространственной структуры биологических макромолекул.

Ван-дер-ваальсовы силы также возникают между частицей (макроскопической частицей или наночастицей) и молекулой и между двумя частицами.^[1][2][3]

Классификация ван-дер-ваальсовых сил

Ван-дер-ваальсовое взаимодействие состоит из трех типов слабых взаимодействий:

• Ориентационные силы, диполь-дипольное притяжение. Осуществляется между молекулами, являющимися постоянными диполями. Примером может служить HCl в жидком и твердом состоянии. Энергия такого взаимодействия обратно пропорциональна кубу расстояния между диполями.

• Дисперсионное притяжение (лондоновские силы). Взаимодействием между мгновенным и наведенным диполем. Энергия такого взаимодействия обратно пропорциональна шестой степени расстояния между диполями.

• Индукционное притяжение. Взаимодействие между постоянным диполем и наведенным (индуцированным). Энергия такого взаимодействия обратно пропорциональна шестой степени расстояния между диполями.

До сих пор многие авторы исходят из предположения, что ван-дер-ваальсовые силы определяют межслоевое взаимодействие в слоистых кристаллах, что противоречит экспериментальным данным: масштабу анизотропии температуры Дебая и, соответственно, масштабу анизотропии решёточного отражения. Исходя из данного ошибочного^[4] предположения построены многие двумерные модели, «описывающие» свойства, в частности графита и нитрида бора.

Величина энергии взаимодействия зависит от значений дипольных моментов и взаимного расположения диполей. Молекулярной ориентации такого рода противодействует тепловое движение, поэтому энергия ориентационного взаимодействия в значительной степени зависит от температуры:

 

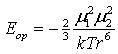
где М1 и М 2 – дипольные моменты взаимодействующих молекул; k – константа Больцмана (k = 1,38066·10²³ Дж/К); Т – температура; r – расстояние между молекулами. Индукционные, или деформационные, силы возникают при взаимном притяжении постоянных и наведенных диполей. Дипольная молекула может влиять на неполярные молекулы и вызывать некоторое смещение электронов и ядер окружающих молекул (поляризацию), при этом возникает наведенный диполь. Постоянный и наведенный диполи взаимно притягиваются. Энергия индукционного взаимодействия возрастает с увеличением дипольного момента и быстро уменьшается с увеличением расстояния между ними, а также не зависит от температуры (т.к. наведение диполей происходит при любом пространственном расположении молекул): 

 

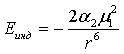
где а 2   – величина поляризуемости неполярной молекулы.

Дисперсионные силы обусловлены движением электронов в молекулах. Систему «электрон – ядро» можно рассматривать как диполь, отрицательный полюс которого (электрон) быстро перемещается. В молекулах, находящихся на небольшом расстоянии друг от друга, движение электронов становится в известной мере согласованным, и диполи часто оказываются обращенными друг к другу противоположно заряженными полюсами. Вследствие этого возникает притяжение молекул. Энергия дисперсионного взаимодействия тем больше, чем слабее связь электронов с ядрами; она не зависит от температуры:

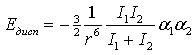
где а 1   и  а 2  – величины поляризуемости двух взаимодействующих молекул; I 1   и I 2 – ионизационные потенциалы молекул.

Силы Ван-дер-Ваальса являются близкодействующими силами и действуют на расстоянии 3-5 Å (0,3 – 0,5 нм). Энергия индукционных взаимодействий Е инд. мала и не превышает 5% от суммарного эффекта; вклад энергии дисперсионных взаимодействий Е дисп. является наиболее значительным (до 80–90% от суммарного эффекта), однако для молекул с большими дипольными моментами энергия ориентационных взаимодействий Еор   может приближаться к дисперсионной или даже превышать её.

         Особое место среди межмолекулярных сил занимают водородные связи. Они прочнее сил Ван-дер-Ваальса и существенно влияют на свойства полимеров. Водородная связь возникает между атомом водорода, связанного ковалентной связью, и другим атомом, имеющим большую электроотрицательность и хотя бы одну неподеленную пару электронов (фтор, кислород, азот, хлор, сера). Другими словами, это связь между двумя электроотрицательными атомами через водород. Водородные связи возможны, если в макромолекуле содержатся гидроксильные, карбоксильные, амидные и другие подобные группировки. Энергия водородной связи невелика (20–35 кДж/моль). Она меньше величины валентных сил, но больше сил Ван-дер-Ваальса.

         С возрастанием молекулярной массы вещества суммарные силы межмолекулярного взаимодействия могут превышать валентные силы. Так, энергия ковалентной связи между атомами углерода составляет              290 кДж, а в молекуле полиэтилена со степенью полимеризации 1000 суммарная энергия межмолекулярного взаимодействия достигает 840 кДж.

            В связи с полидисперсностью полимеров суммарные силы межмолекулярного взаимодействия вычисляют в расчете на мономерное звено. Вычисленная таким образом величина называется молярной энергией когезии.    

68.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, чтореальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия Uстановится функцией не только температуры, но и объёма.

Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

• p — давление,

• V — молярный объём,

• T — абсолютная температура,

• R — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

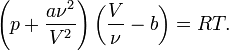
где

• V — объём,

69.

 Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V ² и раскрыв скобки, получаем

       PV ³ – (RT + bP) vV ² + av²V - abv³ = 0.

       Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке 7.4. Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Т_кр, которая разделяет немонотонные T < T_кр и монотонные T > Т_кр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Т_кр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермы Т₁ давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLB и AGE давление падает с увеличением объема (dP/dV)_Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD (жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL.

       При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.

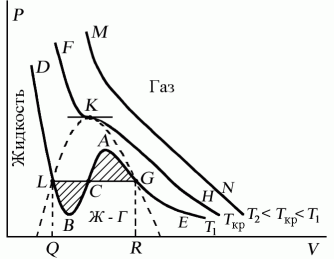  Рис. 7.4

       Наличие критической точки на изотерме Ван–дер–Ваальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии. К этому заключению пришел и Д.И. Менделеев в 1861 г. Он заметил, что при определенной температуре прекращалось поднятие жидкости в капиллярах, т.е. поверхностное натяжение обращалось в нуль. При той же температуре обращалась в нуль скрытая теплота парообразования. Такую температуру Менделеев назвал температурой абсолютного кипения. Выше этой температуры, согласно Менделееву, газ не может быть сконденсирован в жидкость никаким увеличением давления.

       Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна (рис. 7.5). Ее можно определить также как точку, в которую в пределе переходят горизонтальные участки изотерм при повышении температуры до критической. На этом основан способ определения критических параметров P_k, V_k, Т_k, принадлежащий Эндрюсу. Строится система изотерм при различных температурах. Предельная изотерма, у которой горизонтальный участок LG (рис. 7.4) переходит в точку, будет критической изотермой, а указанная точка – критической точкой 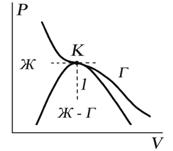(рис. 7.5).

  Рис. 7.5

70.

Фазовые переходы первого рода — фазовые переходы, при которых скачком изменяются первые производные термодинамических потенциалов по интенсивным параметрам системы (температуре или давлению). Переходы первого рода реализуются как при переходе системы из одного агрегатного состояния в другое, так и при в пределах одного агрегатного состояния (в отличие от фазовых переходов второго рода, которые происходят в пределах одного агрегатного состояния).

Примеры фазовых переходов первого рода

• при переходе системы из одного агрегатного состояния в другое: кристаллизация (переход жидкой фазы в твердую), плавление (переход твердой фазы в жидкую), конденсация (переход газообразной фазы в твердую или жидкую), взгонка (переход твердой фазы в газообразную), эвтектическое, перитектическое и монотектическое превращения.

• в пределах одного агрегатного состояния: эвтектоидное, перитектоидное и полиморфное превращения, распад пересыщенных твердых растворов, распад (расслоение) жидких растворов, упорядочение твердых растворов.

Иногда к фазовым переходам первого рода относят также мартенситные превращения (условно, так как в ходе мартенситного превращения реализуется переход в стабильное, но неравновесное состояние — метастабильное состояние).

   Фазовые переходы второго рода — фазовые переходы, при которых первые производные термодинамических потенциалов по давлению и температуре изменяются непрерывно, тогда как их вторые производные испытывают скачок. Отсюда следует, в частности, что энергия и объём вещества при фазовом переходе второго рода не изменяются, но изменяются его теплоёмкость, сжимаемость, различные восприимчивости и т. д.

Примеры фазовых переходов второго рода

• переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность),

• переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата),

• переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты),

• переход аморфных материалов в стеклообразное состояние.