43. Средняя квадратичная скорость.

Средняя квадратичная скорость поступательного движения молекул газа это корень из среднего арифметического значения квадратов скоростей молекул газа.

Средняя квадратичная скорость характеризует движение не одной частицы, а движение совокупности частиц. Молярная масса - масса 1 моль вещ-ва.

В одном моле любого вещества содержится одинаковое количество частиц равное постоянной Авогадро. NA

Средняя кинетическая энергия молекул.

<Wk> - средняя кинетическая энергия молекул.

Термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул.

44. Закон равномерного распределения энергии по степеням свободы

Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковое количество кинетической энергии равной

Кинетическая энергия молекулы имеющая i-степеней свободы

Однозначной функции состояния идеального газа является его внутренняя энергия, она равна кинетической энергии молекул газа.

Внутренняя энергия одного моля идеального газа

В общем случае внутренняя энергия идеального газа

45. Классическая теория теплоёмкости идеального газа.

Классический статистический метод изучения тепловых свойств вещества позволил теоретически вычислить теплоёмкость газов и других тел.

В общем случае теплоёмкость

в изотермическом процессе не изменяется

Поэтому считается что в данном процессе изменение температуры = 0.

В адиабатном процессе система не получает и не отдаёт теплоту. Теплоёмкость = 0.

При изохорном процессе (v=const) молярная теплоёмкость при постоянном объёме.

- Закон Майера

С помощью данных процессов можно найти как общую теплоёмкость (для этого молярную теплоёмкость надо умножить на кол-во вещества m/M) и удельную теплоёмкость (молярную теплоёмкость разделить на молярную массу)

Классическая теория теплоёмкости газов приводит к расхождению с опытными данными.

1. Теплоёмкость от температуры не зависит. Это не ТАК! Опыт показывает что для всех веществ теплоёмкость растёт с увеличением температуры.

2. Занижена оценка теплоёмкости. Причина всех трудностей в ограниченной пригодности закона равномерного распределения энергии по степеням свободы. В квантовой теории теплоёмкости эти трудности преодолены.

46. Распределение Максвелла.

Молекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры Т. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а величины скоростей подчиняются определенной закономерности. Распределение молекул газа по величине скоростей называется распределением Максвелла.

Если одновременно измерить скорости большого числа N молекул газа и выделить некоторый малый интервал скоростей от v до v+ v, то в выделенный интервал  v попадает некоторое число  N молекул. На графике удобно изображать зависимость величины 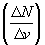  от скорости v. При достаточно большом числе N эта зависимость изображается плавной кривой, имеющей максимум при   (наиболее вероятная скорость). Здесь m - масса молекулы,  - постоянная Больцмана.

Характерным параметром распределения Максвелла является так называемая среднеквадратичная скорость   означает среднее значение квадрата скорости. В молекулярной физике доказывается, что

где  - молярная масса.

Из выражения для среднеквадратичной скорости следует, что средняя кинетическая энергия поступательного движения молекул газа есть

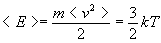
Распределение Максвелла является одной из важнейших статистических закономерностей молекулярной физики.