25.Парабола.

Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Обозначим фокус F, расстояние от фокуса до директрисы р. Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокус перпендикулярно директрисе в направлении от директрисы к фокусу и начало координат делило пополам расстояние между фокусом и директрисой (рис. 33). Тогда  а уравнение директрисы

 

 – каноническое уравнение параболы.

Уравнение содержит у лишь в четной степени, следовательно, кривая симметрична относительно оси ОХ. При х = 0 у = 0, то есть парабола проходит через начало координат. Из уравнения следует, что х ³ 0 – кривая располагается в правой полуплоскости. При х ® +¥ ôуô ® +¥ (рис. 34). Ось симметрии параболы называется ее фокальной осью, точка 0 – вершиной параболы.

Рис. 34

Замечание. При другом выборе системы координат получаются канонические уравнения другого вида (рис. 35, 36, 37).

 

х2=2ру

Рис. 35

у2=–2рх

Рис. 36

 

х2=–2ру

26.Поворот и параллельный перенос осей координат (на плоскости).

Параллельный перенос осей координат

Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от систе­мы координат Оху к новой системе О₁х₁у₁, при котором меняется поло­жение начала координат, а направление осей и масштаб остаются неиз­менными.

Пусть начало новой системы координат точка О₁ имеет координаты (х₀;y₀) в старой системе координат Оху, т. е. О₁ (х₀;y₀). Обозначим координаты произвольной точки Μ плоскости в системе Оху через (х;у), а в новой системе O₁x₁y₁ через (х';у') (см. рис. 28).

Рассмотрим векторы

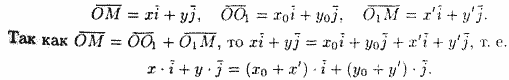
Следовательно,

Полученные формулы позволяют находить старые координаты x и у по известным новым х' и у' и наоборот.

Поворот осей координат

П од поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.

Пусть новая система O₁x₁y₁ получена поворотом системы Оху на угол α.

Пусть   Μ  произвольная   точка   плоскости, (х;у) — ее координаты в старой системе и (х';у') — в новой системе.

Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Οx₁ (масштаб одинаков). Полярный радиус r в обеих системах одинаков, а полярные углы соответственно равны α + j и φ, где φ — полярный угол в новой полярной системе.

По формулам перехода от полярных координат к прямоугольным имеем

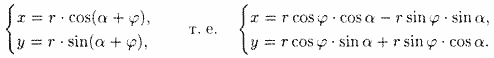
Но rcosj = х' и rsinφ = у'. Поэтому

Полученные формулы называются формулами поворота осей. Они позволяют определять старые координаты (х; у) произвольной точки Μ через новые координаты (х';у') этой же точки М, и наоборот.

Е сли новая система координат O₁x₁y₁ получена из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол α (см. рис. 30), то путем введения вспомогательной системы легко получить формулы

 

выражающие старые координаты х и у произвольной точки через ее новые координаты х' и у'.

27.Общее уравнение плоскости в пространстве (с доказательством). Уравнение плоскости, проходящей через данную точку с данной нормалью. Пусть М_о(х_о, у_о, z_о) – заданная точка в плоскости ,  = (А; В; С) – вектор, перпендикулярный плоскости , его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда    то есть

– уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

 

Раскрыв скобки и сгруппировав слагаемые, получим  Обозначим   уравнение примет вид

 

– общее уравнение плоскости.