Матрицей размера m x n называется прямоугольная таблица чисел, содержащая м строк и n столбцов. Числа, составляющие матрицу называются элементами матрицы.

Матрицы обозначаются прописными буквами латинского алфавита, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: a_ij , i – номер строки, j – номер столбца.

Две матрицы одного размера называются равными, если они совпадают поэлементно.

Виды матриц. М-ца состоящая из одной строки, называется м-цей строкой, а из одного столбца м-цей столбцом.

М-ца назыв. Квадратной n-го порядка, если число её строк равно числу её столбцов и равно n.

М-цы у кот. Номер столбца равен номеру строки, называют диагональными и образуют главную диагональ м-цы.

Операции над матрицами. Суммой двух матриц одинакового размера A=(a_ij) и B=(b_ij) называется матрица C, у которой (c_ij)=(a_ij+b_ij), и записывают C = A + B.

Произведением матрицы A=(a_ij) на число k называется такая матрица C=(c_ij), у которой (c_ij) = (ka_ij).

Если A=(a_ij)_m×p, а B=(b_ij)_p×n, то произведением матрицы A на матрицу B назовем матрицу C, каждый элемент которой вычисляют по формуле:

C = A·B = (a_ij)_m×p·(b_ij)_p×n=(a_s1b_1k+a_s2b_2k+...+a_skb_sk)_m×n=(c_ij)_m×n

Если AB = BA, то такие матрицы A и B называют перестановочными или коммутативными.(коммутирующими)(А и Аⁿ)

Если в некоторой матрице A поменять местами столбцы и строки, то полученная матрица будет называться транспонированной и обозначается A^т.

• (А^Т) ^Т=А

• (КА)^Т=КА^Т

• (А+В)^Т=А^Т+В^Т

• (АВ)^Т=В^ТА^Т

Если выполняется равенство A = A_т, то такая матрица называется симметрической.

2.Понятие определителя n-ого порядка. Схемы вычисления определителей 2-ого и 3-ого порядков

Понятие определителя n-ого порядка. Определителем квадратной матрицы n-ого порядка называется число, равное алгебраической сумме n членов, каждый из которых является произведением n-элементов матрицы, взятых по одному из каждой строки или столбца (причём знак каждого члена определяется как (-1)r(j), где r(j)-число инверсий).

Инверсия- количество пар чисел в последовательности. среди которых большее стоит перед меньшем.

Например: в числе 3 475 693 количество инверсий =7 (43,75,76,73,53,63,93)

Определителем второго порядка

 называется определителем 2-го порядка.

Числа  – это элементы определителя. Определитель 2-го порядка имеет две строки и два столбца. Индексы, стоящие внизу соответствующего элемента, означают номер строки и номер столбца определителя, на пересечении которых стоит указанный элемент. Например, элемент  стоит в первой строке и втором столбце определителя.

Элементы называют элементами главной диагонали определителя, а другие два элемента – соответственно элементами побочной диагонали.

Пример 1. Вычислим определитель

.

1.2. Определители 3-го порядка

Определение. Выражение

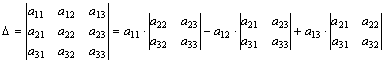(1.1)

называется определителем 3-го порядка.

Пример 2. Вычислить определитель:

.

Решение. По определению получим:

Если в формуле (1.1) раскрыть определители 2-го порядка и собрать слагаемые с одинаковыми знаками, то имеем:

       (1.2)

Элементы со знаком плюс и со знаком минус выбираются из определителя, как показано на рисунке:

+

-

 

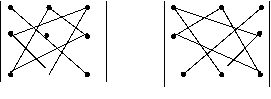
Этот способ вычисления определителя 3-го порядка называется правилом треугольника.

3.Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя.

Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n-го порядка, определитель которой Δk называется минором k–го порядка матрицы A.

Пример. Выписать три минора второго порядка матрицы

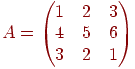
Решение.

Алгебраическое дополнение.

Алгебраическим дополнением А_ij для элемента квадратной матрицы а_ij называется минор этого элемента, взятый со знаком (-1)^i+j .

Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов к.-л. строки или столбца на их алгебраические дополнения.

Доказывается на примере.

Теорема разложения. Определитель 3-го порядка равен сумме парных произведений элементов какого-либо ряда определителя на их алгебраические дополнения (под рядом понимается строка или столбец).

Таким образом, имеет место шесть разложений:

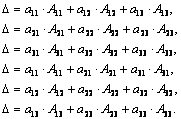                             (1.4)

Можно доказать, что сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения элементов параллельного ряда равна нулю.

Пример 4. Вычислить определитель

,

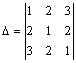разлагая его по элементам второй строки.

Решение. Согласно теореме разложения имеем:

.