47.Задача о скорости неравномерного прямолинейного движения.

Задача о скорости движения. Рассмотрим уравнение неравномерного прямолинейного движения S=¦(t), определенного на множестве (a,b). Зафиксируем последовательно два момента времени t₀ и t ₁ Î(a,b) и обозначим  D t =t₁ - t₀.

Средней скоростью движения, соответствующей некоторому промежутку времени t, называется отношение пройденного пути, за этот промежуток времени

                                                     

Средняя скорость не характеризует движение в каждый момент времени. Для того чтобы найти скорость в данный момент t₀, необходимо уменьшить промежуток времени t=t₁-t₀. Чем меньше промежуток , тем меньше средняя скорость отличается от скорости в данный момент времени, т. е. от мгновенной, точное значение скорости  равно пределу  при , т. е.   

.                                            

48.Задача о касательной, приводящая к понятию о производной.

Пусть на множестве (a, b) задана функция y=¦(x). Отметили в декартовой ee системе координат XOY график в виде кривой К x₀;

Возьмем две точки М₀ (¦(x₀)) и М₁(x₁;¦(x₁)) и проведем через них секущую М₀ М₁, ее угол наклона обозначим через a₁. Тогда, если точка М₁, двигаясь по кривой будет приближаться к точке М₀, положение секущей изменяется.

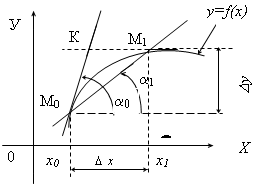
Рис. 2.17. К задаче о секущей

Когда точка М₁ совместиться с М₀, секущая превратиться в касательную. В этом случае a₁=a₀, где a₀ - угол наклона касательной.

Из рисунка видно, что

                       

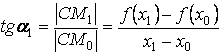
т.к. x₁-x₀=D x- это приращение аргумента, ¦(x₁)-¦(x₀)=D y - приращение функции, то

tga₁=                                                      (2-69)

Осуществляя предельный переход, когда М₁ М₀

.               

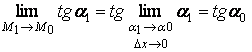Учитывая (2-69), имеем

.                             

Итак, тангенс угла наклона касательной , равен пределу отношения приращения функции к приращению аргумента, когда последнее, равно нулю.

Тангенс угла наклона касательной показывает, во сколько раз быстрее изменяется функция по сравнению с изменением аргумента в точке касания, т.е. характеризует скорость процесса или явления, описываемого кривой К. Зная тангенсы углов наклона касательной к графику функции в двух различных точках, можно сравнивать ’’крутизну подъема’’ графика. Так в точке (x₀,f(x₀)) (см. рис.) касательная расположена ''круто'', т. е. тангенс угла наклона большой, функция изменяется быстро, тогда как в точке (x₁,f(x₁)) тангенс угла наклона касательной мал, функция изменяется медленно.

В точках, где касательная горизонта (tg =0), изменение функции почти не происходит.

Если касательная к графику функции в некоторой точке ^ к оси OX, то функция изменяется с бесконечно большой скоростью.

49.Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции. Примеры недифференцируемых функций в точке.

Основные понятия

 Пусть дана функция y = f(x). Рассмотрим два значения ее аргумента: исходное х₀ и новое х. Разности х = х-х₀ и  y = f(x)-f(x₀) = y-y₀ называются соответ­ственно приращением аргумента и приращением функции в точке х₀. Оче­видно, что х = х₀+х, у = у₀+у, у = f(x₀+x)-f(x₀). В дальнейшем будем считать значение х₀ фиксированным, а х – переменным. При этом х и у являются пе­ременными величинами. Производной функции у = f(x) в точке х₀ называется  если этот предел существует. Производная обозначается у'(x₀) или f'(x₀). Таким образом, .

Пусть Х = {х}-множество всех таких х, для которых существует y'(х). Очевидно, что (х) является функцией, определенной на множестве Х.

Нахождение производной функции называется дифференцированием этой функции. Функция, имеющая производную в точке х₀, называется дифференци­руемой в этой точке. Функция, дифференцируемая в каждой точке интервала (a, b), называется дифференцируемой на интервале (a, b). Геометрический смысл производной. Пусть функция у = f(x) дифференцируема в точке х₀, тогда угловой коэффициент касательной к графику функции, проведенной в точке (х₀, f(х₀)) равен у'(х₀). Физический смысл производной. Пусть материальная точка движется прямолинейно неравномерно по закону S = f(t), где t – время, S – путь, проходимый точкой за время t. Тогда скорость точки в момент времени t равна: V = S'(t). Теорема (о связи дифференцируемости и непрерывности). Если функция у = f(x) дифференцируема в точке х₀, то она непрерывна в этой точке. Доказательство. Пусть аргумент х получает в точке х₀ приращение х  0. Ему соответствует некоторое приращение функции у. Вычислим предел:

а это и означает непрерывность функции в точке х₀. Заметим, что обратная теорема неверна: существуют непрерывные функции, которые в некоторых точках не дифференцируемы. Примерами могут слу­жить функции у = х и  в точке х = 0. В обоих случаях (0) не существует.

Заметим, что график у = х в точке х = 0 не имеет касательной, а график  в точке х=0 имеет вертикальную касательную – ось Оу.

Можно показать, что для того, чтобы функция у = f(x) была дифференцируемой в точке х₀, необходимо и достаточно, чтобы ее график имел невертикаль­ную касательную в точке (х₀, f(х₀)).

В силу существования производной функции f в точке x₀, переходя к пределу при получаем, что существует предел

а в силу непрерывности арктангенса и предельный угол

Прямая, проходящая через точку (x₀,f(x₀)) и имеющая предельный угол наклона, удовлетворяющий задаётся уравнением касательной:

y = f(x₀) + f'(x₀)(x − x₀).

Пусть функция определена в некоторой окрестности точки , и дифференцируема в ней: . Касательной прямой к графику функции f в точке x₀ называется график линейной функции, задаваемой уравнением

• Если функция f имеет в точке x₀ бесконечную производную 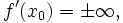то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением

x = x₀.