4.Свойства определителей. Вычисление определителей порядка выше 3-его при помощи свойств определителя и теоремы о разложении определителя.

Определитель- число, характеризующее матрицу. Определителем матрицы 1-го порядка А=(а₁₁)  является единственный элемент этой матрицы

. Свойства определителей.1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то Ñ этой матрицы равен 0. 2)При транспонировании матрицы её определитель не изменяется 3) Если все элементы к.-л. строки или столбца матрицы умножить на одно и то же число, то и det этой матрицы умножится на это же число. 4) При перестановке местами 2-х строк или столбцов матрицы её определитель меняет свой знак на противоположный. 5) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0. 6)Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0. 7) Определитель матрицы не изменяется если к элементам одной строки или столбца прибавить элементы другой строки или столбца, умноженный на одно и то же число.

Определение. Выражение

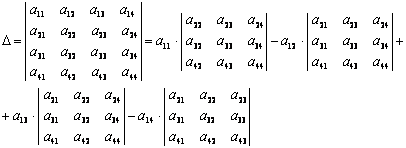
называется определителем 4-го порядка. Этот определитель можно записать в виде: ,      (1.6) где – это минор элемента, стоящего на пересечении i-ой строки, j-го столбца,  – его алгебраическое дополнение.

Формулу (1.6) можно записать короче с помощью значка суммирования S: , где                 (1.7)

Формула (1.7) называется разложением определителя по i-й строке. Можно записать и разложение определителя по j-му столбцу:

                                     (1.8)

Ясно, что формулы (1.7) и (1.8) значительно упрощаются, если все элементы строки или столбца за исключением одного равны нулю.

Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов определителя в нуль с помощью свойств определителей.

Метод приведения к треугольному виду заключается в таком преобразовании данного определителя, когда все элементы его, лежащие по одну сторону одной из его диагоналей, становятся равными нулю.

Пример 8. Вычислить определитель

 приведением к треугольному виду.

Решение. Вычтем первую строку определителя из остальных его строк. Тогда получим

.

Этот определитель равен произведению элементов главной диагонали. Таким образом, имеем

5.Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Алгоритм вычисления обратной матрицы.

Матрица А-1  называется обратной по отношению к квадратной матрице А, если при умножении её на заданную как справа так и слева получатся единичная матрица.

Теорема (необходимое и достаточн.условие сущ-я обратн.матрицы):  обратная матрица А-1  сущ-т и единственна тогда и только тогда, когда заданная матрица не вырожденная.

Матрица называется вырожденной, если её определитель равен 0, в противном случае она – не вырожденная.

Алгоритм:

1)Определитель заданной матрицы.

2)Транспонирование.

3)Алгебраические дополнения всех элементов транспонированной матрицы.

4) Присоед.матрица А@ (на месте каждого эл-та А^т  его алгебраич.доп-я)

. 5) А^-1= 1/DА *A@

. 6) Проверка=>А^-1  *А=Е.

Свойства:

1. IAI^-1=1/IAI

2. (A^-1)^T=(A^T)^-1

3. (AB)^-1=B^-1A^-1

4. (KA)^-1=1/K*A^-1