1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Векторная форма (2-й закон Ньютона):

Координатная форма (2-й закон Ньютона в проекциях на оси декартовых координат):

Естественная (эйлерова) форма (2-й закон Ньютона в проекциях на оси естественных координат):

где х, у, z - координаты точки массой m; X, Y, Z - проекции действующей на точку силы (или равнодействующей действующих на точку сил)   на оси декартовых координат;  - проекции силы   на оси естественных координат: касательную Т, главную нормаль N и бинормаль В (см. рис. 1).

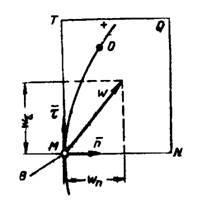
Рисунок 1.

Если точка является несвободной (на движение точки наложены связи), в число действующих на точку сил включаются реакции связей.

Силы, входящие в правую часть дифференциальных уравнений движения, в общем случае могут являться функциями от времени t, скорости v и координат х, у, z точки.

2.

Векторное поле. Если каждой точке  пространства ставится в соответствие вектор  , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде:  . Скалярные функции  однозначно определяют векторное поле. Векторное поле может быть плоским, если  , сферическим, когда  ,  , цилиндрическим, когда  ,  .

Изменение координат вектора при изменении базиса

Пусть в   -мерном линейном пространстве   выбран базис   , который мы будем для удобства называть "старый" и другой базис   , который мы будем называть "новый". Возьмем призвольный вектор   из   . Его координатный столбец в старом базисе обозначим   , а в новом -- 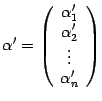  . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

3. Тензорное исчисление, математическая теория, изучающая величины особого рода — тензоры, их свойства и правила действий над ними.Тензорное исчисление является развитием и обобщением векторного исчисления и теории матриц. Величины, называемые тензорными, описываются в каждой системе координат несколькими числами (компонентами тензора), причём закон преобразования этих чисел при переходе от одной системы координат к другой более сложен, чем для векторов (точные определения будут даны ниже). При введении координатной системы, помимо чисел, описывающих сам объект или физическое явление, появляются числа, описывающие его связь с выбранной системой координат.

Примеры

• Тензор нулевого ранга — это скаляр;

• Один раз контравариантный тензор (ранга (0,1)) — это просто элемент пространства V, то есть вектор;

• Тензор ранга (1,0) есть ковектор (ковариантный вектор), то есть элемент пространства V ^*(или линейный функционал на V, 1-форма);

• Тензор ранга (2,0) есть билинейная форма, например метрический тензор gij

• Тензор ранга (1,1) есть линейный оператор 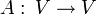  или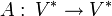 

• Форма объёма на n-мерном линейном пространстве есть пример антисимметрического тензора ранга (0,n) (или n раз ковариантного)

Базис и разложение по базису

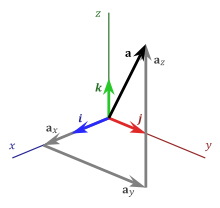
Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства

Векторы (как направленные отрезки), лежащие на прямых, параллельных одной прямой, называются коллинеарными, а векторы, лежащие в плоскостях, параллельных одной плоскости — компланарными. Для свободных векторов коллинеарность и компланарность определяется как такие понятия для изображающих их направленных отрезков (то есть представителей соответствующих свободным векторам классов эквивалентности).

Каждый вектор плоскости можно единственным образом разложить по двум определённым неколлинеарным векторам этой плоскости, а каждый вектор трёхмерного евклидова пространства можно единственным образом разложить по трём определённым некомпланарным векторам. Эти векторы, взятые в определённом порядке называются базисом плоскости (пространства). Сопоставлением каждому вектору данной плоскости (пространства) его коэффициентов в таком его разложении, определяется аффинная система координат на плоскости (в пространстве). Если векторы, по которым производится разложение, ортогональны и единичны, то получаем прямоугольную декартову систему координат на плоскости (в пространстве). Разложение геометрического вектора по базису есть упорядоченная совокупность проекций вектора на базисные вектора.

4. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

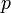•  — давление,

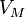•  — молярный объём,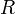

•  — универсальная газовая постоянная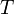

•  — абсолютная температура,К.

Так как  , где   — количество вещества, а  , где   — масса,   — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδQ, полученного телом, к соответствующему приращению его температуры δT:

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).

5.

Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.

Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. 

Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы.

Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). 

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).