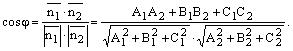- •2.Понятие определителя n-ого порядка. Схемы вычисления определителей 2-ого и 3-ого порядков
- •3.Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя.
- •4.Свойства определителей. Вычисление определителей порядка выше 3-его при помощи свойств определителя и теоремы о разложении определителя.
- •5.Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Алгоритм вычисления обратной матрицы.
- •6.Ранг матрицы. Преобразования матрицы, не меняющие ее ранга.
- •7.Системы m линейных уравнений с n неизвестными. Основные понятия. Матричный вид системы линейных уравнений.
- •8.Системы n линейных уравнений с n неизвестными. Метод обратной матрицы.
- •9.Системы линейных уравнений с n неизвестными.Формулы Крамера.
- •10.Метод Гаусса решения системы m линейных уравнений с n неизвестными.
- •12.Системы линейных однородных уравнений. Существование ненулевого решения.
- •15.Скалярное произведение векторов и его свойства.Условие перпендикулярности векторов.Угол между векторами.
- •16.Векторное произведение и его свойства.
- •17.Смешанное произведение и его свойства.Условие компланарности векторов.
- •18.Общее уравнение прямой на плоскости. Случаи расположения прямой относительно осей координат.Уравнение прямой в отрезках.
- •19.Уравнение прямой с угловым коэффициентом.Уравнение прямой, проходящей через данную точку в данном направлении.
- •20.Уравнение прямой, проходящей через две данные точки (на плоскости).
- •21.Угол между двумя прямыми (на плоскости). Условия параллельности и перпендикулярности прямых.
- •22.Расстояние от точки до прямой.
- •23.Эллипс
- •24.Гипербола.
- •25.Парабола.
- •26.Поворот и параллельный перенос осей координат (на плоскости).
- •28.Случаи расположения плоскости относительно осей координат.Уравнение плоскости в отрезках.
- •29.Условие параллельности и перпендикулярности плоскостей. Угол между плоскостями.
- •30.Уравнение прямой в пространстве,как линии пересечения двух плоскостей. Канонические уравнения прямой в пространстве.
- •31.Уравнения прямой в пространстве, проходящей через две данные точки. Параметрические уравнения прямой в пространстве.
- •33.Предел числовой последовательности.
- •34.Предел функции на бесконечности.
- •32.Угол между прямой и плоскостью
- •35.Предел функции в точке.
- •36.Бесконечно малые функции. Связь бесконечно малой функции и функции, имеющей предел.Свойства бесконечно малых функций.
- •37.Бесконечно большие функции.Их свойства.Теорема о связи бесконечно большой и бесконечно малой функций.
- •38.Теорема о единственности предела.Основные теоремы о пределах.Предел сложной функции.
- •Теорема о пределе сложной функции.
- •39.Признаки существования пределов.
- •Теорема о сохранении функцией знака своего предела
- •40.Первый замечательный предел.
- •41. Сравнение бесконечно малых функций. Примеры эквивалентных бесконечно малых функций.
- •42.Второй замечательный предел.Число е.Важные пределы как следствие второго замечательного предела.
- •43.Задача о непрерывном начислении процентов.
- •44.Непрерывность функции в точке.Приращение функции,приращение аргумента.Свойства функций, непрерывных в точке.
- •45.Непрерывность функции на отрезке.
- •46.Классификация точек разрыва.
- •47.Задача о скорости неравномерного прямолинейного движения.
- •48.Задача о касательной, приводящая к понятию о производной.
- •49.Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции. Примеры недифференцируемых функций в точке.
- •Замечание
- •54.Производная степенной функции. Логарифмическая производная.
- •55.Производные высших порядков.
28.Случаи расположения плоскости относительно осей координат.Уравнение плоскости в отрезках.
Если в этом уравнении А, В, С, Д 0, то его можно привести к виду
![]()
-уравнение плоскости в отрезках (аналогично (2.14)). Здесь а, в, с – отрезки, отсекаемые плоскостью на осях координат.
Неполные уравнения плоскостей
Если
в уравнении плоскости
![]() какие-либо
из коэффициентов равны нулю, то получится
неполное уравнение плоскости.
какие-либо
из коэффициентов равны нулю, то получится
неполное уравнение плоскости.
Пусть,
например,
![]() Уравнение
имеет вид
Уравнение
имеет вид
![]() и
определяет плоскость, проходящую через
начало координат (координаты точки
О(0; 0; 0) удовлетворяют уравнению).
и
определяет плоскость, проходящую через
начало координат (координаты точки
О(0; 0; 0) удовлетворяют уравнению).
Пусть
![]() Уравнение
имеет вид
Уравнение
имеет вид
![]() и
определяет плоскость, параллельную
оси Оz
или проходящую через ось Оz
при
Действительно,
тогда
и
определяет плоскость, параллельную
оси Оz
или проходящую через ось Оz
при
Действительно,
тогда
![]() то
есть
то
есть
![]() а
плоскость
а
плоскость
![]()
Пусть
![]() Уравнение
имеет вид
Уравнение
имеет вид
![]() и
определяет плоскость, параллельную
плоскости Оуz
или совпадающую с ней при
Действительно,
и
определяет плоскость, параллельную
плоскости Оуz
или совпадающую с ней при
Действительно,
![]() то
есть
то
есть
![]() а
плоскость
а
плоскость
![]() или
или
![]()
Аналогично можно рассмотреть другие случаи.
29.Условие параллельности и перпендикулярности плоскостей. Угол между плоскостями.
Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноимённых переменных
Если
![]() то
то
![]() –
условие параллельности плоскостей.
–
условие параллельности плоскостей.
Если
![]() то
то
![]() то
есть
то
есть
![]() –
условие перпендикулярности плоскостей.
–
условие перпендикулярности плоскостей.
Пусть
плоскости 1
и 2
заданы соответственно уравнениями
![]()
![]() где
где
![]()
![]() и
и
![]() –
нормальные векторы этих плоскостей
(рис. 45). Очевидно,
–
нормальные векторы этих плоскостей
(рис. 45). Очевидно,
![]() тогда
косинус угла между плоскостями
тогда
косинус угла между плоскостями
|
(2.32) |
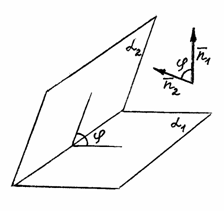
Рис. 45
30.Уравнение прямой в пространстве,как линии пересечения двух плоскостей. Канонические уравнения прямой в пространстве.
Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как мн-во точек, удовлетворяющих системе
![]()
![]()
Это можно назвать общим видом прямой в пространстве.
Направляющий
вектор прямой (2.37) можно найти как
векторное произведение нормальных
векторов пересекающихся плоскостей:
![]()
. Прямую в пространстве можно задать уравнениями, аналогичными уравнениям прямой на плоскости.
|
(2.34) |
– канонические уравнения, здесь хо, уо, zо – координаты заданной точки на прямой, а m, n, p – координаты направляющего вектора прямой (вектора, параллельного прямой);
31.Уравнения прямой в пространстве, проходящей через две данные точки. Параметрические уравнения прямой в пространстве.
|
(2.35) |
– параметрические уравнения прямой;
|
(2.36) |
– уравнения прямой, проходящей через две данные точки М1(х1, у1, z1) и М2(х2, у2, z2).
33.Предел числовой последовательности.
Пусть
дано топологическое
пространство
![]() и
последовательность
и
последовательность
![]() .
Тогда, если существует элемент
.
Тогда, если существует элемент
![]() такой,
что
такой,
что
![]() ,
,
где
![]() —
открытое множество, содержащее
—
открытое множество, содержащее
![]() ,
то он называется пределом последовательности
.
Если пространство является метрическим,
то предел можно определить с помощью
метрики: если существует элемент
такой,
что
,
то он называется пределом последовательности
.
Если пространство является метрическим,
то предел можно определить с помощью
метрики: если существует элемент
такой,
что
![]() ,
,
где
![]() —
метрика, то
называется
пределом
.
—
метрика, то
называется
пределом
.
Не
у всякой последовательности существует
предел. Например, если взять в качестве
пространства множество вещественных
чисел
со стандартной топологией, а в качестве
последовательность
![]() ,
то у неё не будет предела. Если у
последовательности существует предел,
то она называется сходящейся,
если нет — расходящейся
,
то у неё не будет предела. Если у
последовательности существует предел,
то она называется сходящейся,
если нет — расходящейся